Carl Friedrich Gauss
Durante il periodo della Rivoluzione, i matematici più importanti erano francesi, ma nel XIX secolo, altri paesi iniziarono a emergere in campo matematico. Carl Friedrich Gauss (1777-1855), un matematico tedesco considerato uno dei più grandi di tutti i tempi, non lasciò mai la Germania. Gauss mostrò il suo talento fin da giovane, nonostante le difficoltà dell'ambiente familiare. Sua madre lo incoraggiò negli studi, mentre suo padre, un operaio, cercò di impedirgli di ricevere un'educazione adeguata.
Frequentò la scuola locale e dimostrò le sue abilità in matematica in varie occasioni. A 15 anni, grazie alle raccomandazioni del Duca di Braunschweig, Gauss entrò nel collegio di Braunschweig e nel 1795 si iscrisse all'università di Gottinga. All'inizio, era indeciso se studiare teologia o matematica, ma alla fine scelse la matematica. Nel 1796 fece una scoperta importante: costruì il poligono regolare di 17 lati usando solo riga e compasso, secondo le regole euclidee.
Gauss fu legato per tutta la sua vita alla figura del poligono regolare di 17 lati. Al punto da volerlo come un sigillo inciso sulla sua pietra tombale. Il suo desiderio non venne però soddisfatto, in quanto il poligono regolare di 17 lati poteva essere scambiato per un cerchio. In un altro monumento dedicato Gauss a Braunschweig è però presente.
Gauss iniziò a tenere un diario in cui annotava le sue maggiori scoperte, tra cui quella del poligono regolare di 17 lati. Il diario, composto da soli 19 pagine, è considerato uno dei documenti più preziosi nella storia della matematica. In esso sono elencati 146 risultati brevemente formulati. Il diario ci permette di tracciare lo sviluppo del suo genio e di verificare la priorità delle sue scoperte in caso di rivendicazioni da parte di altri matematici. Tuttavia, Gauss era riluttante a pubblicare le sue idee. Pertanto, il diario rimase nascosto fino al 1898, quando fu scoperto tra le carte di famiglia e successivamente pubblicato nel 1901 dal matematico Felix Klein.
Gauss studiò anche all'Università di Helmstädt per un po', dove ottenne il dottorato nel 1798. La sua tesi dimostrava un teorema fondamentale dell'algebra, simile a quello di d'Alembert in Francia, in base al quale affermava che "ogni funzione razionale intera a una variabile può essere risolta in fattori reali di primo o secondo grado". Nella tesi Gauss mostrò anche come le dimostrazioni precedenti, incluse quelle di Eulero e Lagrange, fossero inadeguate.
Un altro contributo di Gauss è la rappresentazione dei numeri complessi sul piano, conosciuto anche come "Piano di Gauss".
Nota. In realtà, la rappresentazione grafica dei numeri complessi era stata scoperta nel 1797 da Caspar Wessel, ma il suo lavoro rimase quasi sconosciuto. Pertanto, l'interpretazione geometrica dei numeri complessi come punti di un piano è spesso chiamata "piano di Gauss", anche se Gauss pubblicò i suoi risultati molto tempo dopo rispetto a Wessel.
Era noto che i numeri reali potevano essere rappresentati come punti su una retta, e alcuni avevano suggerito di rappresentare numeri immaginari puri con una retta perpendicolare all'asse dei numeri reali. Tuttavia, nessuno prima di Wessel e Gauss aveva pensato di usare la parte reale e immaginaria di un numero complesso come coordinate ortogonali dei punti di un piano.
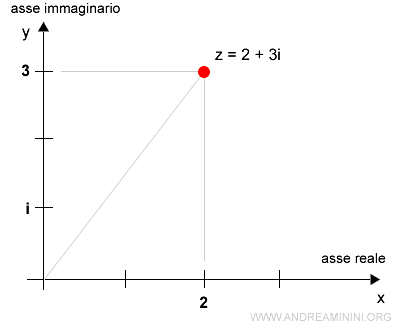
Ad esempio, il numero complesso z=2+3i posso rappresentarlo come un punto del piano alle coordinate (2;3) poiché la sua parte reale è uguale a 2 e quella immaginaria è uguale a 3.
Questo diede ai matematici maggiore confidenza con i numeri immaginari, poiché ora potevano essere visualizzati in modo tale che ogni punto del piano corrispondesse a un numero complesso e viceversa. La maggior parte dei matematici abbandonò le vecchie idee sulla non esistenza dei numeri immaginari.
La tesi di dottorato di Gauss dimostrava che ogni equazione polinomiale f(x)=0 ha almeno una radice, sia che i coefficienti siano reali o immaginari. Senza entrare nei dettagli, Gauss ha risolto un'equazione complessa utilizzando un grafico e separando le parti reali e immaginarie dell'equazione. Graficamente, ha mostrato l'intersezione tra due curve, che rappresentano una soluzione dell'equazione. Questo dimostra che ogni equazione polinomiale ha almeno una radice complessa.
Gauss ha usato questo risultato per dimostrare che ogni polinomio di una variabile può essere scomposto nel prodotto di fattori reali di primo o secondo grado. La sua dimostrazione si basava in parte su considerazioni geometriche. Gauss ha successivamente pubblicato altre dimostrazioni nel tentativo di dimostrarlo con metodi puramente algebrici.
Due anni dopo la pubblicazione della sua tesi di dottorato, Gauss pubblicò il suo lavoro più famoso, un trattato in latino sulla teoria dei numeri chiamato "Disquisitiones Arithmeticae". Inizialmente aveva intenzione di pubblicare due volumi delle Disquisitiones, ma scrisse solo il primo. Quest'opera è principalmente fornisce lo sviluppo della terminologia e della notazione dell'algebra delle congruenze e un primo esempio di classi di equivalenza.
Gauss introdusse il concetto di congruenza tra numeri:
Se un numero "a" divide la differenza tra due numeri "b" e "c", questi numeri si dicono congrui, altrimenti incongrui. Il numero "a" viene chiamato modulo. La notazione usata da Gauss, tuttora in uso, è b ≡ c (mod a).
Gauss costruì un' algebra basata sulla relazione di congruenza, simile all'algebra comune basata sull'uguaglianza. La relazione di congruenza ha alcune proprietà simili all'uguaglianza, come la riflessività, simmetria e transitività. In altre parole, sia l'uguaglianza che la congruenza sono relazioni di equivalenza.
Nota. Tuttavia, alcune regole dell'algebra ordinaria non valgono per le congruenze. Ad esempio, nella congruenza, la legge di eliminazione e la regola per l'equazione lineare valgono solo se il modulo e i numeri interi coinvolti non hanno fattori comuni.
In seguito, Gauss cercò di formulare teoremi per congruenze specifiche, ma per farlo dovette estendere il concetto di "intero" ai numeri complessi interi, come a + bi, dove a e b sono interi. Questi numeri sono anche conosciuti come "numeri interi gaussiani" e formano un campo di numeri simile a quello dei numeri interi reali, ma più generale e complicato. In quest'ambito Gauss scrisse il teorema fondamentale dell'aritmetica, un principio fondamentale valido anche per i numeri interi gaussiani.
Gauss dimostrò interesse anche per i numeri primi, come molti altri matematici. Ad esempio, annotò a mano la formula n/ln(n) sulla copertina di un suo manuale. Questa formula è l'enunciato dei numeri primi in base al quale il numero di numeri primi di un numero intero "n" si avvicina asitntoticamente al quoziente n/ln(n) quando a cresce indefinitivamente. Tuttavia, Gauss non andò oltre, non condivise questo appunto e non aggiunse nemmeno alcuna una dimostrazione a riguardo.
Successivamente Gauss si concentrò su altri interessi come l'astronomia e la statistica.
Nota. All'inizio del XIX secolo, fu scoperto l'asteroide Cerere, che andò poi perso. Gauss, conscio delle sue abilità nel calcolo, utilizzò il metodo dei minimi quadrati per determinare l'orbita di Cerere basandosi sulle osservazioni disponibili. Il suo metodo, ancora in uso oggi, ebbe successo e Cerere fu ritrovato.
La sua fama crebbe sia in matematica che in astronomia, e nel 1807 divenne direttore dell'Osservatorio di Gottinga. Pur lavorando presso l'osservatorio, Gauss continuò a contribuire alla matematica.
Gauss non pubblicò sempre le sue scoperte, quindi spesso altri matematici scoprivano cose che lui aveva già trovato. Ad esempio, in alcuni appunti Gauss aveva scoperto la doppia periodicità delle funzioni ellittiche ma non li pubblicò. Pertanto, questa scoperta è attributa ai matematici Abel e Jacobi.
