La conservativitÓ nelle reti di Petri
Nello studio della conservatività di una rete di Petri bisogna distinguere i concetti di rete conservativa e rete strettamente conservativa.
La rete conservativa
Una rete marcata <N,M0> di Petri è detta conservativa se conserva le proprie risorse (marche), ossia se esiste un vettore peso W composto da numeri interi positivi $$ W = [ w_1, w_2, ... w_p ] \ge 0 $$ tale che per ogni marcatura raggiungibile M dell'insieme di raggiungibilità R(N,M0) è soddisfatta l'equazione $$ W^T \cdot M = W^T \cdot M_0 $$
La precedente equazione vuol dire che il numero delle marche pesato tramite il vettore W non cambia.
E' importante sottolineare che in una rete conservativa il numero delle marche può anche cambiare con gli scatti.
Nota. La conservatività è una proprietà legata alla limitatezza perché una rete conservativa è anche una rete limitata.
Esempio
Questa rete è conservativa
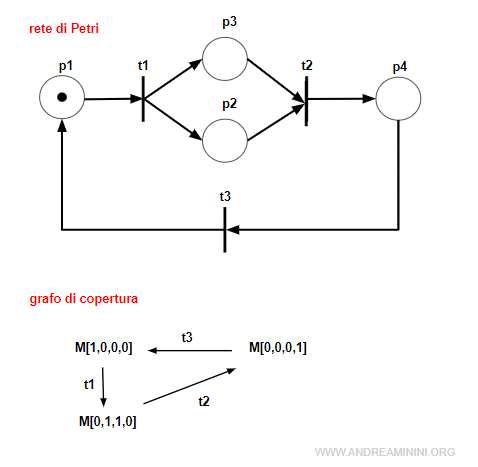
perché esiste un vettore W di interi positivi
$$ W = [ 2, 1, 1, 2 ] $$
tale che per ogni marcatura M raggiungibile il numero delle marche nel prodotto WTM non cambia.
$$ W^T·M_0 = [2,1,1,2]^T·[1,0,0,0] = [2,0,0,0] $$
$$ W^T·M = [2,1,1,2]^T·[0,1,1,0] = [0,1,1,0] $$
$$ W^T·M = [2,1,1,2]^T·[0,0,0,1] = [0,0,0,2] $$
In ogni marcatura raggiungibile M moltiplicata per il vettore trasposto WT ci sono sempre 2 marche.
Pertanto, la rete è conservativa.
La rete strettamente conservativa
Una rete marcata <N,M0> è strettamente conservativa se il numero delle marche è costante in ogni marcatura raggiungibile.
In questo caso la rete è conservativa con riferimento a un vettore peso composto da tutti gli elementi uguali a 1.
$$ W = [1, 1, ... , 1] $$
Per ogni marcatura raggiungibile M dell'insieme di raggiungibilità R(N,M0) è soddisfatta l'uguaglianza
$$ W^T \cdot M = W^T \cdot M_0 $$
Essendo i vettori unitari
$$ M = M_0 $$
ossia
$$ \sum_1^p M(p) = \sum_1^p M_0(p) $$
Quindi, il numero delle marche è sempre lo stesso.
Esempio
Questa rete è strettamente conservativa perché il numero delle marche non cambia.
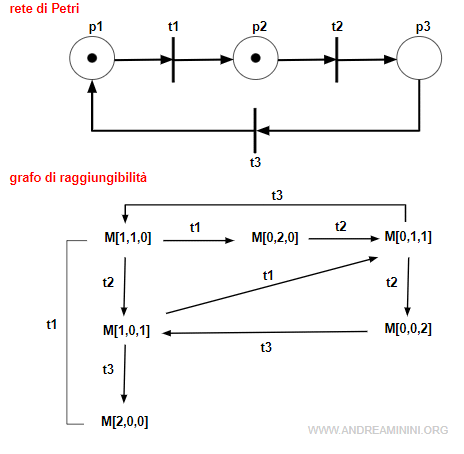
Ogni marcatura raggiungibile M dell'insieme di raggiungibilità R(N,M0) contiene due marche.
Cambia soltanto la disposizione delle marche nei posti.
Condizione sufficiente di stretta conservatività
Una condizione sufficiente (ma non necessaria) della stretta conservatività è l'uguaglianza del numero di archi in entrata e uscita per ogni transizione. $$ \sum_{p \in P} Pre(p,t) = \sum_{p \in P} Post(p,t) $$
Se ogni transizione della rete ha eguale numero di archi in entrata e uscita, il numero delle marche non può cambiare dopo qualsiasi scatto.
Questa condizione è sufficiente per dimostrare la stretta conservatività ma non necessaria.
Esempio. Una rete potrebbe avere una transizione con un diverso numero di archi pre e post. Se questa transizione però non scatta mai, la rete è comunque strettamente conservativa. Ad esempio, questa rete è strettamente conservativa anche se il posto p3 ha due archi in entrata e uno solo in uscita, perché la transizione t4 non potrà mai scattare.
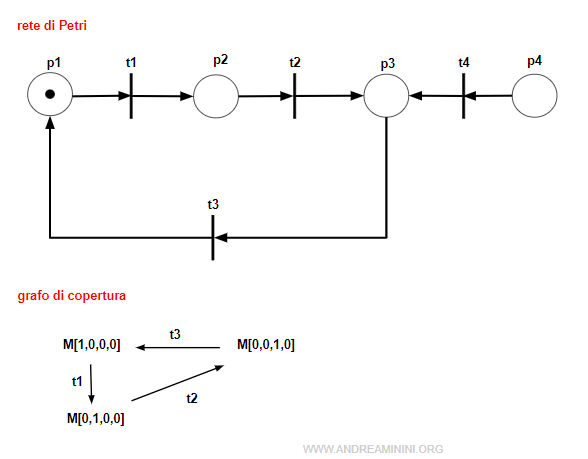
La conservazione e la limitatezza della rete
La proprietà di conservazione della rete è legata alla limitatezza.
Se una rete marcata <N,M0> è conservativa allora è anche una rete limitata.
Non vale però il contrario. Non tutte le reti limitate sono anche conservative.
Esempio. Questa rete è 1-limitata (sana) ma non è conservativa perché non esiste un vettore X (in questo caso il vettore ha un solo elemento, pertanto è un numero intero x) tale che XT·M = XT·M0.
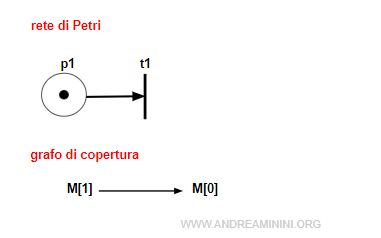
La rete ha due marcature raggiungibili [1] e [0] ma nessun numero intero x potrà mai soddisfare la seguente equazione $$ x \cdot [1] = x \cdot [0] $$ Quindi la rete non è conservativa.
Dimostrazione
Se una rete è conservativa, allora esiste un vettore W con elementi positivi tale che per ogni marcatura raggiungibile vale
$$ W^T \cdot M = W^T \cdot M_0 $$
dove W è un vettore composto da m elementi
$$ W = \sum_{i=1}^m w_i $$
Quindi
$$ W^T \cdot M = \sum_{i=1}^m w_i \cdot M(p_i) $$
Lo sostituisco alla precedente equazione
$$ W^T \cdot M = W^T \cdot M_0 $$
$$ \sum_{i=1}^m w_i \cdot M(p_i) = W^T \cdot M_0 $$
Ne consegue che per ogni valore di i vale
$$ w_i \cdot M(p_i) \le W^T \cdot M_0 $$
Metto in evidenza il numero di marche M(pi) del posto
$$ M(p_i) \le \frac{ W^T \cdot M_0 }{ w_i } $$
Questo dimostra che ogni posto pi della rete è k-limitato.
Con k uguale a
$$ k = \frac{ W^T \cdot M_0 }{ w_i } $$
Pertanto, una rete conservativa è anche strutturalmente limitata.
E così via.
