La reversibilità della rete di Petri

Cosa sono le reti reversibili

Una rete marcata <N,M₀> è detta rete reversibile se è possibile ritornare alla marcatura iniziale M₀ da qualsiasi altra marcatura raggiungibile M di R(N,M₀).

In pratica, la raggiungibilità è la capacità del sistema di tornare nello stato iniziale.

Per ogni sequenza di transizioni σ abilitata dalla marcatura iniziale M₀ esiste una sequenza σ' che riconduce alla marcatura M₀ da ogni marcatura raggiungibile della rete.

$$ M_0[σ>M $$

$$ M[σ'>M_0 $$

La sequenza di transizioni σσ' è detta sequenza stazionaria.

$$M_0[σσ'>M_0 $$

Nota. Se la rete è reversibile il sistema è stazionario, ossia non cambia stato.

Un esempio pratico

Esempio 1

Questa rete marcata è una rete reversibile perché da qualsiasi marcatura M è possibile tornare alla marcatura iniziale M₀=[1,0,0,0].

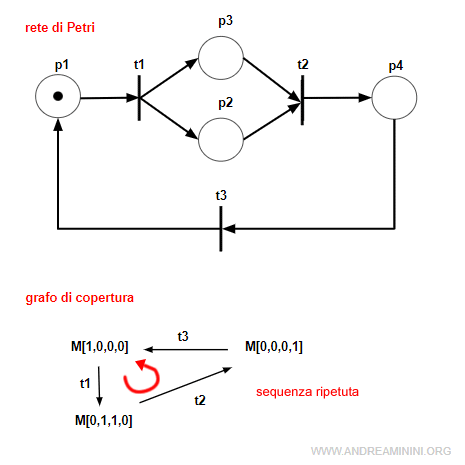
Esempio 2

Questa rete non è reversibile perché dalla marcatura M[0,0,1] non è possibile tornare alla marcatura iniziale M[1,0,0].

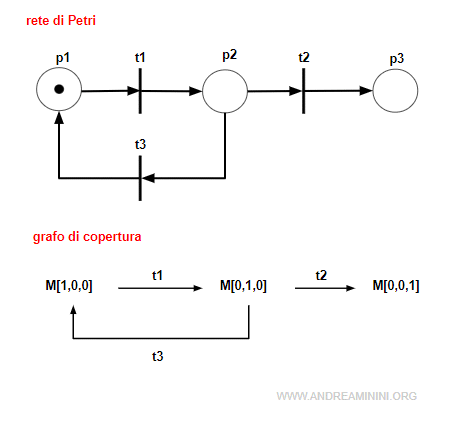
Quando scatta la transizione t₃ la marca si sposta nel posto p₃ e il sistema non può tornare in nessun modo alla marcatura iniziale M[1,0,0].

Nota. Soltanto dalla marcatura [0,1,0] è possibile tornare allo stato iniziale M[1,0,0], ossia dal posto p₂ tramite la transizione t₃, ma questo non è sufficiente a garantire la reversibilità della rete. Quindi, la presenza di alcune sequenze stazionarie non implica la reversibilità della rete.

La dimostrazione

Data una sequenza σ abilitata da M₀ che conduce alla marcatura raggiungibile M

$$ M_0[σ>M $$

Se esiste una sequenza σ' abilitata da M che riconduce a M₀

$$ M[σ'>M_0 $$

allora la sequenza σσ' è stazionaria.

$$ M_0[σσ'>M_0 $$

Se questo vale per ogni marcatura raggiungibile M, la rete è reversibile.

Nota. Da questo si deduce che, se la rete è revisibile allora esiste una transizione σ' tale che M[σ'>M₀ per ogni transizione σ abilitata da M₀ ossia M₀[σ>M.

Come riconoscere una rete reversibile

Se una rete è reversibile il grafo di raggiungibilità della rete è fortemente connesso.

In pratica, da qualsiasi marcatura raggiungibile esiste un cammino orientato che riconduce alla marcatura iniziale.

Si tratta di una condizione necessaria e sufficiente per la reversibilità.

Un esempio pratico

Questa rete è reversibile perché nel grafo di raggiungibilità è presente un cammino orientato verso la marcatura iniziale M₀=[1,1,0] da qualsiasi altra marcatura raggiungibile.

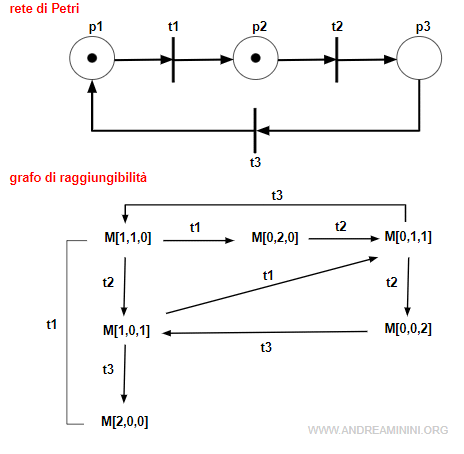
Ecco le transizioni di ritorno verso M[1,1,0]

• da M[0,2,0] la sequenza è t₂t₃ e altre
• da M[0,1,1] la sequenza è t₃ e altre
• da M[1,0,1] la sequenza è t₁t₃ , t₃t₁ e altre
• da M[0,0,2] la sequenza è t₃t₃t₁ e altre
• da M[2,0,0] la sequenza è t₃

Attenzione. E' necessario controllare la reversibilità sul grafo di raggiungibilità e non sul grafo di copertura. Il grafo di copertura permette soltanto un controllo sulle condizioni necessarie ma non sufficienti a garantire la reversibilità della rete. Ad esempio, in questa rete il grafo di copertura ha dei cammini orientati che rientrano in M₀. Tuttavia, lo scatto della transizione t₁ aumenta all'infinito le marche nel posto p₃. Pertanto, non si ottiene il ritorno alla marcatura M₀[1,0,0,0] bensì alla marcatura M₀[1,0,ω,0] che non è lo stato iniziale.

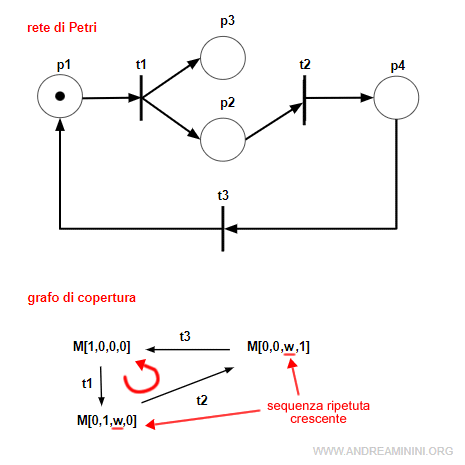
E così via.