Teorema del confronto tra topologie indotte da metriche

Siano $d$ e $d'$ due metriche su un insieme $X$, e siano $\mathcal{T}$ e $\mathcal{T}'$ le topologie indotte rispettivamente da $d$ e $d'$. Allora $\mathcal{T}'$ è più fine di $\mathcal{T}$ se e solo se per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste un $\delta > 0$ tale che: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ dove $B_{d}(x, \varepsilon)$ e $B_{d'}(x, \delta)$ sono intorni centrati in $x$ di raggio $\varepsilon$ e $\delta$, rispettivamente, nella metrica $d$ e $d'$.

In altre parole, se considero due modi diversi $d$ e $d'$ di misurare le distanze (metriche) in un insieme $X$, ogni metrica genera una topologia indotta, ovvero una collezione di insiemi aperti.

La topologia $\mathcal{T}$ per $d$
La topologia $\mathcal{T}'$ per $d'$

Il teorema stabilisce che la topologia $\mathcal{T}'$ è più fine di $\mathcal{T}$ (ossia $\mathcal{T}'$ ha più insiemi aperti) se e solo se ogni insieme aperto nella topologia indotta da $d$ contiene almeno un insieme aperto nella topologia indotta da $d'$.

Questa formulazione mette in evidenza la relazione tra le due topologie in modo più intuitivo e sottolinea la connessione tra metriche e insiemi aperti.

Un esempio pratico
La dimostrazione

Un esempio pratico

Considero l'insieme $X = \mathbb{R}^2$ dei punti del piano cartesiano con due metriche:

Metrica euclidea: $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$. Le palle in questa metrica sono cerchi, ossia: $$ B_d((x, y), \varepsilon) = \{(u, v) \in \mathbb{R}^2 : \sqrt{(u - x)^2 + (v - y)^2} < \varepsilon\} $$
Metrica discreta: $d'((x_1, y_1), (x_2, y_2)) = \begin{cases} 0 & \text{se } (x_1, y_1) = (x_2, y_2), \\ 1 & \text{se } (x_1, y_1) \neq (x_2, y_2) \end{cases}$ Le palle in questa metrica sono: \[ B_{d'}((x, y), \delta) = \begin{cases}
\{(x, y)\} & \text{se } \delta \leq 1, \\ X & \text{se } \delta > 1. \end{cases} \]

Voglio dimostrare che la topologia discreta è più fine della topologia euclidea.

Secondo il teorema:

$$ \mathcal{T}' \text{ è più fine di } \mathcal{T} \iff \forall x \in X, \forall \varepsilon > 0, \ \exists \ \delta > 0 \text{ tale che } B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

Prendo un generico punto $P = (x_0, y_0) \in \mathbb{R}^2$ e scelgo un raggio $\varepsilon > 0$ per la palla $B_d(P, \varepsilon)$ nella topologia euclidea.

La palla $B_d(P, \varepsilon)$ è un cerchio centrato in $ P = (x_0, y_0) $ di raggio $\varepsilon$.

Ora considero una open ball $B_{d'}(P, \delta)$ nella metrica discreta. Per definizione, questa palla è:

$\{P\}$ se $\delta \leq 1$,
$X$ (tutto lo spazio) se $\delta > 1$

In altre parole, nella topologia discreta ogni singolo punto è un insieme aperto.

Scelgo $\delta = 1$. In questo caso, $B_{d'}(P, \delta) = \{P\}$, che è chiaramente contenuto in $B_d(P, \varepsilon)$, perché $P \in B_d(x, \varepsilon)$.

Quindi, per ogni $ P = (x_0, y_0) $ e per ogni $\varepsilon > 0$, posso trovare un $\delta > 0$ tale che:

$$ B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon) $$

Ad esempio, considero il punto $P = (1, 2) \in \mathbb{R}^2$. Nella topologia euclidea, un intorno centrato in $P$ con raggio qualsiasi ( es. $\varepsilon = 0.4$ ) è un insieme aperto.
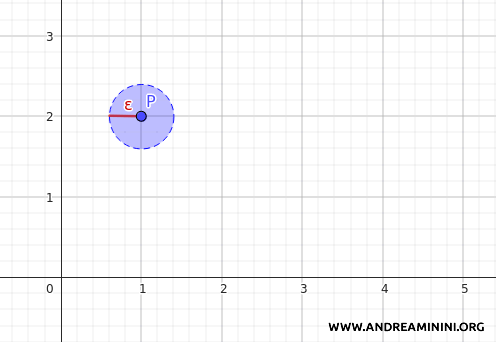
esempio
Nella topologia discreta, qualsiasi singolo punto è un insieme aperto. Quindi, $\{P\} = \{(1, 2)\}$ è un insieme aperto anche nella topologia discreta. Osservo che $\{P\} \subseteq B_d(P, \varepsilon)$, perché $P$ appartiene al cerchio $B_d(P, \varepsilon)$. Lo stesso esempio posso ripeterlo con qualsiasi altro punto del piano cartesiano. Questo conferma che ogni insieme aperto della topologia euclidea (come $B_d(P, \varepsilon)$) contiene almeno un insieme aperto della topologia discreta (come $\{P\}$).

In conclusione, ho verificato che la condizione del teorema è soddisfatta: la topologia discreta ($\mathcal{T}'$) è più fine della topologia euclidea ($\mathcal{T}$) perché, per ogni punto $P$ e ogni raggio $\varepsilon > 0$, esiste un $\delta > 0$ (in questo caso $\delta = 1$) tale che $B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon)$.

La dimostrazione

Devo dimostrare il teorema in entrambe le direzioni:

Se $\mathcal{T}'$ è più fine di $\mathcal{T}$, allora per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste $\delta > 0$ tale che $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$
Se per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste $\delta > 0$ tale che $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$, allora $\mathcal{T}'$ è più fine di $\mathcal{T}$.

Quindi, suddivido la dimostrazione in due parti:

A] Parte 1

Se la topologia $\mathcal{T}'$ è più fine di $\mathcal{T}$ allora $\implies$ per ogni $x \in X$ e $\varepsilon > 0$, esiste $\delta > 0$ tale che $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.

Per ipotesi iniziale $\mathcal{T}'$ è più fine di $\mathcal{T}$. Questo significa che ogni insieme aperto in $\mathcal{T}$ è aperto anche in $\mathcal{T}'$. In particolare, ogni open ball $B_d(x, \varepsilon)$ (che è aperta in $\mathcal{T}$) è anche aperta in $\mathcal{T}'$
Poiché $B_d(x, \varepsilon)$ è aperto in $\mathcal{T}'$ allora, per definizione di apertura, ogni punto $x$ in $B_d(x, \varepsilon)$ ha un intorno $B_{d'}(x, \delta)$ nella topologia di $d'$ che è contenuto interamente in $B_d(x, \varepsilon)$. Questo intorno è una open ball $B_{d'}(x, \delta)$ ossia un insieme aperto nella metrica $d'$.
Quindi, per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste un $\delta > 0$ tale che: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

B] Parte 2

Se per ogni $x \in X$ e $\varepsilon > 0$, esiste $\delta > 0$ tale che $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$ allora $\implies$ $\mathcal{T}'$ è più fine di $\mathcal{T}$.

Per ipotesi iniziale so che, per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste un $\delta > 0$ tale che: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$
Considero un insieme $U$ aperto nella topologia $\mathcal{T}$. Per definizione di insieme aperto, $U$ è l'unione di open ball $B_d(x, \varepsilon)$. Ora, voglio dimostrare che $U$ è anche aperto in $\mathcal{T}'$.
Prendo un punto $x \in U$. Poiché $U$ è aperto in $\mathcal{T}$, esiste una palla $B_d(x, \varepsilon) \subseteq U$.
Quindi, posso trovare una open ball $B_{d'}(x, \delta)$ tale che: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$
Dato che $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$, segue che $B_{d'}(x, \delta) \subseteq U$. Quindi, l'insieme $U$ è aperto anche nella topologia $\mathcal{T}'$.

Questo completa la dimostrazione in entrambe le direzioni.

E così via.