La distanza di Levenshtein

Questo tipo di calcolo è molto utile, ad esempio, nei correttori ortografici, dove si confrontano parole simili per suggerire correzioni. E' utilizzato per valutare la somiglianza tra stringhe.

In pratica, per calcolare la distanza di Levenshtein, costruisco una matrice in cui ogni cella rappresenta il costo minimo per trasformare una sottostringa in un’altra, passando di cella in cella per accumulare il numero minimo di operazioni.

Una particolarità è che, a differenza della distanza di Hamming, la distanza di Levenshtein funziona anche con stringhe di lunghezza diversa.

Un esempio pratico

Ad esempio, considero le stringhe $ s $ e $ t $

$$ s = "kitten" $$

$$ t = "sitting" $$

Voglio calcolare la distanza di Levenshtein tra queste due parole, cioè il numero minimo di modifiche (inserimenti, cancellazioni, o sostituzioni di caratteri) per trasformare "kitten" in "sitting".

1. Operazione di sostituzione
   Sostituisco la $ k $  con la $ s $ $$ "kitten" \rightarrow "sitten" $$
2. Operazione di sostituzione
   Sostituisco la $ e $ con la $ i $ $$ "sitten" \rightarrow "sittin"  $$
3. Operazione di inserimento
   Inserisco una $ g $ alla fine $$ "sittin" \rightarrow "sitting"  $$

In totale, ho effettuato 3 operazioni (2 sostituzioni e 1 inserimento), quindi la distanza di Levenshtein tra "kitten" e "sitting" è 3.

Per rappresentare questo risultato posso costruire una matrice di dimensione \( (m+1) \times (n+1) \), dove \( m \) è la lunghezza di "kitten" (6) e \( n \) è la lunghezza di "sitting" (7).

Includo una riga e una colonna in più per considerare le trasformazioni da e verso la stringa vuota.

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1
i	2
t	3
t	4
e	5
n	6

La cella \( (0, j) \) rappresenta il costo per trasformare una stringa vuota nella sottostringa di "sitting" fino a \( j \), quindi incremento il costo da 0 a 7.

La cella \( (i, 0) \) rappresenta il costo per trasformare la sottostringa di "kitten" fino a \( i \) in una stringa vuota, quindi incremento il costo da 0 a 6.

Ora, per ciascuna cella \( (i, j) \), calcolo il costo minimo considerando:

1. Cancellazione dalla stringa "kitten" (costo della cella sopra, \( +1 \))
2. Inserimento in "kitten" (costo della cella a sinistra, \( +1 \))
3. Sostituzione (costo della cella in diagonale) se i caratteri sono diversi (altrimenti nessun costo aggiuntivo).

Compilo passo passo la matrice:

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1	1	2	3	4	5	6	7
i	2	2	1	2	3	4	5	6
t	3	3	2	1	2	3	4	5
t	4	4	3	2	1	2	3	4
e	5	5	4	3	2	2	3	4
n	6	6	5	4	3	3	2	3

Ad esempio, per trasformare la stringa vuota in "s", "si", "sit", etc., il costo cresce di 1 per ogni colonna.

Per trasformare "k", "ki", "kit", etc., nella stringa vuota, il costo cresce di 1 per ogni riga.

• Nella cella (1,1) è indicato il costo per trasformare "k" in "s" ovvero 1 perché è necessaria una sola sostituzione (k→s).
  
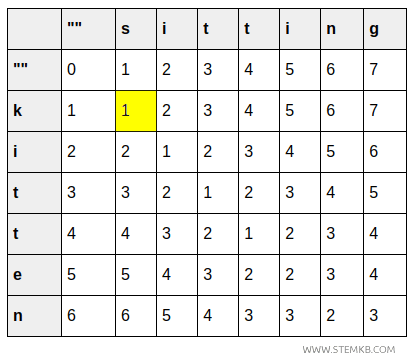
• Nella cella (2,2) è indicato il costo per trasformare "ki" in "si" ovvero sempre 1, perché la seconda lettera è uguale (i).
• Nella cella (3,3) è indicato il costo per trasformare "kit" in "sit" ovvero sempre 1, perché la terza lettera è uguale (t).
• Nella cella (4,4) è indicato il costo per trasformare "kitt" in "sitt" ovvero sempre 1, perché la quarta lettera è uguale (t).
• Nella cella (5,5) è indicato il costo per trasformare "kitte" in "sitti" che diventa 2, perché bisogna sostituire la lettera (e→i)
  
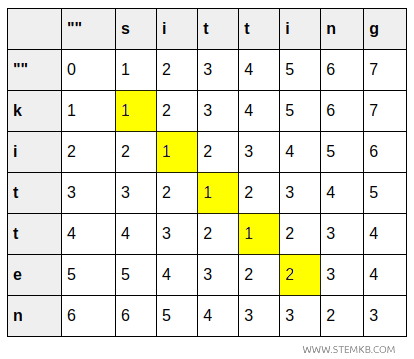
• Nella cella (6,6) è indicato il costo per trasformare "kitten" in "sittin" che resta 2, perché la sesta lettera è uguale (n).
• Nella cella (6,7) è indicato il costo per trasformare "kitten" in "sitting" che diventa 3, perché devo aggiungere la lettera (g).
  

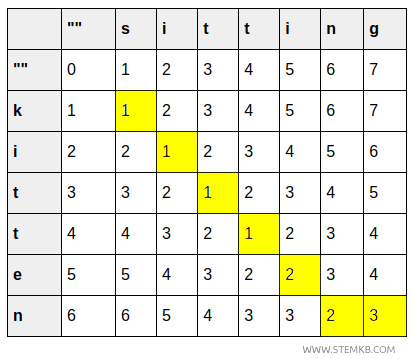
In questo modo, arrivo all’ultima cella che contiene il costo finale

L'elemento in basso a destra, \( (6,7) \), contiene il costo minimo per trasformare "kitten" in "sitting", che è 3.

Questo valore corrisponde alla distanza di Levenshtein, come ho visto anche nei calcoli precedenti: serve 1 sostituzione (`k → s`), 1 sostituzione (`e → i`) e 1 inserimento (`g`).

Topologia indotta dalla distanza di Levenshtein

La distanza di Levenshtein definisce uno spazio metrico sulle stringhe, proprio come fa la distanza di Hamming, perché soddisfa le proprietà fondamentali di una metrica.

1. Non negatività: La distanza di Levenshtein tra due stringhe \( x \) e \( y \) è sempre maggiore o uguale a zero, e \( D_L(x, y) = 0 \) solo se \( x = y \). Questo significa che non ci sono operazioni necessarie per trasformare una stringa in se stessa, quindi la distanza è zero solo per stringhe identiche.
2. Simmetria: La distanza di Levenshtein è simmetrica, cioè \( D_L(x, y) = D_L(y, x) \). Il numero di operazioni per trasformare \( x \) in \( y \) è lo stesso che per trasformare \( y \) in \( x \), dato che le operazioni (inserimento, cancellazione e sostituzione) si possono applicare in entrambi i sensi.
3. Disuguaglianza triangolare: La distanza di Levenshtein soddisfa la disuguaglianza triangolare, cioè \( D_L(x, z) \leq D_L(x, y) + D_L(y, z) \). In altre parole, la distanza diretta tra \( x \) e \( z \) non è mai maggiore della distanza ottenuta passando per una terza stringa \( y \). Questo accade perché ogni operazione necessaria per trasformare \( x \) in \( z \) può essere "composta" dalle operazioni necessarie per passare da \( x \) a \( y \) e poi da \( y \) a \( z \).

Grazie a queste proprietà, la distanza di Levenshtein genera uno spazio metrico sulle stringhe.

Essendo una distanza che soddisfa gli assiomi di uno spazio metrico, mi permette anche di definire una topologia metrica indotta sulle stringhe.

Dato un raggio \( r \) e una stringa \( x \), posso costruire una open ball centrata in \( x \) definita come l'insieme di tutte le stringhe \( y \) la cui distanza di Levenshtein da \( x \) è minore di \( r \):

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$

Le unioni delle open ball \( B(x, r) \) definiscono gli insiemi aperti della topologia.

Questa costruzione ha applicazioni importanti, soprattutto in ambiti dove è utile considerare la "vicinanza" tra stringhe, Ad esempio, nella correzione automatica delle parole, quando un termine ha una distanza di Levenshtein piccola rispetto a un'altra parola del dizionario.

Quindi, grazie alla distanza di Levenshtein, posso trattare le stringhe come elementi di uno spazio metrico e sfruttare la topologia metrica indotta per ragionare sulla loro vicinanza.

Un esempio pratico

Considero un insieme \( X \) di stringhe di lunghezza 3:

$$ X = \{\text{"cat"}, \text{"bat"}, \text{"cut"}\} $$

Definisco una base per la topologia, considerando le open ball di raggio \( r = 2 \) centrata su ciascuna stringa di \( X \).

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$ 

Ciascuna palla aperta con raggio \( r = 2 \) include tutte le stringhe che distano esattamente 1 dalla stringa centrale, secondo la distanza di Levenshtein.

Nota. Utilizzare un raggio \( r = 2 \) implica considerare stringhe che differiscono in al massimo una posizione da quella centrale, poiché la definizione di "insieme aperto" esclude il bordo. In altre parole, per un insieme aperto con raggio \( r = 2 \), la relazione è "strettamente minore di 2": $$ B(x, 2) = \{ y \mid D_L(x, y) < 2 \} $$ Per definire, invece, gli "insiemi chiusi" che includono anche il bordo, dovrei utilizzare una relazione "minore o uguale a 2", ossia includere tutte le stringhe a distanza al massimo di 2 operazioni dalla stringa centrale: $$ C(x, 2) = \{ y \mid D_L(x, y) \le 2 \} $$

Verifico quali sono le open ball aperte di raggio \( 2 \) per ciascuna stringa in \( X \):

1. Open ball aperta centrata in "cat"
   $$ B(\text{"cat"}, 2) = \{\text{"cat"}, \text{"bat"} \} $$
   Tutte queste stringhe richiedono al massimo una sola operazione di sostituzione di una lettera per trasformare la parola "cat", in "bat", "rat" o "mat".
2. Open ball aperta centrata in "bat"
   $$ B(\text{"bat"}, 2) = \{\text{"bat"}, \text{"cat"} \} $$
   Questa open ball include tutte le stringhe che possono essere trasformate in "bat" con al massimo una sola operazione
3. Open ball aperta centrata in "cut"
   $$ B(\text{"cut"}, 2) = \{\text{"cut"}\} $$
   In questo caso nessuna stringa dell'insieme $ X $ può essere trasformata in "cut" con al massimo una sola operazione. Solo la parola "cut" stessa appartiene a questo insieme perché è trasformabile in se stessa con zero operazioni.

Ora, gli insiemi \( B(\text{"cat"}, 2) \), \( B(\text{"bat"}, 2) \) e \( B(\text{"cut"}, 2) \) formano una base per la topologia indotta dalla distanza di Levenshtein con raggio \( r = 1 \).

Con questa base, posso ottenere tutti gli altri insiemi aperti come unioni arbitrarie delle open ball di raggio \( 2 \).

Ad esempio, l'unione di \( B(\text{"bat"}, 1) \) e \( B(\text{"cut"}, 1) \)

$$ B(\text{"bat"}, 1) \cup B(\text{"cut"}, 1) $$

Sapendo che $ B(\text{"cat"}, 2) = \{\text{"cat"}, \text{"bat"} \} $ e $ B(\text{"cut"}, 2) = \{\text{"cut"}\} $

$$ B(\text{"bat"}, 1) \cup B(\text{"cut"}, 1) =  \{\text{"cat"}, \text{"bat"} \} \cup \{\text{"cut"}\} $$

$$ B(\text{"bat"}, 1) \cup B(\text{"cut"}, 1) =  \{\text{"cat"}, \text{"bat"} , \text{"cut"}\} $$

L'insieme $ \{\text{"cat"}, \text{"bat"} , \text{"cut"}\} $ è un altro insieme aperto nella topologia.

Grazie a questa costruzione, ho una topologia metrica su \( X \) indotta dalla distanza di Levenshtein, e posso generare qualsiasi insieme aperto come unione di questi elementi di base.

E così via.