Equivalenza delle metriche

Due spazi metrici sono equivalenti se esiste una funzione $f : X \to Y$ che:

È biettiva: ogni elemento di $X$ corrisponde esattamente a uno e un solo elemento di $Y$, e viceversa.
Preserva le distanze: per tutti i punti $x_1, x_2 \in X$, la distanza tra $x_1$ e $x_2$ nello spazio $X$ è la stessa che tra i loro corrispondenti $f(x_1)$ e $f(x_2)$ nello spazio $Y$. Formalmente: $$ d_X(x_1, x_2) = d_Y(f(x_1), f(x_2)) $$

Se esiste questa funzione, gli spazi $X$ e $Y$ sono isometrici e si dice che sono equivalenti.

In altre parole, l’equivalenza per le metriche si basa sull’idea di confrontare due spazi metrici ($X, d_X$ e $Y, d_Y$) per capire se sono "essenzialmente uguali" rispetto alle distanze che definiscono.

Se due spazi metrici sono isometrici, allora hanno la stessa topologia, ovvero gli insiemi aperti (o la "forma generale" dello spazio) sono identici. Tuttavia, non vale il contrario.
Se due spazi condividono la stessa topologia non è detto che siano anche isometrici (equivalenti) perché l’isometria è un concetto più forte dell’equivalenza topologica, in quanto richiede che le distanze siano esattamente le stesse, non solo la struttura degli insiemi aperti.

Un esempio pratico

Considero due spazi metrici:

$X = \{a, b, c\}$ con la metrica $d_X$, definita così: $$ d_X(a, b) = 1, \quad d_X(b, c) = 2, \quad d_X(a, c) = 3 $$
$Y = \{p, q, r\}$ con la metrica $d_Y$, definita così: $$ d_Y(p, q) = 1, \quad d_Y(q, r) = 2, \quad d_Y(p, r) = 3 $$

Ora, definisco una funzione $f : X \to Y$ come:

$$ f(a) = p, \quad f(b) = q, \quad f(c) = r $$

Vediamo se preserva le distanze:

$d_X(a, b) = 1$ e $d_Y(f(a), f(b)) = d_Y(p, q) = 1$
$d_X(b, c) = 2$ e $d_Y(f(b), f(c)) = d_Y(q, r) = 2$
$d_X(a, c) = 3$ e $d_Y(f(a), f(c)) = d_Y(p, r) = 3$

Poiché tutte le distanze sono preservate, la funzione $f$ è un’isometria, e quindi gli spazi metrici $X$ e $Y$ sono "isometrici", ossia equivalenti.

Esempio 2

Sul piano la metrica del taxi ($d_T$) e la metrica standard ($d$) inducono la stessa topologia, cioè hanno la stessa nozione di insieme aperto.

Devo stabilire se questi due spazi metrici sono anche isometrici.

Nella metrica del taxi ($d_T$) la distanza tra due punti $(x_1, y_1)$ e $(x_2, y_2)$ è data da:

$$ d_T((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2| $$

Questa metrica misura la distanza come se ci si muovesse lungo una griglia, seguendo linee orizzontali e verticali (come un taxi in una città con strade a griglia).

Nella metrica standard ($d$) la distanza tra due punti $(x_1, y_1)$ e $(x_2, y_2)$ è data dalla formula euclidea:

$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$

Questa è la distanza "diretta" tra i due punti, come una linea retta.

Considero l'ipotesi per assurdo che esista un'isometria $f : \mathbb{R}^2 \to \mathbb{R}^2$ che preservi le distanze tra i punti sia nella metrica del taxi ($d_T$) sia in quella standard ($d$).

Per verificarla, prendo 2 punti del piano $ A = (1, 1) $ e $ B = (2, 2) $.

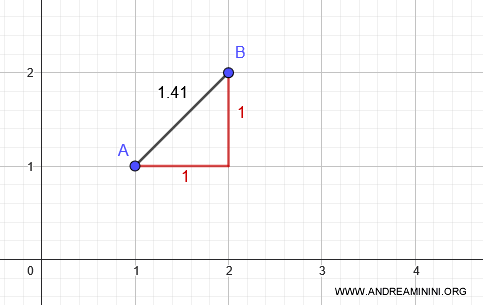
esempio

La distanza tra i due punti nella metrica del taxi è 2

$$ d_T((2, 2), (1, 1)) = |2 - 1| + |2 - 1| = 2 $$

Nella metrica standard la distanza tra i due punti è 1,41

$$ d((1, 1), (2, 2)) = \sqrt{(1 - 2)^2 + (1 - 2)^2} = \sqrt{2} \approx 1,41 $$

Nella metrica standard la distanza tra questi punti è diversa dalla metrica del taxi e questo porta a una contraddizione.

Poiché non è possibile costruire un'isometria che preservi le distanze tra i due spazi metrici, posso dedurre che il piano con la metrica del taxi non è isometrico al piano con la metrica standard.

In conclusione, il piano con la metrica del taxi ($d_T$) non è isometrico al piano con la metrica standard ($d$), anche se le due metriche inducono la stessa topologia, cioè hanno la stessa nozione di insieme aperto.

E così via.