Teorema della metrica limitata

In uno spazio metrico \( (X, d) \) si può costruire una nuova metrica limitata \( d'(x, y) = \min(d(x, y), 1) \) che induce la stessa topologia di \( d \), quindi gli insiemi aperti definiti da \( d \) e \( d' \) coincidono.

In altre parole, viene definita una nuova metrica \(d'(x, y)\) a partire dalla metrica \(d(x, y)\) in uno spazio metrico \((X, d)\), dove:

$$ d'(x, y) = \min(d(x, y), 1) $$

Le nuova metrica \(d'(x, y)\) prende il valore di \(d(x, y)\), a meno che non superi 1.  Questo rende la metrica \(d'\) limitata, perché non può mai superare 1.

La metrica \( d' \) induce la stessa topologia della metrica iniziale \( d \).

Questo significa che gli insiemi aperti definiti da \(d'\) sono gli stessi definiti da \(d\). Quindi, la "forma" degli insiemi aperti nello spazio non cambia, anche se la metrica \(d'\) è limitata.

Nota. In generale, potrei anche sostituire \(1\) con qualsiasi altro valore \(\varepsilon > 0\). $$ d'(x, y) = \min(d(x, y), \varepsilon) $$ In questo caso le distanze non supererebbero \(\varepsilon\) e le metriche indotte genererebbero la stessa topologia. Per semplicità, farò l'esempio con il limite fissato a $ \varepsilon = 1 $.

Un esempio pratico

Considero lo spazio \( \mathbb{R} \) con la metrica standard:

$$ d(x, y) = |x - y| $$

Poi definisco una nuova metrica limitata:

$$ d'(x, y) = \min(|x - y|, 1) $$

Nella nuova metrica le distanze non possono superare 1.

Ad esempio, se prendo due punti \( x = 2 \) e \( y = 5 \), con la metrica originale la distanza è \( d(2, 5) = |2 - 5| = 3 \), ma con la nuova metrica limitata la distanza è \( d'(2, 5) = \min(3, 1) = 1 \).  Se invece \( x = 2 \) e \( y = 2.5 \), allora \( d'(2, 2.5) = \min(|2 - 2.5|, 1) = 0.5 \), che coincide con la metrica originale perché \( |2 - 2.5| < 1 \). In quest'altro caso la distanza è la  stessa ovvero $ d = d' = 0.5 $. $$ \begin{array}{|c|c|c|c|} \hline x & y & d & d' \\  \hline  2 & 5 & 3 & 1 \\  \hline 2 & 2.5 & 0.5 & 0.5 \\  \hline 6 & 8 & 2 & 1 \\  \hline \end{array} $$

La nuova metrica \( d' \) "tronca" le distanze maggiori di 1, ma i concetti di vicinanza e insiemi aperti rimangono invariati, quindi la topologia indotta da \( d \) e \( d' \) è la stessa.

Perché la topologia rimane invariata?

Gli insiemi aperti della topologia sono definiti come unioni di open ball.

Anche se le open ball di \(d'\) possono essere più piccole di quelle di \(d\), posso sempre combinare più open ball di \(d'\) per coprire un insieme aperto di \(d\).

Ad esempio, considero una open ball $ B_d(3, 2) $ centrata in \(3\) con raggio \(2\).

Questa open ball è l'insieme di tutti i punti \(y \in \mathbb{R}\) tali che la distanza tra \(x\) e \(y\) è strettamente minore di \(r = 2 \), cioè:

$$ B_d(x, r) = \{y \in \mathbb{R} \mid d(x, y) < r\} $$

In questo caso $ x=3 $ e $ r = 2 $

$$ B_d(3, 2) = \{y \in \mathbb{R} \mid d(3, y) < 2\} $$

Nel caso della metrica standard (\(d(x, y) = |x - y|\)), la palla aperta \(B_d(3, 2)\) include tutti i numeri reali \(y\) che soddisfano:

$$ |3 - y| < 2 $$

La condizione \(|3 - y| < 2\) si può riscrivere come:

$$ -2 < 3 - y < 2 $$

$$ -2-3 < 3 - y -3 < 2-3 $$

$$ -5 <  - y < -1 $$

$$ -5 \cdot(-1) <  - y \cdot(-1) < -1 \cdot(-1) $$

$$ 1 < y < 5 $$

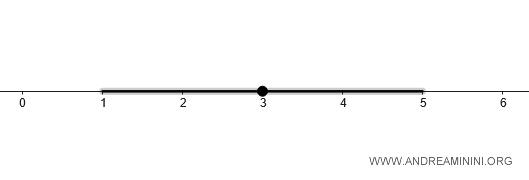
Quindi, \(B_d(3, 2)\) è l'intervallo aperto (1, 5) che contiene tutti i punti più vicini di \(2\) unità a \(3\) sulla retta reale.

$$ B_d(3, 2) = (1, 5) $$

Ecco la rappresentazione grafica sulla retta dei numeri reali.

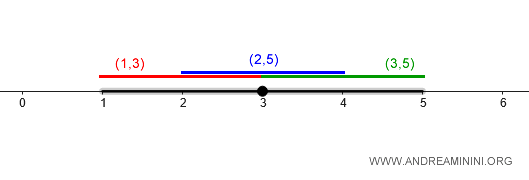
Per coprire l'intervallo \(  (1, 5)\) con \(d'\), posso usare unioni di palle più piccole, come:

$$ B_{d'}(2, 1) \cup B_{d'}(3, 1) = (4, 1) $$

La prima open ball copre l'intervallo (1,3), la seconda l'intervallo (2,4) e la terza l'intervallo (3,5) che coprono interamente l'interlvallo (1,5)

In questo modo, le metriche \(d'\) e \(d\) generano gli stessi insiemi aperti, quindi la topologia non cambia.

La dimostrazione

Devo dimostrare che \(d'\) induce la stessa topologia di \(d\).

Per prima dimostro che \(d'\) è una metrica, perché soddisfa tutte le proprietà di una metrica:

• \(d'(x, y) \geq 0\),
• \(d'(x, y) = 0\) solo se \(x = y\),
• \(d'(x, y) = d'(y, x)\),
• \(d'\) soddisfa la disuguaglianza triangolare.

A questo punto devo dimostrare che le topologie $ T $ e $ T' $ indotte rispettivamente da \(d\) e \(d'\) sono le stesse.

Procedo dimostrando che:

• La toipologia T è più fine di T'
• La topologia T' è più fine di T

A] Parte prima: T è più fine di T'

La topologia originale $ T $ indotta da $ d $ è più fine della topologia $ T' $ indotta dalla metrica limitata $ d' $ perché:

• Quando il raggio $ r $ della palla è minore o uguale a 1 le due open ball centrate nello stesso punto $ x $ usando le due metriche sono uguali. $$ B_d(x,r) = B_{d'}(x,r) $$
• Quando il raggio $ r $ della palla è maggiore di 1, la open ball della topologia originale è più grande di quella limitata. $$ B_d(x,r) \supseteq B_{d'}(x,r) $$

Dire che $ T $ è più fine di $ T' $ vuol dire che ogni insieme aperto in T' è contenuto anche in T. Quindi, ogni insieme aperto in T' è aperto anche in T.

B] Parte seconda: T' è più fine di T

D'altra parte, vale anche l'inverso, anche la topologia T' è più fine della topologia T.

• Quando il raggio $ r $ della palla è minore o uguale a 1 le due open ball centrate in $ x $ con le due metriche sono uguali. $$ B_d(x,r) = B_{d'}(x,r) $$
• Quando il raggio $ r $ della palla è maggiore di 1, la open ball della topologia originale è più grande di quella limitata. $$ B_d(x,r) \supseteq B_{d'}(x,r) $$ Tuttavia, sapendo che \(B_{d'}(x, 1)\) è una palla aperta nella topologia \(T'\) (indotta dalla metrica \(d'\)), posso costruire unioni di tante di queste palle per coprire qualsiasi insieme aperto di \(T\) (indotta dalla metrica \(d\)). Poiché l'unione di insiemi aperti è ancora un insieme aperto, deduco che anche la topologia T' è più fine di T.

Questo dimostra che ogni insieme aperto in \(T\) è anche aperto in \(T'\), completando il ragionamento.

C] Conclusione

In conclusione, ho dimostrato che T è più fine di T' e T' è più fine di T, quindi T=T' sono la stessa topologia.

E così via.