Poli e zeri complessi
Un polinomio di grado n a coefficienti reali ammette n zeri reali o complessi.
Le radici sono i valori dell'incognita che permettono l'annullamento (azzeramento) del polinomio.
$$ a_ns^n+a_{n-1}s^{n-1}+...a_1s^1+a_0 = 0 $$
che trasformato in forma fattorizzata diventa
$$ (s-p_1) \cdot (s-p_2) \cdot \cdot \cdot (s-p_n) $$
Il polinomio ammette n radici reali o complesse.
Se tra queste radici c'è una radice complessa, allora c'è anche la sua radice coniugata.
$$ \begin{cases} p_i = α + j ω \\ p_i=α - j ω \:\:\:\: \text{ (radice coniugata) } \end{cases} $$
La differenza tra poli e zeri. Nel caso di una funzione razionale, composta dal rapporto di due polinomi F(s) e X(s) $$ G(s)=\frac{F(s)}{X(s)} $$ si parla di zeri se le radici sono del polinomio al numeratore F(s), si parla di poli se le radici sono del polinomio al denominatore G(s).
Un esempio pratico
Devo trovare la radici di questo polinomio di 3° grado
$$ P(s)=s^3+2s^2+5s $$
Lo riscrivo in forma fattorizzata
$$ P(s)=s \cdot (s^2+2s+5) $$
Essendo un polinomio di terzo grado, il polinomio ha tre radici.
La prima radice è banale ed è un numero reale.
$$ s=0 $$
La seconda e la terza radice sono le soluzioni dell'equazione di 2° grado s2+2s+5
$$ \frac{-b ± \sqrt{b^2-4ac}}{2a} = \frac{-2 ± \sqrt{2^2-4(1)(5)}}{2(1)}= \frac{-2 ± \sqrt{-16}}{2} $$
Tuttavia, l'equazione s2+2s+5 non ha soluzioni reali perché non esiste la radice di un numero negativo nei numeri reali.
Per calcolare le soluzioni dell'equazione devo utilizzare i numeri complessi.
Nota. I numeri complessi sono nati appositamente per risolvere le radici quadrate dei numeri negativi. Secondo la regola, se n è un numero negativo n<0 allora la sua radice quadrata vale $$ i \cdot \sqrt{-n} $$ considerando che i2=-1 nei numeri complessi. Ad esempio, la soluzione della radice quadrata $$ \sqrt{-4} $$ nei numeri complessi è $$ i \cdot \sqrt{ -(-4)} = i \cdot \sqrt{4} = 2i $$
Le radici complesse dell'equazione di 2° grado s2+2s+5 sono:
$$ \frac{-2 ± \sqrt{-16}}{2} = \frac{-2 ± j \cdot \sqrt{-(-16)}}{2} = \frac{-2 ± j \cdot 4}{2} =-1 ± 2j $$
Per rappresentare la radice complessa (semplice e coniugata) del polinomio P(x) devo usare il piano di Gauss.
E' un piano in cui l'ascissa misura i numeri reali (Re) e l'ordinata i numeri immaginari (Im).
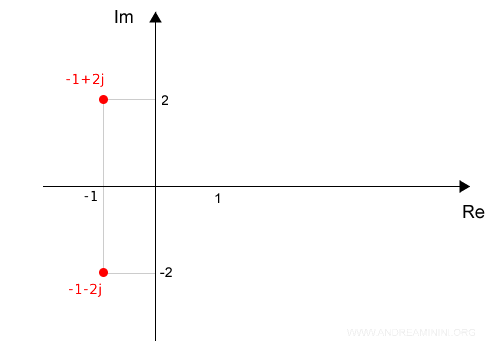
Quindi, il polinomio P(x) ha una radice reale p1 e una radice complessa p2
La radice complessa p2 ha una radice coniugata p'2
$$ p_1=0 \\ p_2 = a_2+jw =-1+j2 \\ p_2'=a_2-jw=-1-j2 $$
Ogni radice ha molteplicità v=1 perché non ci sono radici ripetute.
Pertanto, nel polinomio P(s) ci sono R=1 radici reali distinte e S=1 coppie di radici complesse e coniugate distinte.
Considerando anche le coniugate ci sono n=3 radici
$$ n = R + 2S = 1 + 2·1 =3 $$
Il piano di Gauss mi permette di rappresentare anche i numeri reali sulle ascisse, ponendo la parte immaginaria a zero.
Quindi posso usarlo per rappresentare tutte le radici del polinomio, sia reali che complesse.
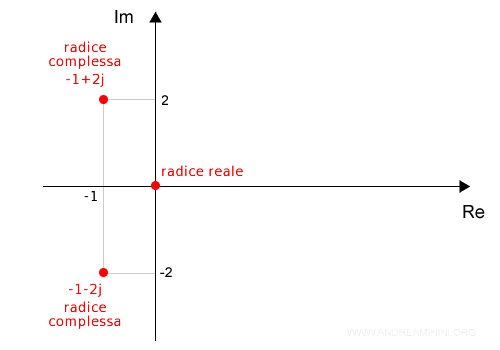
In conclusione, la forma fattorizzata diventa
$$ (s-p_1) \cdot (s-p_2) \cdot (s-p'_2) $$
$$ (s) \cdot (s-(-1+j2)) \cdot (s-(-1-j2)) $$
E così via.
