Resto di una serie

Il resto n-simo di una serie è una serie ottenuta eliminando i primi n termini della serie. $$ R_n = \sum_{k=n+1}^{\infty} a_k \:\:\:\:\:\: n \in N $$

Un esempio pratico

Prendo in considerazione una serie

$$ a_n = \sum_{k=1}^{\infty} \frac{1}{k(k+1)} $$

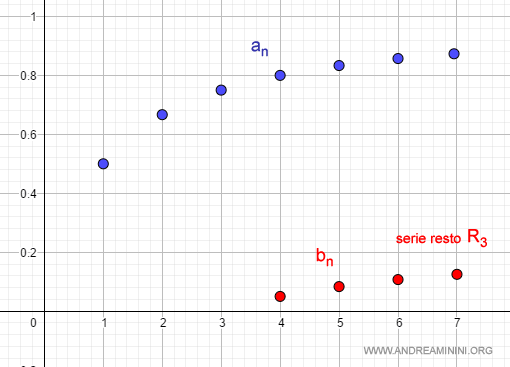
I primi termini della serie sono

$$ a_1 = \frac{1}{2} \\ a_2 = \frac{1}{2} + \frac{1}{6} \\ a_3 = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} \\ a_4 = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} \\ a_5 = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} \\ \vdots $$

Il resto R₃ della serie è la serie composta da n=4 in poi.

$$ R_n = \sum_{k=n+1}^{\infty} \frac{1}{k(k+1)} $$

$$ R_3 = \sum_{k=4}^{\infty} \frac{1}{k(k+1)} $$

I primi termini della serie resto sono:

$$ b_1=0 \\ b_2=0 \\ b_3=0 \\ b_4 = \frac{1}{20} \\ b_5 = \frac{1}{20} + \frac{1}{30} \\ b_6 = \frac{1}{20} + \frac{1}{30} + \frac{1}{42} \\ \vdots $$

Dal punto di vista grafico

Il teorema di convergenza della serie resto

Se una serie a_k è convergente, $$ \sum_{k=1}^{\infty} a_k $$ allora anche la sua serie resto n-simo R_n è convergente. $$ R_n = \sum_{k=n+1}^{\infty} a_k $$

Dimostrazione

Data una serie a_k convergente per ipotesi e la sua serie serie resto n-esimo R_n = Σb_k.

$$ \sum_{k=1}^{\infty} a_k $$

$$ \sum_{k=n+1}^{\infty} b_k $$

Per ogni m>n i termini delle serie sono sono uguali.

$$ a_m = b_m \:\:\: \forall m>n $$

Spiegazione. La serie resto R_n ha i primi n termini nulli. I successivi termini sono uguali alla serie. Pertanto, la serie bk (così ho chiamato la serie resto) è b_k=0 da 1 a n e b_k=a_k da m=n+1 in poi.

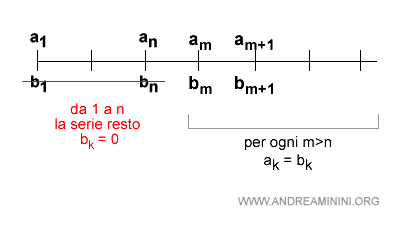
Pertanto, per ogni m>n la differenza dei termini delle serie (b_m-a_m) è nulla.

$$ b_m - a_m = 0 $$

Quindi, per ogni m>n la serie b_k-a_k da 1 a m è uguale alla serie b_k-a_k da 1 a n

$$ \sum_{k=1}^{m} (b_k -a_k) = \sum_{k=1}^{n} (b_k - a_k) $$

Detto in altri termini, la serie b_k-a_k è costante per ogni m>n. Non cambia più.

Spiegazione. I primi termini della serie resto b_k da 1 a n sono nulli (b_k=0). Quindi, da 1 a n la differenza b_k-a_k=-a_k. D'altra parte, ogni ulteriore termine da n+1 in poi è nulla b_k-a_k=0 perché a_k=b_k. Pertanto, da n+1 in poi la sommatoria parziale è sempre Σ b_n-a_n.

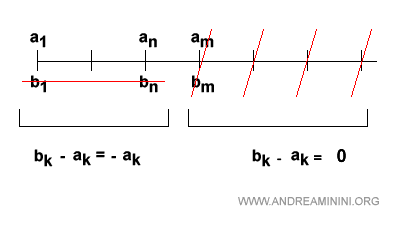
Quindi, per ogni m>n la serie differenza b_k-a_k è sempre uguale alla serie a_k da 1 a n.

$$ \lim_{m \rightarrow \infty} \sum_{k=1}^m (b_k-a_k) = \sum_{k=1}^n (b_k-a_k) $$

Ne consegue che la serie b_k-a_k è convergente.

A questo punto ho due serie convergenti

$$ \sum_{k=1}^{\infty} a_k \:\:\:\ \text{per l'ipotesi iniziale} $$

$$ \sum_{k=1}^{\infty} b_k - a_k $$

Per una proprietà delle serie regolari la somma di due serie convergenti è uguale alla serie della somma dei termini generali che è a sua volta una serie regolare e convergente.

$$ \sum_{k=1}^{\infty} a_k + \sum_{k=1}^{\infty} (b_k-a_k) $$

$$ \sum_{k=1}^{\infty} a_k + (b_k-a_k) $$

$$ \sum_{k=1}^{\infty} a_k + b_k -a_k $$

$$ \sum_{k=1}^{\infty} b_k $$

In questo modo dimostro che anche la serie resto R_n= Σb_k è una serie convergente.

Esempio

Riprendo le serie dell'esempio iniziale

$$ a_n = \sum_{k=1}^{\infty} \frac{1}{k(k+1)} $$

$$ R_3 = \sum_{k=4}^{\infty} \frac{1}{k(k+1)} $$

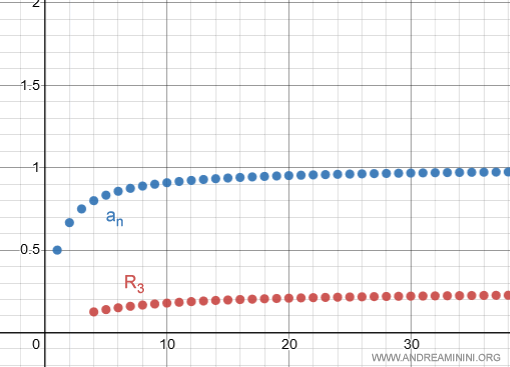
Entrambe le serie sono convergenti per n→∞

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k(k+1)} = 1$$

$$ \lim_{n \rightarrow \infty} \sum_{k=4}^{n} \frac{1}{k(k+1)} = 0.25 $$

Ecco la rappresentazione grafica delle due serie

Corollario

Se una serie a_k è convergente, il limite della serie resto R_n per _n→∞ è uguale a zero. $$ \lim_{n \rightarrow \infty } R_n = \lim_{n \rightarrow \infty } \sum_{k=n+1}^{\infty} a_k = 0 $$

Dimostrazione

Data una serie a_k convergente e la sua serie resto n-esimo R_n = b_k.

$$ \sum_{k=1}^{\infty} a_k $$

$$ R_n = \sum_{k=n+1}^{\infty} b_k $$

Per ogni m>n la differenza a_k-b_k=0 è nulla e la serie Σ(a_k-b_k) resta costante e pari alla sommatoria parziale Σ(a_n-b_n)

$$ \sum_{k=1}^m (a_k - b_k) = \sum_{k=1}^n (a_k - b_k) = \sum_{k=1}^n a_k $$

Spiegazione. Da 1 a n la serie resto b_k=0. Pertanto, da 1 a n la differenza a_k-b_k=a_k. Per ogni m>n i termini a_k=b_k sono uguali. Quindi, la loro differenza è nulla a_k-b_k=0. Dopo n la sere a_k-b_k resta costante e pari alla somma parziale a_n.

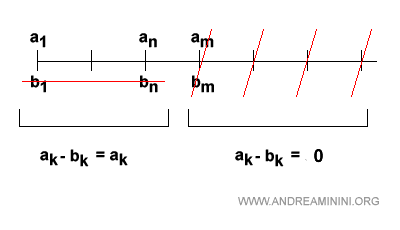
Quindi, per ogni m>n vale la seguente relazione di uguaglianza

$$ \sum_{k=1}^m (a_k - b_k) = \sum_{k=1}^n a_k $$

Calcolo il limite per m→∞ della relazione precedente

$$ \lim_{m \rightarrow \infty} \sum_{k=1}^m (a_k - b_k) = \lim_{m \rightarrow \infty} \sum_{k=1}^n a_k $$

$$ \sum_{k=1}^{\infty} (a_k - b_k) = \sum_{k=1}^n a_k $$

$$ \sum_{k=1}^{\infty} a_k - \sum_{k=1}^{\infty} b_k = \sum_{k=1}^n a_k $$

Sapendo che Σb_k=R_n

$$ ( \sum_{k=1}^{\infty} a_k ) - R_n = \sum_{k=1}^n a_k $$

Calcolo il limite per n→∞ della precedente relazione

$$ \lim_{n \rightarrow \infty} [ ( \sum_{k=1}^{\infty} a_k ) - R_n ] = \lim_{n \rightarrow \infty} \sum_{k=1}^n a_k $$

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{\infty} a_k - \lim_{n \rightarrow \infty} R_n = \lim_{n \rightarrow \infty} \sum_{k=1}^n a_k $$

$$ \sum_{k=1}^{\infty} a_k - \lim_{n \rightarrow \infty} R_n = \sum_{k=1}^{\infty} a_k $$

$$ \lim_{n \rightarrow \infty} R_n = \sum_{k=1}^{\infty} a_k - \sum_{k=1}^{\infty} a_k $$

$$ \lim_{n \rightarrow \infty} R_n = 0 $$

Ho dimostrato che la serie resto R_n converge a zero.

Esempio

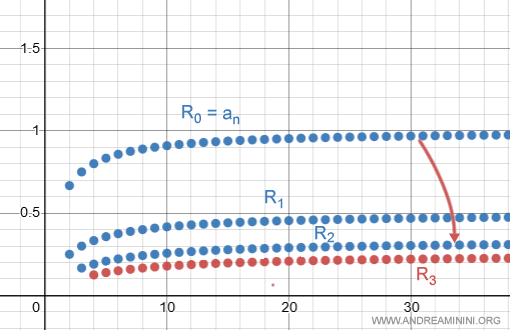
Riprendo l'esempio iniziale, la serie a_n è uguale alla serie resto R₀ e converge a 1

$$ \lim_{n \rightarrow \infty} R_0 = \lim_{n \rightarrow \infty} \sum_{k=1}^{\infty} \frac{1}{k(k+1)} = 1 $$

La serie resto R₁ converge a 0.5

$$ \lim_{n \rightarrow \infty} R_1 = \lim_{n \rightarrow \infty} \sum_{k=2}^{\infty} \frac{1}{k(k+1)} = 0.5 $$

La serie resto R₂ converge a 0.33

$$ \lim_{n \rightarrow \infty} R_2 = \lim_{n \rightarrow \infty} \sum_{k=3}^{\infty} \frac{1}{k(k+1)} = 0.33 $$

La serie resto R₃ converge a 0.25

$$ \lim_{n \rightarrow \infty} R_3 = \lim_{n \rightarrow \infty} \sum_{k=4}^{\infty} \frac{1}{k(k+1)} = 0.25 $$

Come si può notare, eliminando progressivamente i primi p=0,1,2,3 termini la serie resto R_n converge a un numero finito l che si avvicina sempre più a zero (1, 0.5, 0.33, 0.25).

Pertanto, per p→∞ la serie R_p converge a zero.

$$ \lim_{p \rightarrow \infty} R_p = \lim_{n \rightarrow \infty} \sum_{k=p+1}^{\infty} \frac{1}{k(k+1)} = 0 $$

Ecco la rappresentazione grafica delle prime tre serie di resto n-esime.

E così via.