Le operazioni con le serie
Le principali operazioni tra le serie regolari sono la somma e il prodotto per una costante o scalare.
Somma di due serie
Se le serie di termine generale ak e bk sono serie regolari e se $$ \sum_{k=1}^{\infty} a_k + \sum_{k=1}^{\infty} b_k $$ ha un significato nell'insieme dei numeri reali R, allora anche la serie di termine generale ak+bk è una serie regolare ed è $$ \sum_{k=1}^{\infty} (a_k+b_k) = \sum_{k=1}^{\infty} a_k + \sum_{k=1}^{\infty} b_k $$
Un esempio pratico
Prendo in considerazione due serie
$$ a_n = \sum_{k=1}^{n} \frac{2}{2^k} $$
$$ b_n = \sum_{k=1}^{n} \frac{3}{3^k} $$
Sono due serie regolari perché convergenti
$$ \lim_{ n \rightarrow \infty } \sum_{k=1}^{n} \frac{2}{2^k} = 2 $$
$$ \lim_{ n \rightarrow \infty } \sum_{k=1}^{n} \frac{3}{3^k} = 3 $$
Nota. Una serie è detta regolare se è convergente oppure divergente, ossia se esiste il limite della serie per n che tende a infinito ed è un limite finito o infinito.
Ecco la rappresentazione grafica delle due serie sul diagramma cartesiano
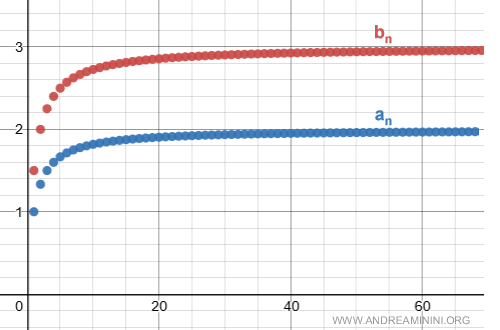
La loro somma ha un significato nell'insieme dei numeri reali
Nota. La somma deve avere un significato nell'insieme dei numeri reali. Ad esempio, la somma di due numeri finiti (l1+l2) ha sempre significato. La somma di un numero finito con infinito ha significato (l1+∞). Non ha invece significato la somma tra più infinito e meno infinito (∞-∞).
Pertanto, anche la serie composta dalla loro somma è una serie regolare
$$ (a_n + b_n) = \sum_{k=1}^{n} [ \frac{2}{2^k} + \frac{3}{2^k} ] $$
$$ (a_n + b_n) = \sum_{k=1}^{n} [ \frac{5}{2^k} ] $$
ed è una serie a sua volta convergente che converge a 5
$$ \lim_{ n \rightarrow \infty } (a_n + b_n) $$
$$ \lim_{ n \rightarrow \infty } \sum_{k=1}^{n} \frac{5}{2^k} = 5 $$
Dal punto di vista grafico
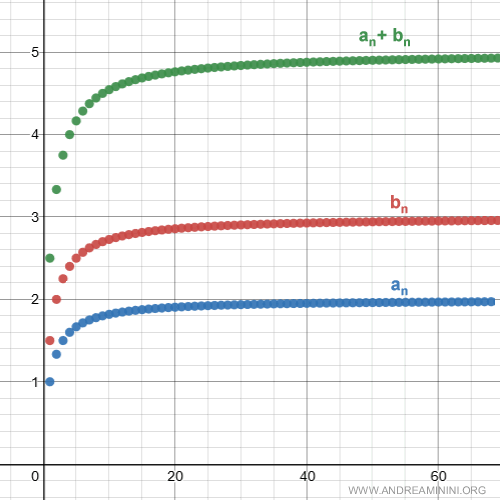
Prodotto tra una serie e uno scalare
Dato una costante c di R, se la serie di termine generale ak è una serie regolare, allora anche la serie di termine generale c·ak è una serie regolare ed è $$ \sum_{k=1}^{\infty} c \cdot a_k = c \cdot \sum_{k=1}^{\infty} a_k $$
Un esempio pratico
Prendo in considerazione la serie
$$ s_n = \sum_{k=1}^{n} \frac{1}{2^k} $$
E' una serie convergente perché per n→∞ converge a 1.
$$ \lim_{ n \rightarrow \infty } \sum_{k=1}^{n} \frac{1}{2^k} = 1 $$
Ecco il grafico della serie.
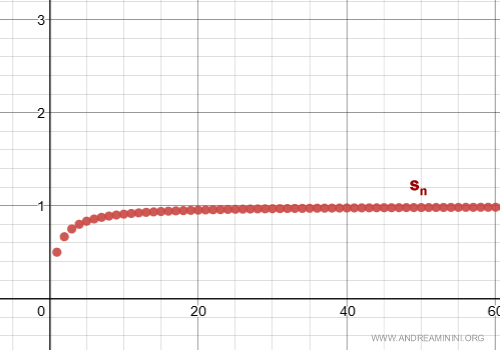
Ora moltiplico la serie c=2
$$ s_n = \sum_{k=1}^{n} \: 2 \cdot \frac{1}{2^k} $$
Essendo una serie regolare, perché convergente, posso applicare la regola del prodotto per uno scalare.
$$ s_n = 2 \cdot \sum_{k=1}^{n} \frac{1}{2^k} $$
Anche la serie 2·sn è regolare e convergente.
$$ \lim_{ n \rightarrow \infty } 2 \cdot \sum_{k=1}^{n} \frac{1}{2^k} = 2 $$
La serie converge 2·sn a 2.
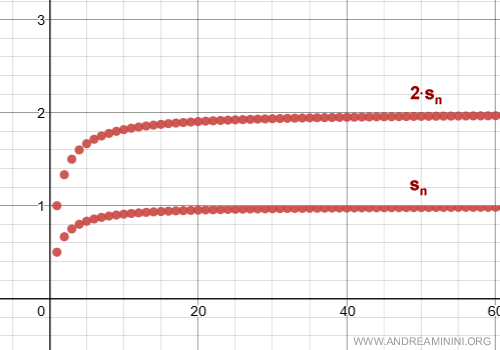
E così via.
