Criterio dell'integrale per lo studio della serie
Il criterio dell'integrale permette di studiare il carattere di una serie a termini positivi o definitivamente positivi quando il termine generale è una successione decrescente e infinitesima.
Come funziona
Per prima cosa verifico se la serie è a termini positivi o definitivamente positivi.
$$ \sum_{k=0}^{\infty} a_k $$
Nota. Una serie è a termine definitivamente positivi se a partire dall'indice k0 i termini sono tutti positivi. Quindi, nel caso della serie definitivamente positivi i primi termini potrebbero essere nulli o negativi.
Poi verifico se il termine generale della serie è una successione {ak} decrescente e infinitesima.
$$ \lim_{k \rightarrow \infty} a_k = 0 $$
Se queste due condizioni sono soddisfatte posso usare il criterio dell'integrale.
Trasformo la successione {ak} in una funzione associata f(x).
$$ \{ a_k \} \rightarrow f(x) $$
Calcolo l'integrale della funzione associata tra gli estremi k0 e k.
Trasformo l'integrale in una successione ausiliaria {tk}.
$$ \{ t_k \} = \int_{k0}^k f(x) \ dx $$
Nota. Dove k0 è il primo valore intero usato nell'indice della serie. Ad esempio, se la serie inizia da k=0 allora k0=0, se inizia da k=1 allora k0=1, e via dicendo.
Il carattere della successione ausiliaria {tk} e la serie iniziale hanno lo stesso carattere.
- Se la successione ausiliaria {tk} diverge, anche la serie diverge.
- Se la successione ausiliaria {tk} converge, anche la serie converge.
Nota. Essendo una serie a termini positivi, è una serie regolare. Quindi può divergere o convergere.
Un esempio
Devo studiare il carattere di questa serie
$$ \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}} $$
E' una serie a termini positivi.
Nota. Essendo una serie a termini positivi è una serie regolare, può divergere o convergere. Purtroppo, la serie soddisfa anche la condizione necessaria di convergenza. $$ \lim_{k \rightarrow \infty} \frac{1}{\sqrt{k}} = 0 $$ Quindi, non posso dire ancora nulla sul carattere.
La successione {ak} è decrescente
$$ \{ \frac{1}{\sqrt{k}} \} \downarrow $$
La successione è anche infinitesima
$$ \lim_{k \rightarrow \infty} \frac{1}{\sqrt{k}} = 0 $$
Entrambe le condizioni del criterio dell'integrale sono soddisfatte.
Individuo la funzione associata alla successione {ak}
$$ \{ \frac{1}{\sqrt{k}} \} \rightarrow f(x) = \frac{1}{\sqrt{x}} $$
Poi calcolo l'integrale tra k0=1 e k della funzione associata per trovare la successione ausiliaria {tk}
$$ \{ t_k \} = \int_1^k \frac{1}{\sqrt{x}} \ dx $$
Per calcolare l'integrale trasformo la funzione integranda in una forma equivalente.
$$ \{ t_k \} = \int_1^k x^{-\frac{1}{2}} \ dx $$
In questo modo posso calcolare l'integrale di una potenza.
$$ \{ t_k \} = \int_1^k x^{-\frac{1}{2}} \ dx = [ \frac{x^{1-\frac{1}{2}}}{1-\frac{1}{2}} ]^k_1 $$
$$ \{ t_k \} = \frac{k^{1-\frac{1}{2}}}{1-\frac{1}{2}} - \frac{1^{1-\frac{1}{2}}}{1-\frac{1}{2}} $$
$$ \{ t_k \} = \frac{k^{1-\frac{1}{2}} -1^{1-\frac{1}{2}} }{1-\frac{1}{2}} $$
$$ \{ t_k \} = \frac{k^{\frac{2-1}{2}} -1^{\frac{2-1}{2}} }{\frac{2-1}{2}} $$
$$ \{ t_k \} = \frac{k^{\frac{1}{2}} -1^{\frac{1}{2}} }{\frac{1}{2}} $$
$$ \{ t_k \} = \frac{\sqrt{k} - \sqrt{1}} {\frac{1}{2}} $$
$$ \{ t_k \} = 2 \cdot ( \sqrt{k} - 1 ) $$
Ho trovato la successione ausiliaria {tk}.
A questo punto devo solo studiare il suo carattere per k→∞.
La successione ausiliaria diverge
$$ \lim_{k \rightarrow \infty} 2 \cdot ( \sqrt{k} - 1 ) = +\infty $$
Quindi, per il criterio dell'integrale anche la serie iniziale diverge perché hanno in comune lo stesso carattere.
$$ \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}} = +\infty $$
Dal punto di vista grafico ecco l'andamento divergente della serie
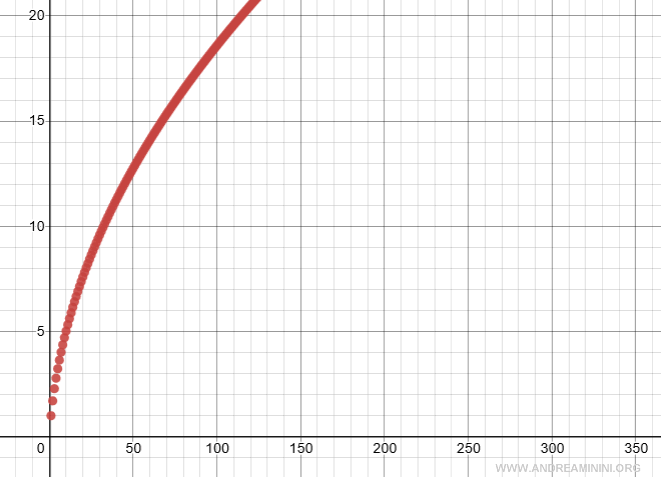
Nota. A conferma del risultato la serie che ho studiato è una serie armonica generalizzata con esponente compreso tra 0 e 1. Quindi, è divergente.
E così via.
