Le strutture algebriche
Cos'è una struttura algebrica
Una struttura algebrica è un insieme S con una o più operazioni definite in S. $$ (S,*) $$
Se ha una sola operazione è detta gruppoide.
Se l'operazione del gruppoide è associativa è detta semigruppo.
Se il semigruppo ha un elemento neutro si parla di monoide.
Cos'è un'operazione?
Un'operazione è un'applicazione (funzione) che relaziona gli elementi dell'insieme S con altri elmenti di S.
$$ *: S \rightarrow S $$
E' detta operazione binaria se relaziona le coppie di elementi di S con gli altri elementi dell'insieme stesso.
$$ *: S×S \rightarrow S $$
Un esempio di struttura algebrica
Esempio 1
Prendo come riferimento l'insieme dei numeri interi Z.
Poi considero l'addizione + come operazione.
$$ ( Z , + ) $$
Ho così ottenuto una struttura algebrica.
Ogni coppia di elementi di Z ( addendi ) è legata a un altro elemento di Z ( somma ).
$$ +: ZxZ \rightarrow Z $$
Nota. Se l'immagine dell'operazione non appartenesse all'insieme di origine (Z) non si potrebbe parlare di struttura algebrica.
Esempio 2
Prendo come riferimento l'insieme dei numeri da 1 a 10 e l'operazione di moltiplicazione (*).
$$ S = ( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ) $$
In questo caso (S,*) non è una struttura algebrica perché alcuni risultati non appartengono all'insieme S.
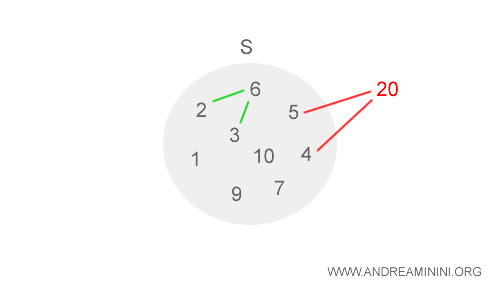
Ad esempio, il prodotto 4*5 è uguale a 20 e il numero 20 non è un elemento dell'insieme S.
$$ (1*2)=2 \\ (2*3)=6 \\ (4*5)=20 $$
Questa non è una struttura algebrica.
Uno stesso insieme S potrebbe essere una struttura algebrica rispetto a un'operazione e non esserlo rispetto a un'altra. Ad esempio, l'insieme dei numeri naturali N è una struttura algebrica (N,+) nei confronti dell'addizione ma non una struttura algebrica rispetto alla sottrazione (N,-) perché la differenza tra due numeri naturali non è detto che sia un altro numero naturale, potrebbe essere un numero negativo.
La tavola di verità
Quando costruisco una struttura algebrica con un insieme finito di elementi, posso rappresentarla con la tavola di verità.
Esempio
Ho un insieme S composto da tre elementi {a,b,c} e un'operazione |
$$ (S,|) $$
L'operazione lega ogni coppia di elementi SxS a un altro elemento dell'insieme S.
Ecco la tavola di verità.
| a | b | c | |
|---|---|---|---|
| a | a | a | b |
| b | c | b | a |
| c | a | b | c |
E' una semplice struttura algebrica con una sola operazione, ossia un gruppoide.
E così via.
Attenzione. Nella tabella non ho usato una logica particolare per associare una coppia di elementi a un risultato. Ad esempio, non c'è una logica perché (a,b)=c. Poteva anche essere (a,b)=a oppure (a,b)=b. Il risultato dipende dalla funzione che scelgo o dal circuito logico. Ciò che conta per essere una struttura algebrica è che anche il risultato appartenga all'insieme S.
