Gruppo simmetrico
Cos'è un gruppo simmetrico?
Un gruppo simmetrico è un gruppo composto dalle permutazioni dei suoi elementi.
Spiegazione ed esempio
Ho un gruppo (X,*) e l'insieme X è composto da n elementi.
Ad esempio n=5.
$$ X = \{ 1,2,3,4,5 \} $$
Indico con S(X) l'insieme delle corrispondenze biunivoche tra l'insieme X e se stesso.
A volte è indicato anche come Sn.
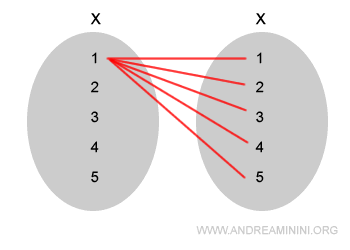
L'insieme S(X) può essere composto da n! permutazioni possibili, ossia 5!=120 permutazioni.
$$ S(X) = \{ 5,4,3,2,1 \} \\ S(X) = \{ 4,5,2,1,3 \} \\ S(X) = \{ 4,5,2,1,3 \} \\ \vdots $$
In pratica, l'insieme S(X) ha una cardinalità, ossia un numero di elementi, pari a n!
$$ |S(X)| = n! $$
$$ |S(X)| = 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$
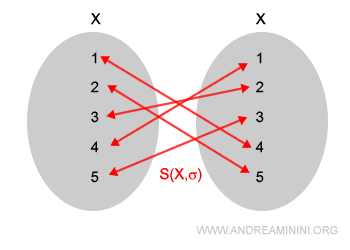
La composizione σ è una funzione che determina una corrispondenza biunivoca tra l'insieme iniziale X e una particolare permutazione.
$$ σ : X \rightarrow X $$ $$ σ : \{ 1,2,3,4,5 \} \rightarrow \{ 4,5,2,1,3 \} $$
Tutte le altre permutazioni sono escluse.
A tutti gli effetti la funzione di composizione è un gruppo simmetrico.
$$ (S(X),σ ) $$
E' detto gruppo simmetrico di grado n.
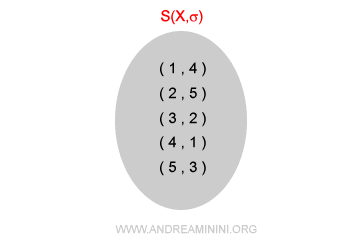
In questo caso, è un gruppo simmetrico di grado 5.
$$ \sigma:X \rightarrow X $$ $$ 1 \rightarrow 4 \\ 2 \rightarrow 5 \\ 3 \rightarrow 2 \\ 4 \rightarrow 1 \\ 5 \rightarrow 3 $$
Posso rappresentare la corrispondenza biunivoca σ anche in forma tabellare o matriciale.
$$ σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 5 & 2 & 1 & 3 \end{pmatrix} $$
Dove nella prima riga ho posto l'insieme di elementi X e nella seconda riga la corrispondenza biunivoca sigma ( S(X), sigma ).
Inversa della permutazione
La permutazione inversa di un gruppo simmetrico si ottiene invertendo l'applicazione che determina la corrispondenza biunivoca.
Esempio
Se la corrispondenza biunivoca iniziale è
$$ σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 5 & 2 & 1 & 3 \end{pmatrix} $$
alla la permutazione inversa è
$$ σ^{-1} = \begin{pmatrix} 4 & 5 & 2 & 1 & 3 \\ 1 & 2 & 3 & 4 & 5 \end{pmatrix} $$
e riordinando i ordine crescente gli elementi della prima riga
$$ σ^{-1} = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 3 & 5 & 1 & 2 \end{pmatrix} $$
L'elemento neutro
L'elemento neutro è la corrispondenza biunivoca con una permutazione S(X) uguale a quella iniziale.
E' indicato con la notazione id.
Esempio
$$ id = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 2 & 3 & 4 & 5 \end{pmatrix} $$
La potenza e il periodo della permutazione
Una permutazione può essere elevata alla potenza k, dove k è un esponente intero positivo.
La potenza è un composto ripetuto k volte.
Esempio
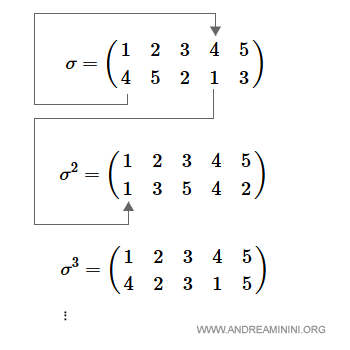
Nota. Se la potenza k determina l'elemento neutro (id) della permutazione, allora la permutazione ha ordine/periodo k.

La permutazione ha periodo 6.
Le orbite
Le orbite sono le classi di equivalenza di un elemento x rispetto alla potenza i-esima della composizione σi. L'insieme delle classi di equivalenza formano un'orbita. $$ O_σ = \{ σ^0(x), σ^1(x), ... , σ^{m-1}(x) \} $$
Dove σ è l'elemento x stesso.
Esempio
La classe di equivalenza m=2 dell'elemento x=3 rispetto alla composizione σm è 5.
E' detta orbita Oσ(3)=(3,2).

L'intero positivo minimo m=m(x) è il numero intero che rende σm uguale a 5.
Nel caso di x=3 l'intero positivo minimo m(3) è uguale a 3 perché σ(3) = 3 e Oσ(3)=(3,2,5).

L'insieme ordinato delle orbite Oσ(x) con m(x)=x è detto ciclo di lunghezza m.
Nel caso di Oσ(3)=3, il ciclo è (3,2,5) di lunghezza m=3.
Qual è la differenza tra orbita e ciclo? Un'orbita è semplicemente un sottoinsieme di X e l'ordine di importanza non ha importanza. Ad esempio l'orbita O(3,2,5) è uguale a O(2,3,5), O(2,5,3), O(5,3,2), O(3,5,2), O(5,2,3). Viceversa, in un ciclo l'ordine degli elementi ha importanza. Ad esempio, il ciclo (3,2,5) è uguale a (5,3,2) e perché gli elementi scorrono in sequenza ma non è uguale (3,5,2) perché l'ordine degli elementi è diverso.

I cicli delle permutazioni
Analizzando le orbite emergono dei cicli.
Un ciclo è una permutazione che torna all'elemento di partenza.
Esempio
In questa permutazione emergono due cicli disgiunti:

Cosa sono due cicli disgiunti? Due cicli sono disgiunti se non hanno nessun elemento in comune.
Il primo ciclo è lungo 2 mentre il secondo 3.
$$ c_1 = \begin{pmatrix} 1 & 4 \\ 4 & 1 \end{pmatrix} $$ $$ c_2 = \begin{pmatrix} 2 & 3 & 5 \\ 5 & 2 & 3 \end{pmatrix} $$
Nota. Escludo il ciclo (4,1) perché è sempre il ciclo (1,4). Per lo stesso motivo escludo i cicli (3,2,5) e (5,3,2) perché sono sempre il ciclo (2,5,3).
Posso riscrivere i due cicli in questa forma equivalente:
$$ c_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 3 & 1 & 5 \end{pmatrix} $$ $$ c_2 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 5 & 2 & 4 & 3 \end{pmatrix} $$
Dove le posizioni mancanti sono riempite con gli stessi elementi.
Il prodotto dei due cicli disgiunti determina la permutazione originaria.
$$ c_1 \cdot c_2 $$ $$ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 3 & 1 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 5 & 2 & 4 & 3 \end{pmatrix} = $$ $$ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 5 & 2 & 1 & 3 \end{pmatrix} $$
C'è anche un'altra importante proprietà.
Il minimo comune multiplo dei cicli è uguale al periodo della permutazione originaria.
Esempio
$$ m(c_1) = 2 $$ $$ m(c_2) = 3 $$ $$ m = mcm(c_1,c_2) = 6 $$
In questo modo posso calcolare il periodo o ordine del ciclo osservando i cicli, senza dover analizzare tutti i passaggi delle permutazioni.
Le permutazioni di classe pari e dispari
- Ogni permutazione è il prodotto di trasposizioni (a,b).
- Se il numero delle trasposizioni è pari, la permutazione è detta pari
- Se il numero delle trasposizioni è dispari, la permutazione è detta dispari
$$ (1,2,3...,m) = (1, m) \cdot (1,m-1) \cdot ... \cdot (1,3) \cdot (1,2) $$
Esempio
La seguente permutazione è composta da m=3 elementi.
$$ ( 1, 2, 3 ) $$
Nota. Equivale alla notazione $$ \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
E' un 3-ciclo ( triciclo ).
Posso riscriverlo come prodotto di 2-cicli ( trasposizioni ) nel seguente modo
$$ ( 1, 3) \cdot (1,2) $$
E' una permutazione di classe pari perché è composta da due trasposizioni.
Equivale a
$$ \begin{pmatrix} 1 & 3 \\ 3 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$
Spiegazione
Leggendo da destra verso sinistra (importante)
- 1 va in 2 nel secondo 2-ciclo. 2 non è indicato nel primo 2-ciclo. Quindi, nella composizione 1 va in 2.
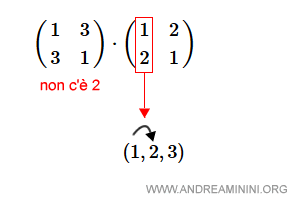
- 2 va in 1 nel secondo 2-ciclo. 2 va in 3 nel primo 2-ciclo. Quindi, nella composizione 2 va in 3.
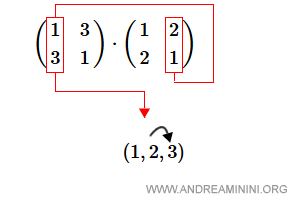
- 3 non è idicato nel secondo 2-ciclo. 3 va in 1 nel primo 2-ciclo. Quindi, nella composizione 3 va in 1.
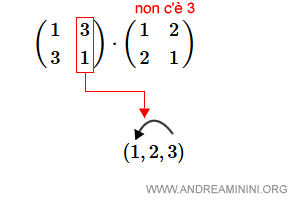
In conclusione la composizione di trasposizioni (1,3)·(1,2) equivale al ciclo (1,2,3) ossia.
$$ \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
Nota. Non è possibile scrivere una permutazione con un numeri pari e dispari di trasposizioni. Quindi, una permutazione è pari o dispari. Tutti i 3-cicli sono pari. Tutti i 4-cicli sono dispari. E così via.
Il numero n delle trasposizioni determina anche il segno della permutazione.
$$ sign(σ) = (-1)^n $$
Pertanto, le permutazioni pari hanno segno +1 mentre quelle dispari hanno segno -1.
Il sottogruppo alterno
Dato un sottogruppo Sn di un gruppo simmetrico, il sottogruppo alterno è l'insieme delle permutazioni pari ossia le permutazioni coni segno +1. E' indicato con An.
Esempio
Nel sottogruppo S3 le permutazioni possibili di un 3-ciclo sono sei (pari).
$$ \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$
Tra queste ci sono 3 permutazioni pari e 3 permutazioni dispari
$$ \frac{n!}{2} = \frac{3 \cdot 2 \cdot 1}{2} = \frac{6}{2} = 3 $$
Vediamo quali sono

Nota. Le permutazioni singole non sono cicli e non si scrivono per questa ragione la seconda permutazione non si scrive (1)(2,3) ma soltanto (2,3). Lo stesso discorso vale per la terza e la sesta permutazione.
Il gruppo alterno è composto dalle permutazioni
$$ A_3 = \{ id, (1,2,3) , (1,3,2) \} $$
La tavola di moltiplicazione
Una volta conosciuti i sottogruppi di S3 posso anche calcolare la tavola di moltiplicazione del gruppo S3.
Prima di farlo devo riscrivere le permutazioni nella notazione ciclica.

Poi le dispongo in tabella e calcolo la composizione delle permutazioni prese a due a due.
Il risultato è la tavola di moltiplicazione delle permutazioni del gruppo S3.

Le partizioni
E' opportuno notare che tutti i sottogruppi di S3 appartengono a tre classi di permutazioni.
- Un 1-ciclo ossia la permutazione identica (id).
Nota. La permutazione id è composta da tre cicli di lunghezza 1. Tuttavia, un ciclo di lunghezza 1 non si scrive. Per questa ragione si indica con il simbolo id.
- Tre 2-cicli ossia le permutazioni (1,2),(1,3) e (2,3) di lunghezza 2.
Nota. La permutazione (1,2) equivale alla composizione (1,2)(3). Poiché i cicli di lunghezza 1 non si scrivono, si indica soltanto il 2-ciclo ossia la trasposizione (1,2). Lo stesso vale per (1,3) e (2,3).
- Due 3-cicli ossia le permutazioni (1,2,3) e (1,3,2) di lunghezza 3.
Sono anche dette partizioni.
C'è un legame stretto tra ogni gruppo Sn di permutazioni e le partizioni del numero intero n.
Esempio
Il numero intero 3 ha le seguenti partizioni
- 3
- 2+1
- 1+1+1
Coincidono con le partizioni del gruppo di permutazioni S3.
- 3-ciclo = ad esempio (1,2,3) e (1,3,2)
- 2-ciclo = ad esempio (1,2) , (1,3) e (2,3)
- una permutazione identica (id)
Esempio 2
Il numero intero 4 ha le seguenti partizioni.
- 4
- 3+1
- 2+2
- 2+1+1
- 1+1+1+1
Quindi, il gruppo di permutazioni S4 è composto dalle seguenti classi:
- 4-ciclo = ad esempio (1,2,3,4)
- 3-ciclo = ad esempio (1,3,4) , (1,4,2)
- due 2-cicli = ad esempio (1,2)·(3,4)
- un 2-ciclo
- una permutazione identica (id)
E così via.
