Il grado di un vertice in un grafo
In un grafo il grado di un vertice è il numero di spigoli (lati) che sono collegati al vertice stesso.
Un esempio pratico
Ad esempio, in questo grafo il vertice A ha un grado uguale a 3 perché ci sono tre ci sono tre lati collegati (e1, e2, e3).
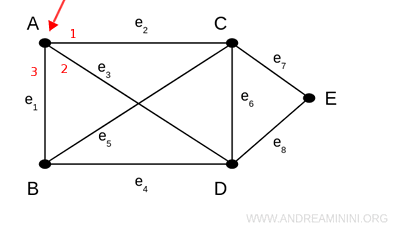
Il vertice E, invece, ha un grado uguale a 2 perché ci sono solo due lati collegati (e7, e8).
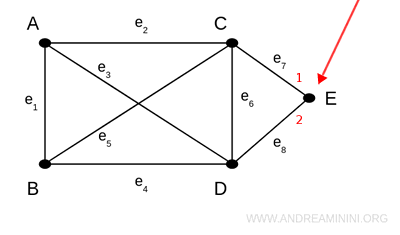
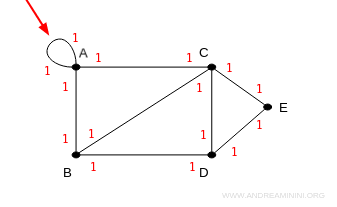
Se il grafico presenta dei loop, ovvero dei cappi, questi vanno contati due volte.
Ad esempio, in questo grafo il vertice A presenta un cappio, ovvero un lato che collega A con se stesso.
Il vertice A ha grado 4 perché ci sono due lati incidenti e un cappio che vale per due lati.
La sequenza dei gradi
La sequenza dei lati è una lista con i gradi del grafo ordinati in modo crescente.
Esempio
In questo grafo ho scritto i gradi di ogni vertice.
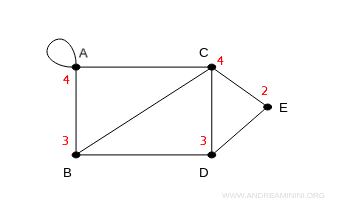
La sequenza dei gradi si ottiene scrivendo i gradi in ordine crescente, dal più piccolo (2) al più grande (4)
$$ \{ 2 , 3, 3, 4, 4 \} $$
La somma dei gradi dei vertici è un numero pari
In ogni grafo la somma dei gradi dei vertici è un numero pari.
Questo teorema è anche conosciuto come "lemma della stretta di mani" perché se diverse persone si stringono la mano, ogni stretta di mano coinvolge due mani.
Dimostrazione
In un grafo ogni lato (spigolo) collega due vertici.
Ad esempio, il lato e1 collega i vertici A e B, il lato e2 collega i vertici A e C, ecc.
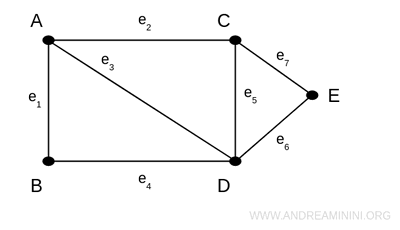
Quindi, la somma dei gradi di tutti i vertici del grafo è uguale al doppio del numero dei lati del grafo stesso.
Essendo il doppio di un numero, allora è sicuramente un numero pari.
E così via.
