Grafi connessi e disconnessi
Un grafo è detto grafo connesso se ogni vertice è raggiungibile da ogni altro vertice. In caso contrario, il grafo è detto grafo disconnesso.
In altre parole, un grafo connesso si presenta in un unico blocco.
Per ogni coppia di vertici del grafo, esiste un cammino che permette di spostarsi da uno all'altro.
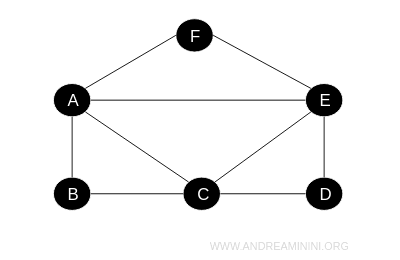
Viceversa, un grafo disconnesso si presenta suddiviso in due o più blocchi separati tra loro.
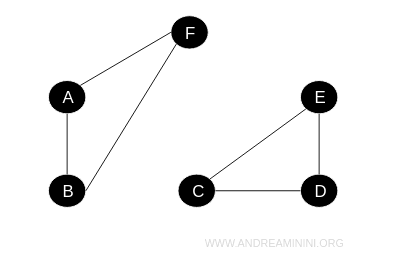
In termini più formali, un grafo disconnesso contiene almeno due vertici tali che non esiste alcun cammino tra di loro.
Questo significa che il grafo disconnesso può essere suddiviso in due o più "blocchi" o componenti, ognuno dei quali è connesso internamente ma isolato dagli altri.
Inoltre, un grafo disconnesso posso vederlo come l'unione di due o più grafi disgiunti.
Dove per unione intendo l'unione degli insiemi dei vertici V(G1)∪V(G2) e l'unione delle famiglie di lati E(G1)∪(EG2)
$$ V(G_1) \cup V(G_2) $$
$$ E(G_1) \cup E(G_2) $$
Viceversa, un grafo connesso non posso rappresentarlo come unione di grafi disgiunti.
Ad esempio, questo grafo disconnesso

Posso vederlo come l'unione di due grafi disgiunti. L'unione degli insiemi dei vertici $$ \{ A, B, F \} \cup \{ C, D, E \} $$ e l'unione delle famiglie dei lati $$ \{ (A,B), (A,F), (B,F) \} \cup \{ (C, D), (C,E), (D,E) \} $$
La connettività di un grafo è quindi una misura della sua coesione interna e della capacità di permettere flussi o movimenti all'interno della sua struttura.
Come capire se un grafo è connesso?
Per analizzare la connettività di un grafo, gli algoritmi possono esplorare la struttura partendo da un vertice e cercando di raggiungere tutti gli altri vertici seguendo i cammini disponibili.
Se l'esplorazione riesce a toccare tutti i vertici partendo da qualsiasi vertice di partenza, il grafo è connesso.
In caso contrario, l'analisi rivela le diverse componenti connesse del grafo.
Un esempio pratico
Considero un insieme di quattro città A, B, C, D collegate da strade.
In questa rete, ogni città è collegata ad almeno un'altra città, ed è possibile viaggiare da qualsiasi città a qualsiasi altra città attraverso una serie di strade.
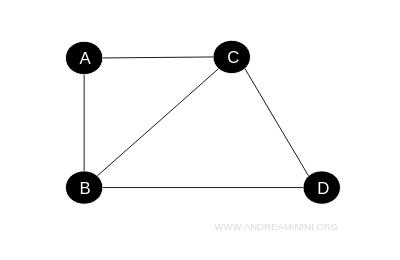
In questo caso
- A è collegata a B e C
- B è collegata a C e D
- C è collegata a D
In questo esempio, nonostante non tutte le città siano collegate direttamente tra loro, esiste sempre un percorso che permette di raggiungere qualsiasi città partendo da qualsiasi altra città.
Questo è un esempio pratico di grafo connesso.
Ad esempio, A e D non sono collegate direttamente ma esiste un cammino per andare da A a D e viceversa, passando per B oppure per C.
Esempio 2
Considero un gruppo di isole dove alcune isole sono collegate da ponti, ma altre sono completamente isolate.
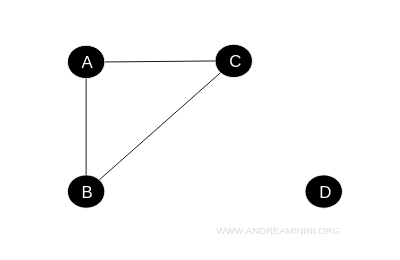
In questo caso, ci sono quattro isole A, B, C, e D, con le seguenti connessioni:
- A è collegata a C e a B
- B è collegata C
- D è isolata.
In questa situazione, non esiste modo di raggiungere l'isola D in automobile partendo dalle isole A, B o C, e viceversa.
L'isola D forma una componente separata dal resto del grafo e il grafo è suddiviso in due parti.
Questo è un esempio pratico di grafo disconnesso.
E così via.
