Grafi isomorfi

Due grafi sono isomorfi se uno può essere trasformato nell'altro semplicemente rinominando i suoi vertici, senza modificare la struttura di connessione tra di essi.

Pur avendo rappresentazioni visive diverse, i grafi isomorfi hanno una corrispondenza uno-a-uno tra i loro vertici tale che le connessioni (o archi) tra i vertici in un grafo corrispondono esattamente alle connessioni tra i vertici corrispondenti nell'altro grafo.

L'isomorfismo tra grafici è un concetto chiave nella teoria dei grafi, perché permette di classificare i grafici in base alla loro struttura, indipendentemente da come sono disegnati o rappresentati. Questo concetto è particolarmente utile in vari campi come la chimica, per la modellazione di molecole, in informatica, per la verifica di circuiti e reti, e in matematica, per lo studio delle proprietà strutturali dei grafici.

Un esempio pratico

Ad esempio, questi due grafi sono isomorfi, perché hanno gli stessi vertici e gli stessi lati/adiacenze.

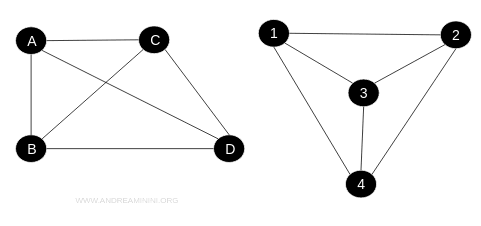
Il numero di lati che collegano una coppia di vertici nel grafico G1 corrisponde esattamente al numero di lati che collegano la coppia di vertici corrispondente nel grafico G2.

Come capire se due grafi sono isomorfi

Per determinare se due grafici sono isomorfi, devo cercare una funzione biunivoca (una corrispondenza uno-a-uno) tra i set di vertici dei due grafi che preservi le adiacenze.

Ciò significa che se due vertici sono connessi da un arco in un grafo, i loro corrispondenti vertici devono essere connessi da un arco nel secondo grafo.

Nota. Se i grafi hanno pochi vertici e lati, una tecnica consiste nel togliere le etichette ai grafi, cercare le somiglianze e assegnare nuove etichette comuni, partendo dai vertici con più adiacenze (lati) ovvero da quelli con grado maggiore. In altre parole, dati due grafi senza etichette nei vertici, cerco di assegnargli delle etichette in modo tale che diventino grafi isomorfi. Questo perché, togliendo le etichette si riducono le combinazioni possibili da analizzare. Ad esempio, se considero 3 vertici etichettati, ci sono 8 combinazioni possibili per connetterli.

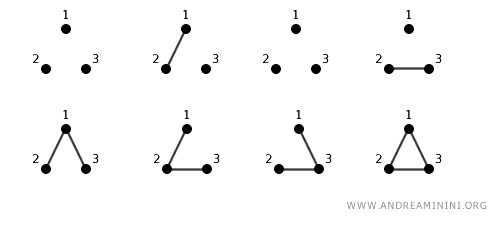
Togliendo le etichette, le combinazioni possibili tra i tre vertici "non etichettati" si riducono a quattro. Pertanto, senza etichette il confronto tra due grafi diventa più facile.

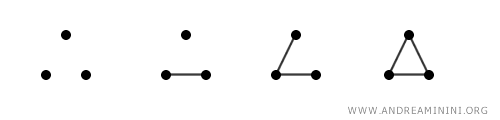
Questo processo può essere impegnativo dal punto di vista computazionale, in particolar modo se i grafi sono molto grandi.

Le proprietà dei grafi isomorfi

Quando due grafi sono isomorfi, condividono le stesse proprietà strutturali. Ecco una sintesi delle principali proprietà preservate:

• Numero di vertici e archi
  Due grafi isomorfi hanno lo stesso numero di vertici e di archi.
• Grado dei vertici
  Ogni vertice mantiene lo stesso grado nei due grafi.
• Sottografi
  Ogni sottografo di uno corrisponde a un sottografo isomorfo nell'altro.
• Cicli e cammini
  I cicli e i cammini sono preservati, con le stesse lunghezze in entrambi i grafi isomorfi.
• Connettività
  Se un grafo è connesso, anche l'altro lo è.
• Complementi
  I complementi di due grafi isomorfi sono anch'essi isomorfi.

Queste proprietà rendono i grafi isomorfi strutturalmente identici, nonostante possano apparire diversi.

Note

Alcune note a margine sull'isomorfismo tra grafi.

• Classe di isomorfismo
  Due o più grafi isomorfi tra loro appartengono alla stessa classe di isomorfismo. In genere, quando si discute di un grafo senza nominare i vertici specifici, spesso ci si riferisce alla sua classe di isomorfismo. 

  Ad esempio, tutti i percorsi con n vertici sono reciprocamente isomorfi e formano una classe di isomorfismo.

• La relazione di isomorfismo è una relazione di equivalenza
  Questo significa che è riflessiva, simmetrica e transitiva:
  • Riflessiva: Ogni grafo è isomorfo a se stesso.
  • Simmetrica: Se \( G \) è isomorfo a \( H \) (\( G \cong H \)), allora \( H \) è isomorfo a \( G \) (\( H \cong G \)).
  • Transitiva: Se \( G \) è isomorfo a \( H \) (\( G \cong H \)) e \( H \) è isomorfo a \( F \) (\( H \cong F \)), allora \( G \) è isomorfo a \( F \) (\( G \cong F \)).

E così via