Grafi hamiltoniani
Un grafo viene detto "hamiltoniano" quando è possibile tracciare un percorso che visita ogni vertice esattamente una volta e termina nel vertice da cui è iniziato.
Analogamente, un digrafo si considera "hamiltoniano" se esiste un percorso orientato che percorre ogni nodo del digrafo una sola volta, per poi tornare al nodo da cui è partito.
Un esempio pratico
Questo grafo è classificato come hamiltoniano perché è possibile individuare un percorso che attraversa una volta ciascun vertice del grafo.
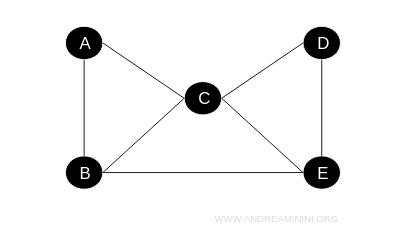
Un cammino hamiltoniano è il seguente:
$$ A \rightarrow B \rightarrow E \rightarrow D \rightarrow C \rightarrow A $$
Il percorso ha origine e finisce nello stesso vertice (B) e tocca tutti i vertici del grafo.
Nota. Da sottolineare che, in un grafo hamiltoniano, non è richiesto che il cammino attraversi una sola volta ogni spigolo. Ciò che è fondamentale è che ogni vertice venga visitato una e una sola volta.
Esempio 2
Questo digrafo è hamiltoniano poiché è presente un percorso che parte e si conclude sullo stesso nodo, attraversando una singola volta tutti i nodi del digrafo.
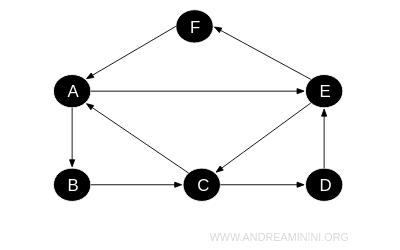
Un cammino hamiltoniano nel digrafo è il seguente:
$$ A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A $$
Anche in questo caso, non è indispensabile che il percorso hamiltoniano attraversi ogni arco una sola volta.
L'importante è che il percorso abbia inizio e fine nello stesso nodo, identificato come A, e che ogni nodo venga percorso una sola volta.
E così via.
