Grafi eureliani

Un grafo è detto "eureliano" se esiste un percorso che include ogni spigolo una e una sola volta e termina nel vertice iniziale del cammino.

Allo stesso modo, un digrafo hamiltoniano è un grafo orientato in cui esiste un cammino che comprende ogni nodo una sola volta e termina nel nodo iniziale del cammino.

Un esempio pratico

Questo grafo è un grafo hamiltoniano perché esiste un cammino che passa una sola volta per tutti i vertici del grafo.

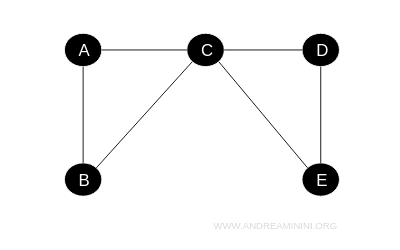
Un cammino hamiltoniano è il seguente:

$$ B \rightarrow A \rightarrow C \rightarrow D \rightarrow E \rightarrow C \rightarrow B $$

Il cammino inizia e termina allo stesso nodo (B) e passa per tutti i vertici del grafo.

Nota. In un grafo hamiltoniano non occorre che il cammino passi una sola volta anche per gli spigoli. E' necessario che passi una sola volta per i vertici.

Esempio 2

Questo digrafo è hamiltoniano perché esiste un cammino che inizia e termina allo stesso nodo e passa una sola volta per tutti i nodi del digrafo.

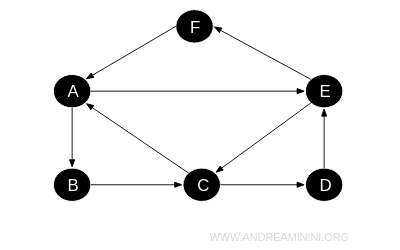
Un cammino hamiltoniano è il seguente:

$$ A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A $$

Anche in questo caso non è necessario che il digrafo eureliano passi una sola volta per gli archi.

Ciò che conta è che inizi e termini dallo stesso nodo (A) e passi una sola volta per tutti i nodi.

E così via.