Come calcolare l'angolo di due piani incidenti

Il coseno dell'angolo di due piani incidenti nello spazio è determinato dal rapporto tra il prodotto scalare dei vettori direttori <v₁,v₂> e il prodotto delle norme dei vettori direttori ||v₁||·||v₂||. $$ cos(α) = \frac{<v_1,v_2>}{||v_1|| \cdot ||v_2||} $$

Al posto dei vettori direttori posso usare anche i vettori normali.

Il risultato è il coseno dell'angolo α dei due piani.

Una volta trovato, basta calcolare l'arcocoseno per ottenere l'ampiezza dell'angolo alfa.

$$ α = arccos(\cos α) $$

Poiché i piani formano due coppie di angoli opposti al vertice, quando si conosce alfa è possibile calcolare l'altro angolo per differenza.

$$ π-α $$

Nota. Se sono paralleli non formano una coppia di angoli. In questi casi, per definizione si assegna alle coppie di angoli α=0 e π-α=∞.

Se il prodotto scalare è nullo <v₁,v₂>, i due piani sono ortogonali.

Esempio

Ho due piani incidenti

$$ 2x + 3y + z = 0 $$

$$ -3x -4y -5z = 0 $$

Ecco i due piani sul diagramma cartesiano.

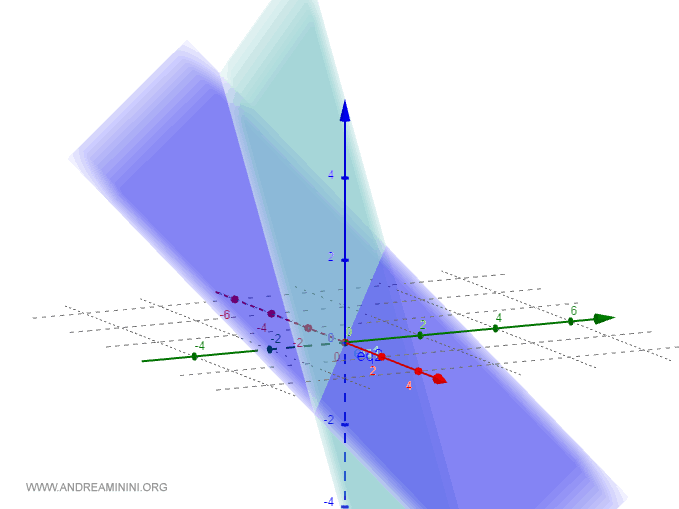
Calcolo le coppie degli angoli formate dai due piani:

$$ cos(α) = \frac{<v_1,v_2>}{||v_1|| \cdot ||v_2||} $$

In questo caso i piani sono rappresentati da equazioni cartesiane.

Posso usare i vettori normali al posto dei vettori direttori.

Essendo ortogonali ai vettori direttori, il risultato non cambia.

$$ cos(α) = \frac{<n_1,n_2>}{||n_1|| \cdot ||n_2||} $$

I vettori normali dei due piani sono:

$$ n_1 = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} -3 \\ -4 \\ -5 \end{pmatrix} $$

Quindi, il coseno dell'angolo è

$$ cos(α) = \frac{ 2 \cdot (-3) + 3 \cdot (-4) + 1 \cdot (-5) }{ \sqrt{2^2+3^2+1^2} \cdot \sqrt{(-3)^2+(-4)^2+(-5)^2} } $$

$$ cos(α) = \frac{ -23 }{ \sqrt{14} \cdot \sqrt{50} } $$

$$ cos(α) = -0.8315 $$

Ho trovato il coseno dell'angolo alfa.

A questo punto calcolo l'arcocoseno per conoscere l'ampiezza dell'angolo in radianti.

$$ α =arccos(-0.8315) = 2.552 π $$

L'angolo α misura 2.552 radianti ( circa 146° ).

Poi calcolo per differenza l'altro angolo.

$$ π-α = 3.14 - 2.552 = 0.588 π $$

L'angolo supplementare π-α misura 0.588 radianti ( circa 34° ).

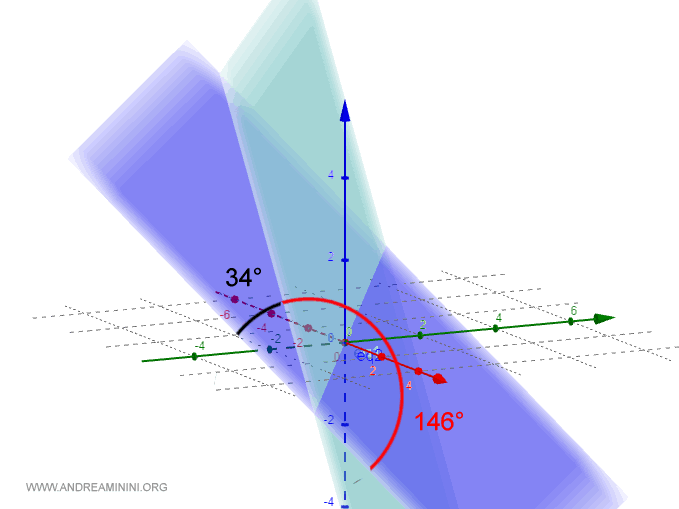
E così via.