Esercizio studio di funzione 10
In questo esercizio studio la funzione esponenziale usando gli strumenti dell'analisi matematica
$$ f(x)= e^{ - \frac{1}{x}} $$
Dominio
La funzione è definita nell'insieme dei numeri reali ad eccezione che in x=0.
$$ D_f = R - \{ 0 \} $$
In x=0 si verifica una divisione per zero nelll'esponente (1/x).
Pertanto, x=0 è un punto indefinito della funzione.
Intercette
A questo punto verifico le intercette quando x=0 e y=0.
- Intercetta con l'asse y
Sapendo che x=0 è un punto indefinito della funzione, posso già dedurre che non esiste l'intercetta con l'asse delle ordinate. - Intercetta con l'asse x
Per verificare se esiste l'intercetta con l'asse x devo provare a risolvere l'equazione f(x)=0 ossia $$ e^{ - \frac{1}{x}} = 0 $$ Utilizzo la proprietà invariantiva delle equazioni per applicare il logaritmo naturale a entrambi i membri. Il logaritmo naturale è la funzione inversa dell'esponenziale. In questo modo posso eliminare l'esponenziale dal membro sinistro dell'equazione. $$ \log ( e^{ - \frac{1}{x}} ) = \log( 0 ) $$ $$ - \frac{1}{x} = \log( 0 ) $$ Sapendo che il logaritmo naturale non è definito in zero, deduco che l'equazione non ha soluzioni. Quindi, non esiste l'intercetta con l'asse delle ascisse.
Ricapitolando, la funzione non interseca né l'asse x, né l'asse y.
Studio del segno
In questo caso lo studio del segno della funzione è abbastanza semplice.
La funzione esponenziale è una funzione positiva per qualsiasi numero reale.
Quindi, la funzione f(x)=e-1/x è sempre positiva.
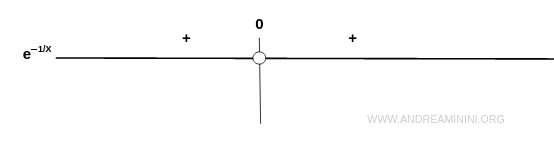
Questo mi permette di dedurre che la funzione non passa per il III e il IV quadrante del diagramma cartesiano.
Asintoti verticali
Essendoci un punto indefinito, studio il limite desto e sinistro intorno a x=0 per verificare se esiste un asintoto verticale.
Quando x tende a zero da sinistra (x→0-), il valore -1/x diventa negativamente infinito, quindi e(-1/x) diventa e(-∞), che è uguale a 0.
$$ \lim_{x \rightarrow 0^-} e^{ - \frac{1}{x}} = 0$$
Come x tende a zero da destra (x→0+), il valore -1/x diventa positivamente infinito, quindi e(-1/x) diventa e(∞), che è essenzialmente infinito.
$$ \lim_{x \rightarrow 0^+} e^{ - \frac{1}{x}} = \infty $$
Quindi, il limite della funzione e(-1/x) come x tende a zero non esiste, poiché i limiti da sinistra e da destra non coincidono.
Posso però già fissare la tendenza del grafico della funzione intorno a x=0.
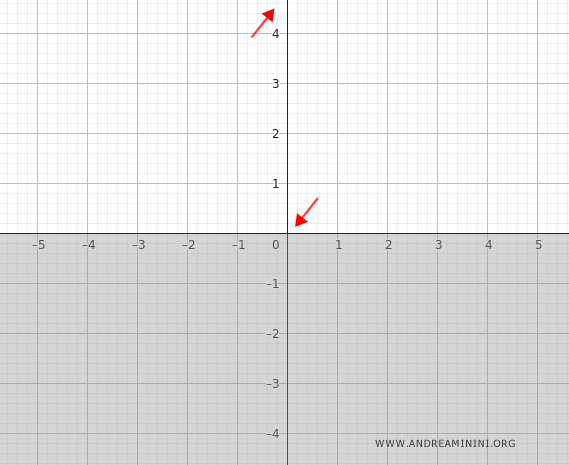
Asintoti orizzontali
A questo punto analizzo il comportamento asintotico della funzione per x che tende a più infinito e a meno infinito.
Per x che tende a +∞ la funzione f(x) tende a 1
$$ \lim_{x \rightarrow \infty } e^{ - \frac{1}{x}} = \lim_{x \rightarrow \infty } \frac{1}{ e^{ \frac{1}{x} } } = \frac{1}{1} = 1^+ $$
Spiegazione. Quando x è infinitamente grande, 1/x è un valore positivo infinitesimale vicino a zero (0+). Sapendo che e0=1, il risultato del limite è intuitivo. Inoltre, per x=0+ la funzione e0+ è maggiore di 1. Pertanto 1/e0+=1/1+ è minore di 1. Quindi, la funzione f(x) tende a 1 dal basso.
Per x che tende a -∞ la funzione f(x) tende a +∞
$$ \lim_{x \rightarrow - \infty } e^{ - \frac{1}{x}} = \lim_{x \rightarrow \infty } \frac{1}{ e^{ \frac{1}{x} } } = \frac{1}{1} = 1 $$
Spiegazione. Quando x tende a meno infinito, 1/x è un valore infinitesimale negativo vicino a zero (0-). Sapendo che e0=1, il risultato del limite è intuitivo. Inoltre, per x=0- la funzione e0- è minore di 1. Pertanto 1/e0-=1/1- è maggiore di 1. Quindi, la funzione f(x) tende a 1 dall'alto.
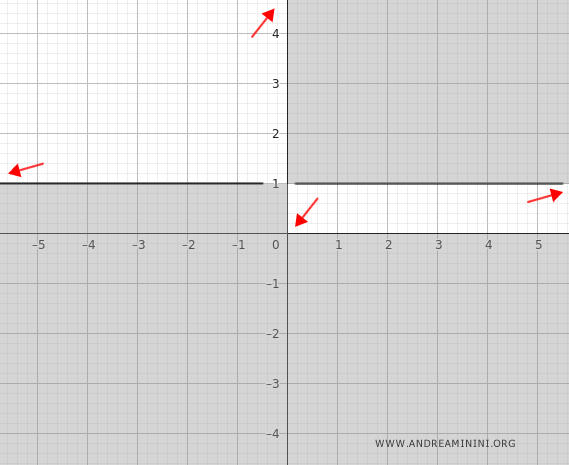
Pertanto la funzione ha un asintoto orizzontale in y=1.
Aggiungo questo ulteriore mattoncino alla costruzione del grafico.
Crescenza e decrescenza
Per studiare la crescenza e la decrescenza della funzione, devo calcolare la sua derivata prima.
$$ f'(x) = D_x[ e^{ - \frac{1}{x}} ] $$
Nel caso dell'esponenziale, devo eseguire la derivazione di una funzione composta.
$$ f'(x) = e^{ - \frac{1}{x}} \cdot D_x[-\frac{1}{x}] $$
$$ f'(x) = e^{ - \frac{1}{x}} \cdot D_x[-x^{-1}] $$
$$ f'(x) = e^{ - \frac{1}{x}} \cdot [ -1 \cdot - (x^{-2} ) ] $$
$$ f'(x) = x^{-2} \cdot e^{ - \frac{1}{x}} $$
Una volta ottenuta la derivata prima, ne studio il segno.
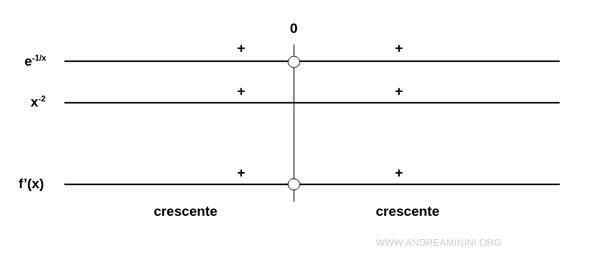
La derivata prima è sempre positiva. Quindi, la funzione è sempre crescente in ogni punto del suo dominio.
Aggiorno il grafico per indicare questo comportamento, ancora grezzo, della funzione.
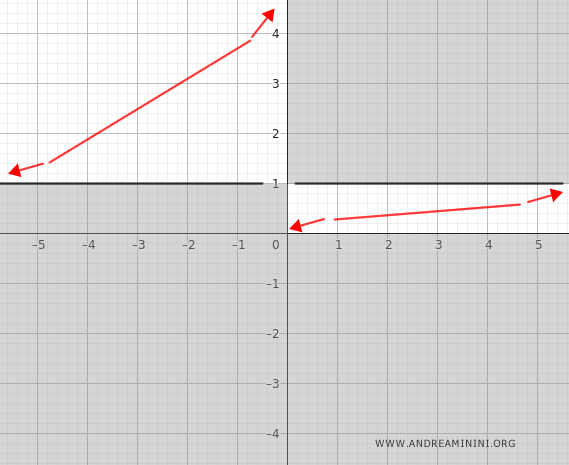
Convessità e concavità
Resta solo da capire in quali tratti la funzione è convessa e in quali è concava.
Per studiare quest'ultima caratteristica devo calcolare la derivata seconda della funzione, ossia la derivata della derivata prima
$$ f''(x) = D_x[ f'(x) ] $$
$$ f''(x) = D_x[ x^{-2} \cdot e^{ - \frac{1}{x}} ] $$
In questo caso utilizzo la formula di derivazione del prodotto di due funzioni.
$$ f''(x) = D_x[x^{-2}] \cdot e^{ - \frac{1}{x}} + x^{-2} \cdot D [e^{ - \frac{1}{x}} ] $$
$$ f''(x) = -2 x^{-3} \cdot e^{ - \frac{1}{x}} + x^{-2} \cdot x^{-2} \cdot e^{ - \frac{1}{x}} $$
$$ f''(x) = -2 x^{-3} \cdot e^{ - \frac{1}{x}} + x^{-4} \cdot e^{ - \frac{1}{x}} $$
Fattorizzo il risultato per studiare più agevolmente il segno della derivata seconda.
$$ f''(x) = e^{ - \frac{1}{x}} \cdot ( -2 x^{-3} + x^{-4} ) $$
$$ f''(x) = e^{ - \frac{1}{x}} \cdot [ x^{-3} \cdot (-2 + x^{-1} ) ] $$
$$ f''(x) = e^{ - \frac{1}{x}} \cdot [ x^{-3} \cdot (-2 + \frac{1}{x} ) ] $$
$$ f''(x) = e^{ - \frac{1}{x}} \cdot [ x^{-3} \cdot \frac{1-2x}{x} ] $$
A questo punto posso studiare il segno della derivata seconda della funzione.
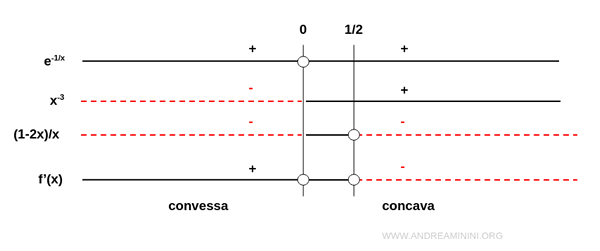
Nota. Lo studio del segno del rapporto (1-2x)/x si svolge risolvendo la disequazione fratta (1-2x)/x > 0 $$ \frac{1-2x}{x} > 0 $$ La condizione di esistenza è x≠0. Il numeratore (1-2x) del rapporto è positivo per ogni x<1/2 mentre il denominatore (x) è positivo per ogni x>0. Quindi, il rapporto è positivo nell'intervallo 0<x<1/2.
La derivata seconda è positiva per ogni x<1/2 e negativa per ogni x>1/2.
Pertanto, la funzione è convessa nell'intervallo (-∞, 1/2) e concava nell'intervallo (1/2, +∞).
Inoltre, nel punto x=1/2 la derivata seconda passa da positiva a negativa, quindi in x=1/2 la funzione ha un flesso discendente.
Queste informazioni mi permettono di completare il grafico della funzione.
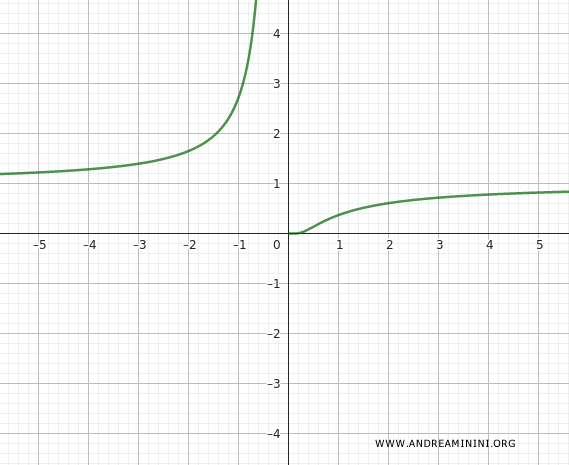
E così via.
