Esercizio studio della funzione 1
In questo esercizio studio la funzione $$ f(x) = \frac{x+1}{x-1} $$
Disegno il diagramma cartesiano vuoto
Per prima cosa individuo studio il campo di definizione della funzione.
La funzione è definita nell'insieme dei numeri reali ad eccezione di x=1.
$$ (-∞,1)∪(1,+∞) $$
Poi individuo le intercette della funzione f(x) con gli assi x e y.
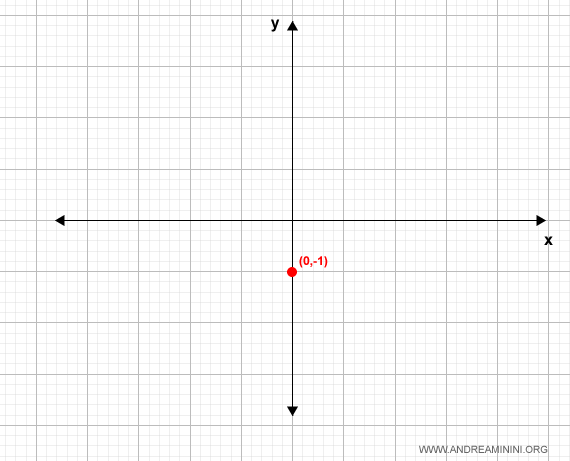
Se x=0 il valore di y è -1
$$ f(0) = \frac{0+1}{0-1} = -1 $$
Quindi la funzione passa per il punto (0,-1).
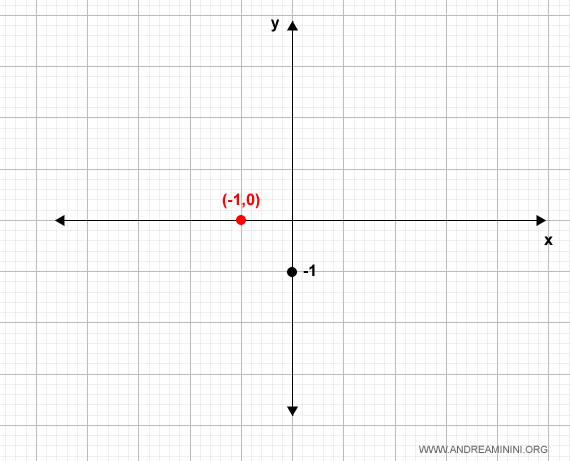
Poi verifico se e in quali condizioni la f(x)=0
In questo caso il rapporto diventa nullo per x=-1
$$ \frac{x+1}{x-1} = 0 $$
Quindi la funzione passa per il punto (-1,0).
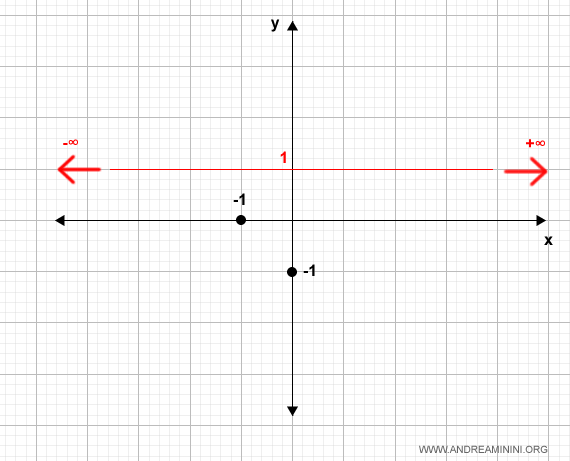
Studio il limite della funzione per x tendente a più e meno infinito.
$$ \lim_{x \rightarrow \infty} \frac{x+1}{x-1} = \frac{∞}{∞} $$
$$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = \frac{∞}{∞} $$
Essendo limiti in forma indeterminata del tipo ∞/∞ applico il teorema di De L'Hopital.
Entrambi i limiti tendono a 1.
$$ \lim_{x \rightarrow \infty} \frac{x+1}{x-1} = 1 $$
$$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$
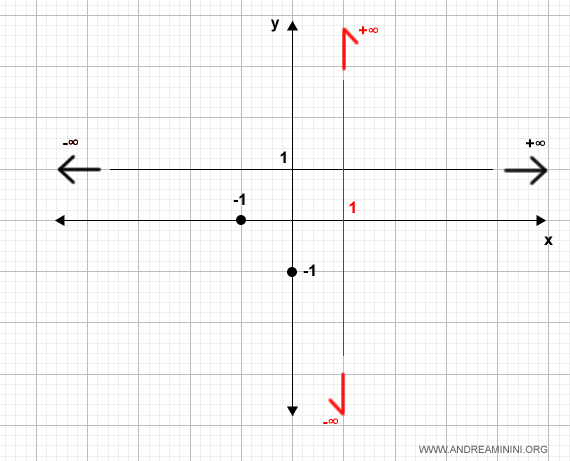
Aggiungo il risultato dei limiti sul diagramma cartesiano
Ora verifico se la funzione ha dei punti indefiniti, ossia dei punti in cui il valore della funzione non può essere definito.
La funzione non è definita per x=1 perché il denominatore diventa zero.
$$ f(1) = \frac{x+1}{x-1} = \frac{1+1}{1-1} = \frac{2}{0} $$
Nei punti indefiniti la funzione ha un asintoto verticale.
Studio il limite destro e sinistro della funzione per x tendente a 1 per capire l'andamento della funzione..
$$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} =+∞ $$
$$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = -∞ $$
Nel punto x=1 la funzione f(x) tende a -∞ da sinistra e +∞ da destra.
Aggiorno il diagramma cartesiano con quest'altra informazione.
Ora studio il segno della funzione nel suo campo di definizione (-∞,1)∪(1,+∞)
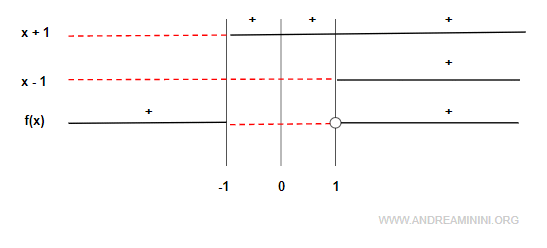
La funzione è positiva nell'intervallo (-∞,-1) e (1,+∞). E' invece negativa nell'intervallo (-1, 1).
Utilizzo queste informazioni per eliminare i quadranti e le sezioni in cui la funzione non passa (zone grigie).
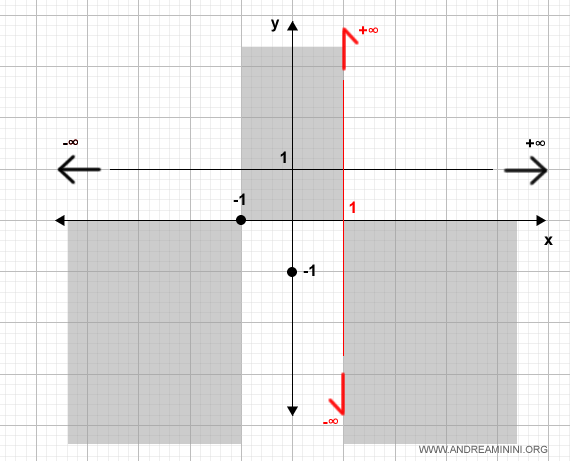
Ora calcolo la derivata prima della funzione
$$ f'(x) = \frac{(x-1) - (x+1)}{(x-1)^2} = \frac{-2}{(x-1)^2} $$
Analizzo il segno della derivata prima nel campo di definizione (-∞,-1) e (1,+∞) per studiare la crescenza e la decrescenza della funzione.
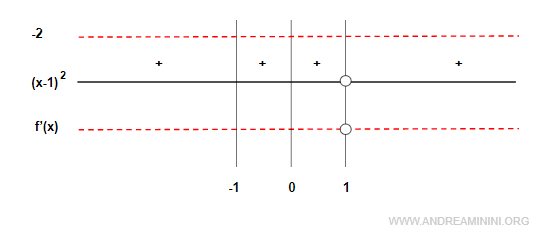
La derivata prima f'(x) è negativa in tutto il campo di definizione. Quindi, la funzione è sempre decrescente.
Questo mi permette approssimare il grafico della funzione unendo i punti di passaggio sul diagramma.
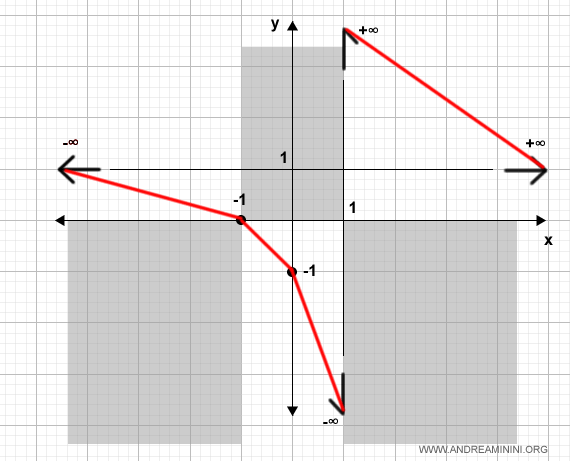
Ora calcolo la derivata seconda della funzione
$$ f''(x) = \frac{0 - (-2)(2(x-1)) }{(x-1)^4} = \frac{ 4(x-1) }{(x-1)^4} = \frac{ 4 }{(x-1)^3} $$
Analizzo il segno della derivata seconda nel campo di definizione (-∞,-1) e (1,+∞) per studiare la convessità e la concavità della funzione.
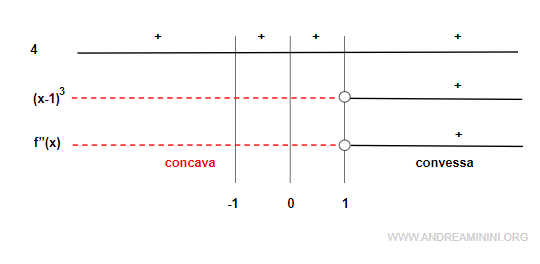
Nell'intervallo (-∞,1) in cui la derivata seconda è negativa la funzione è concava .
Nell'intervallo (1,∞) in cui la derivata seconda è positiva la funzione è convessa.
Aggiorno il grafico con quest'ultima informazione.
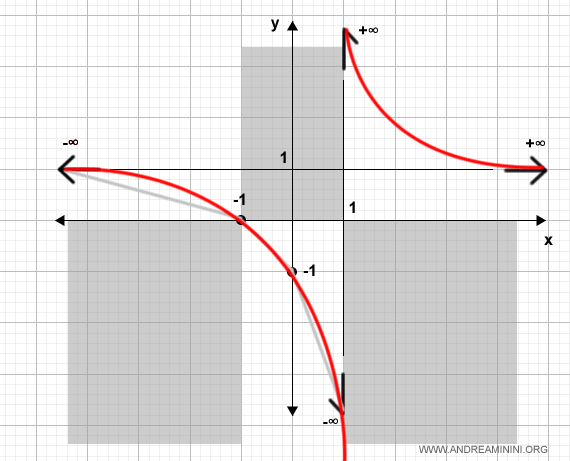
Con questa informazione ho completato lo studio della funzione.
Il grafico è completo.
Verifica. Il grafico della funzione realizzato con Geogebra.
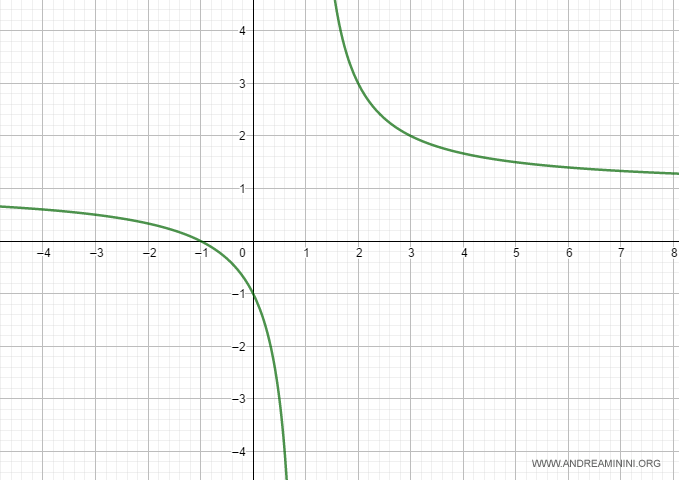
E così via.
