Esercizio studio della funzione 2
Devo studiare il grafico della funzione
$$ f(x) = \frac{x-1}{x+1} $$
Dominio
La funzione è definita nell'intervallo
$$ D_f = (-\infty, 1) \cup (1, \infty) \ \ \ \forall \ x \in R $$
Studio del segno
La funzione è positiva negli intervalli (-∞,-1) ∪ (1,∞) ed è negativa nell'intervallo (-1,1)
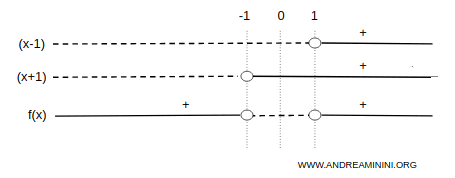
Questo mi permette di escludere le zone del piano in cui la funzione non passa (in grigio).
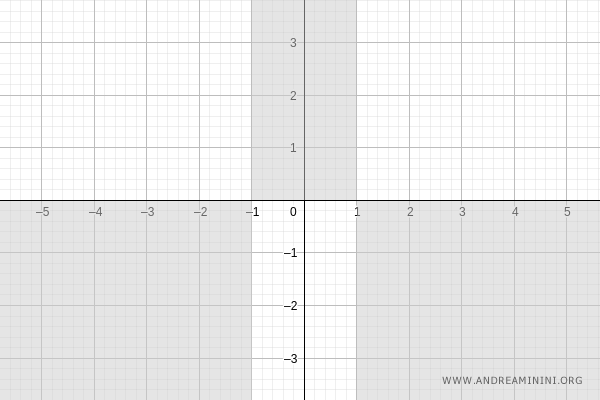
Punti indefiniti
La funzione non è definita in x=-1 perché si annulla il denominatore.
In questo punto potrebbe esserci un asintoto verticale.
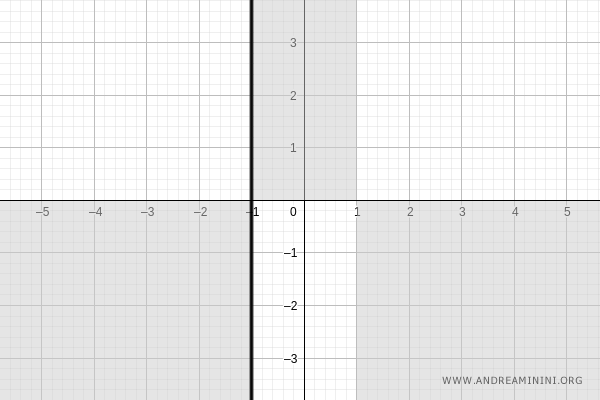
Calcolo il limite destro e sinistro per x→-1.
$$ \lim_{x \rightarrow -1^-} \frac{x-1}{x+1} = + \infty $$
$$ \lim_{x \rightarrow -1^+} \frac{x-1}{x+1} = - \infty $$
Nell'intorno di x=-1 la funzione tende a più infinito a sinistra e meno infinito a destra.
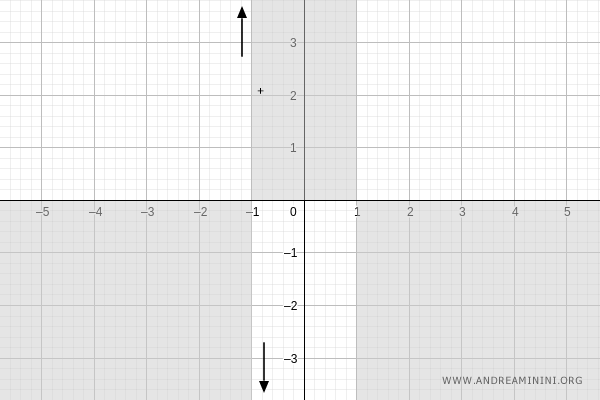
Le intercette con gli assi
Per x=0 la funzione assume il valore y = -1.
$$ f(x) = \frac{x-1}{x+1} = \frac{0-1}{0+1} = f(x) = \frac{-1}{1} = -1 $$
Quindi la funzione passa per il punto (x,y)=(0,-1).
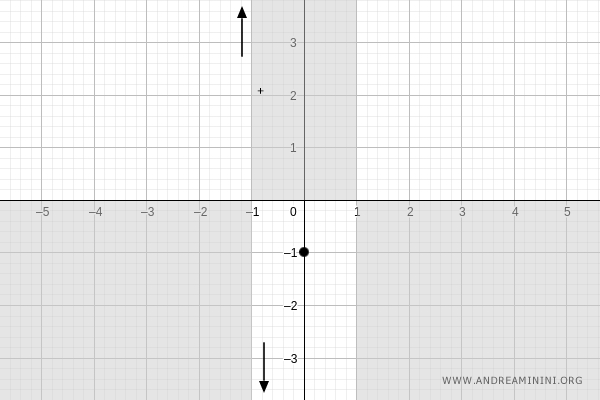
Per y=0 la funzione assume il valore x=1
$$ \frac{x-1}{x+1} = 0 $$
$$ x-1 = 0 $$
$$ x = 1 $$
Quindi la funzione passa anche per il punto (x,y)=(1,0).
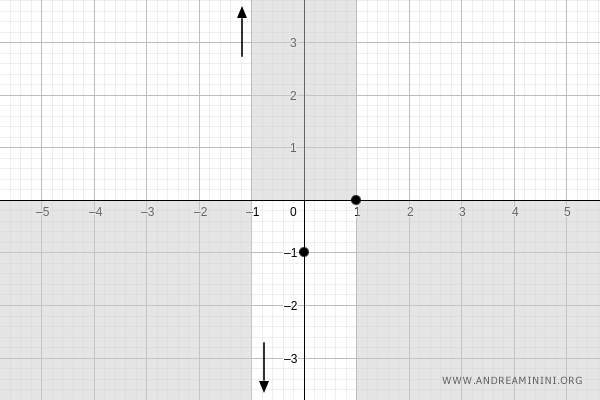
Asintoti orizzontali
Calcolo il limite della funzione per x→+∞
$$ \lim_{x \rightarrow + \infty } \frac{x-1}{x+1} = \frac{\infty}{\infty} $$
Il limite è una forma indeterminata ∞/∞
Per studiare il limite applico il teorema di De L'Hopital.
$$ \lim_{x \rightarrow + \infty } \frac{D[x-1]}{D[x+1]} = \lim_{x \rightarrow + \infty } \frac{1}{1} = 1 $$
Quindi, la funzione tende a y=1 per x→+∞
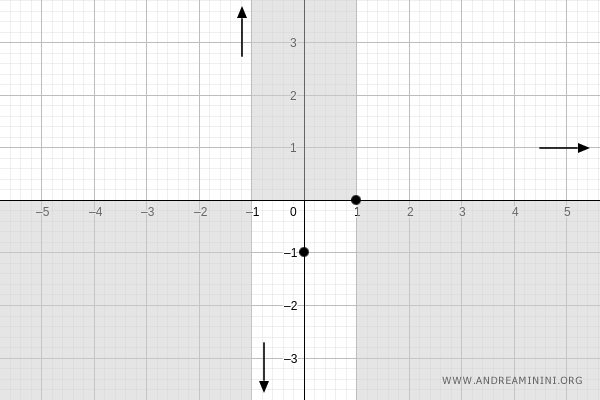
Calcolo il limite della funzione per x→-∞
$$ \lim_{x \rightarrow - \infty} \frac{x-1}{x+1} = \infty $$
Il limite è una forma indeterminata ∞/∞
Per studiare il limite applico il teorema di De L'Hopital.
$$ \lim_{x \rightarrow + \infty } \frac{D[x-1]}{D[x+1]} = \lim_{x \rightarrow + \infty } \frac{1}{1} = 1 $$
Quindi, la funzione tende a y=1 per x→-∞
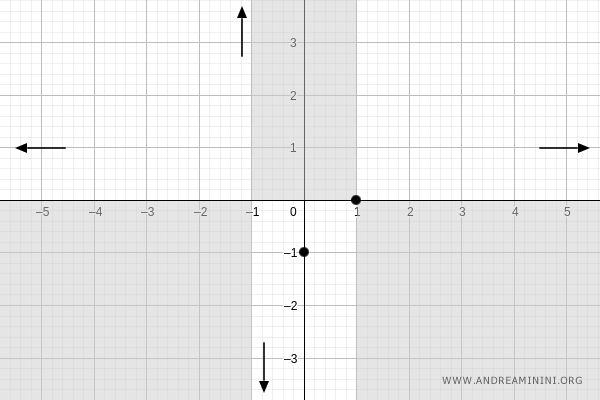
Crescenza e decrescenza
Calcolo la derivata prima della funzione
$$ f'(x) = D[\frac{x-1}{x+1}] = \frac{ (x+1) - (x-1) }{ (x+1)^2 } \frac{ 2 }{ (x+1)^2 } $$
La derivata prima della funzione è positiva per ogni valore della x.
Quindi la funzione è sempre crescente.
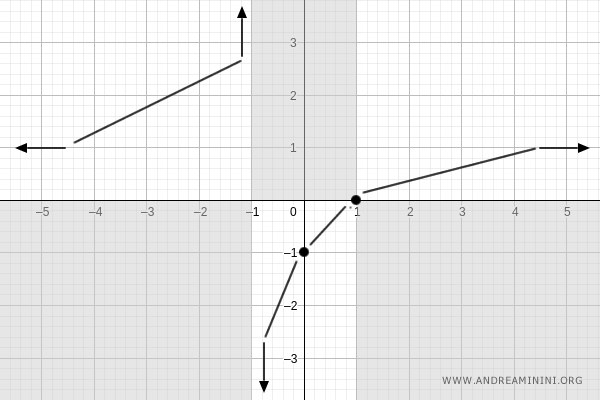
Concavità e convessità
Calcolo la derivata secona della funzione
$$ f''(x) = D''[\frac{x-1}{x+1}] = D[ \frac{ 2 }{ (x+1)^2 } ] = $$
$$ = 2 \cdot D [ (x+1)^{-2} ] = 2 \cdot [ -2 (x+1)^{-3} ] = \frac{-4}{(x+1)^3} $$
La derivata seconda è positiva nell'intervallo (-∞,-1) e negativa nell'intervallo (-1,∞).
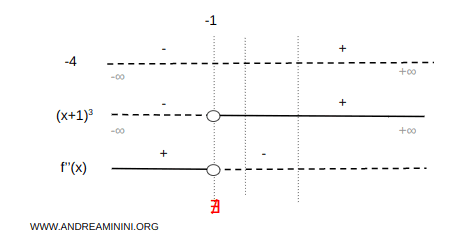
Quindi, la funzione è convessa nell'intervallo (-∞,-1)
E' invece concava nell'intervallo (-1,∞)
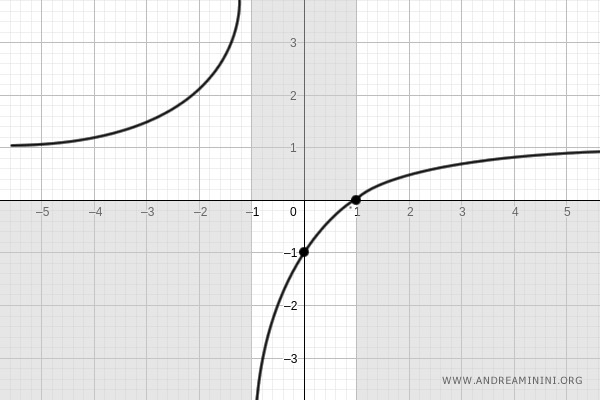
E così via.
