Esercizio studio di funzione 4
Devo studiare il grafico di questa funzione
$$ f(x) = \frac{x}{x^2+2} $$
Dominio
La funzione è definita in tutto l'insieme dei numeri reali.
$$ D_f = (-\infty, \infty) $$
Punti indefiniti
Non ci sono punti in cui la funzione è indefinita perché il denominatore non ha soluzioni reali.
$$ x^2+2 = 0$$
$$ x^2 = -2 $$
Asintoti orizzontali
Studio il comportamento asintotico della funzione per x→+∞ e per x→-∞.
$$ \lim_{x \rightarrow +\infty} \frac{x}{x^2+2} = \frac{\infty}{\infty} = 0^+ $$
$$ \lim_{x \rightarrow -\infty} \frac{x}{x^2+2} \frac{-\infty}{\infty} = 0^- $$
La funzione tende a zero sia per x→+∞ che per x→-∞.
Le intercette con gli assi
Per x=0 la funzione assume il valore 0
$$ f(0) = \frac{0}{0^2+2} = 0 $$
Pertanto, la funzione passa per l'origine (x,y)=(0,0) del piano cartesiano.
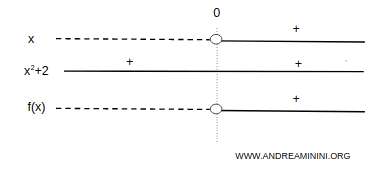
Lo studio del segno
La funzione è negativa nell'intervallo (-∞,0) e positiva nell'intervallo (0,∞).
Questo mi consente di eliminare le aree del piano cartesiano dove non passa il grafico della funzione.
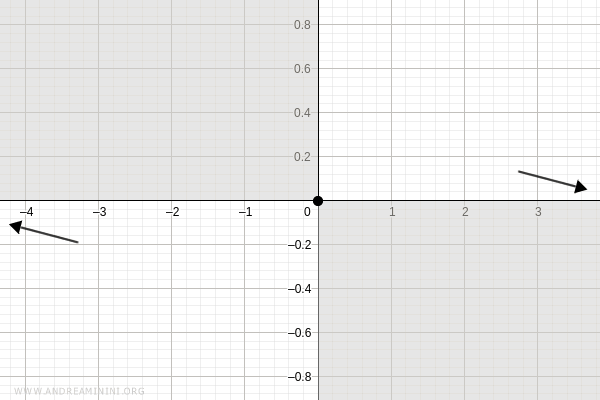
Crescenza e decrescenza
Calcolo la derivata prima della funzione per studiare la crescenza e la decrescenza.
$$ f'(x) = D[ \frac{x}{x^2+2} ] = \frac{(x^2+2)-x(2x)}{(x^2+2)^2} = \frac{x^2-2x^2+2}{(x^2+2)^2} = \frac{-x^2+2}{(x^2+2)^2} $$
Poi studio il segno della derivata prima.
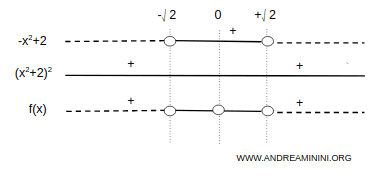
La funzione è decrescente negli intervalli (-∞, -√2) e (√2, +∞).
E' crescente nell'intervallo (-√2, √2).
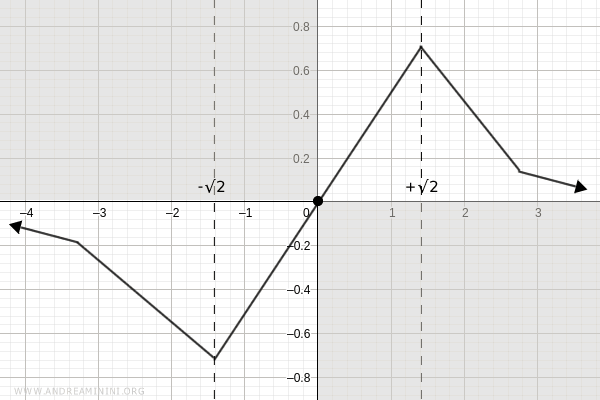
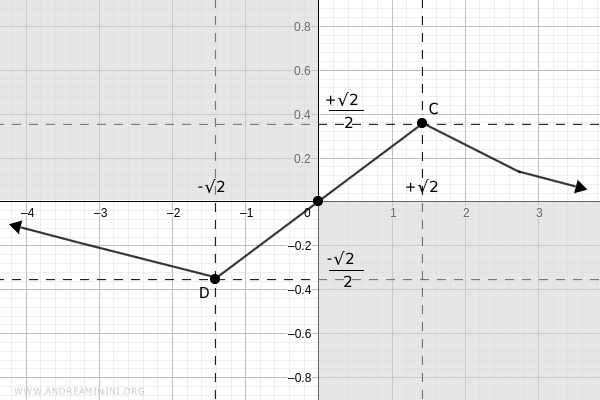
Nel punto x= -√2 si presenta un minimo locale e nel punto x= √2 un massimo locale.
$$ C \ : \ (x,y) = (√2, \frac{√2}{(√2)^2+2}) = (√2, \frac{√2}{4}) $$
$$ D \ : \ (x,y) = (-√2, \frac{-√2}{(-√2)^2+2}) = (-√2, -\frac{√2}{4}) $$
Questo mi permette di perfezionare la costruzione del grafico.
Concavità e convessità
Calcolo la derivata seconda della funzione per trovare gli intervalli in cui la funzione è concava o convessa.
$$ f'(x) = D'[\frac{-x^2+2}{(x^2+2)^2}] = $$
$$ = \frac{-2x(x^2+2)^2-2(x^2+2)(-x^2+2)2x}{(x^2+2)^4} $$
$$ = \frac{-2x(x^2+2)-2(-x^2+2)2x}{(x^2+2)^3} $$
$$ = \frac{-2x(x^2+2)-4x(-x^2+2)}{(x^2+2)^3} $$
$$ = \frac{-2x^3-4x+4x^3-8x}{(x^2+2)^3} $$
$$ = \frac{2x^3-12x}{(x^2+2)^3} $$
$$ = \frac{2x(x^2-6)}{(x^2+2)^3} $$
Studio il segno della derivata seconda.
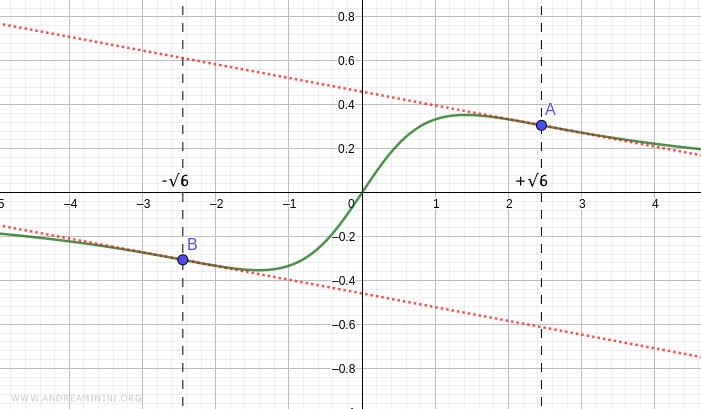
La funzione è concava nell'intervallo (-∞,-√6) e nell'intervallo (0,√6)
E' convessa negli intervalli (-√6,0) e (√6,∞).

Dal punto di vista grafico la funzione è la seguente
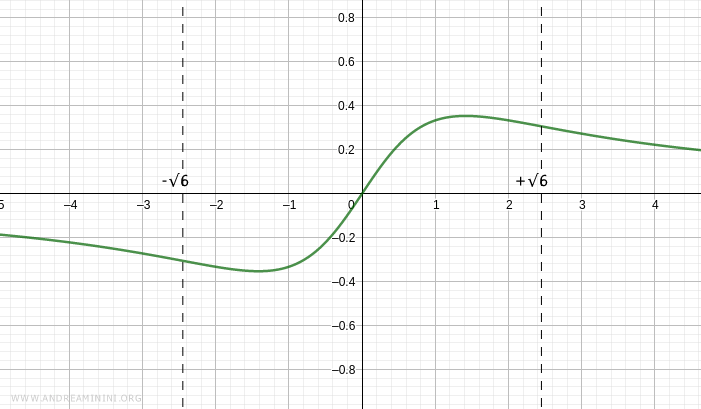
Nei punti x=-√6 e x=√6 ci sono due punti di flesso discendenti.
$$ A \ : \ (x,y) = (√6, \frac{√6}{(√6)^2+2}) = (√6, \frac{√6}{8}) $$
$$ B \ : \ (x,y) = (-√6, \frac{-√6}{(-√6)^2+2}) = (-√6, -\frac{√6}{8}) $$
Dal punto di vista grafico
E così via.
