Esercizio studio della funzione 3
In questo esercizio studio la funzione
$$ f(x)=\frac{x^2+2}{x} $$
Dominio
La funzione è definita in tutto l'insieme dei numeri reali tranne nel punto x=0, dove si annulla il denominatore della frazione.
$$ D_f = (-\infty, 0) \cup (0, \infty) $$
Punti indefiniti
Il punto x=0 è un punto indefinito dove potrebbe esserci un asintoto verticale.
Calcolo il limite destro e sinistro.
$$ \lim_{x \rightarrow 0^+} \frac{x^2+2}{x} = + \infty $$
$$ \lim_{x \rightarrow 0^-} \frac{x^2+2}{x} = - \infty $$
Nel intorno x=0 la funzione tende a +∞ a destra e a -∞ a sinistra.
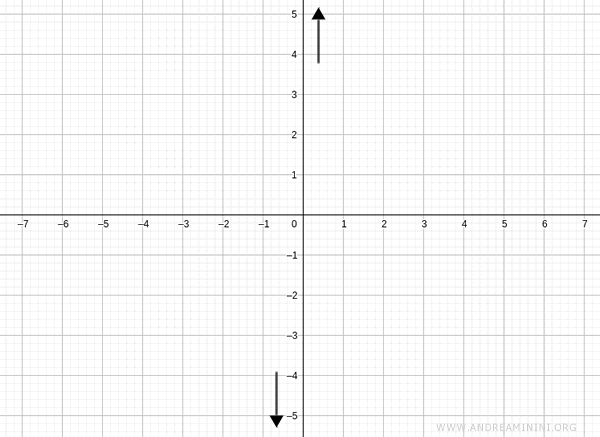
Asintoti orizzontali
Ora studio il comportamento asintotico della funzione per x→+∞ e x→-∞
$$ \lim_{x \rightarrow + \infty} \frac{x^2+2}{x} = + \infty $$
$$ \lim_{x \rightarrow - \infty} \frac{x^2+2}{x} = - \infty $$
La funzione tende a +∞ per x→+∞ e a -∞ per x→-∞.
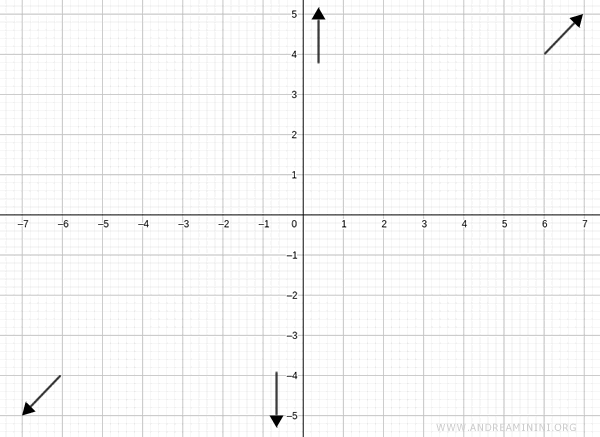
Le intercette con gli assi
Per x=0 la funzione ha un punto indefinito.
$$ f(0) = \frac{0^2+2}{0} $$
L'intercetta con l'asse verticale si verifica in y=0
$$ \frac{x^2+2}{x} = 0 $$
Moltiplico per x entrambi i membri
$$ \frac{x^2+2}{x} \cdot x = 0 \cdot x $$
$$ x^2 +2 = 0 $$
$$ x^2 = -2 $$
L'equazione di 2° grado non ha soluzioni reali.
Quindi, la funzione non interseca l'asse delle ordinate y.
Lo studio del segno
La funzione è negativa nell'intervallo (-∞,0) e positiva nell'intervallo (0,∞).
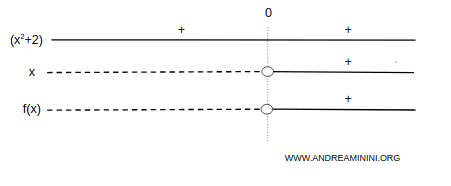
Questo mi permette di eliminare alcune aree del piano cartesiano in cui la funzione non passa (aree in grigio).
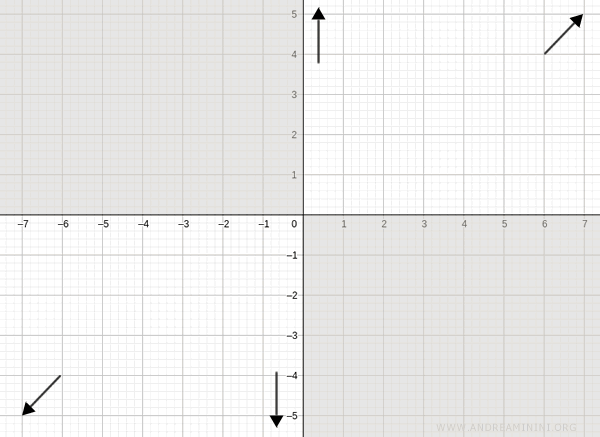
Crescenza e decrescenza
Calcolo la derivata prima della funzione per studiare la crescenza e la decrescenza della funzione.
$$ f'(x) = D[ \frac{x^2+2}{x} ] = \frac{2x \cdot x - (x^2+2) }{x^2} = \frac{2x^2-x^2-2}{x^2} = \frac{x^2-2}{x^2} $$
Studio il segno della derivata prima
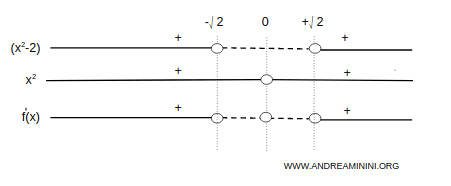
La funzione è crescente nell'intervallo (-∞,-√2) e (√2,∞).
E' decrescente nell'intervallo (-√2,√2)
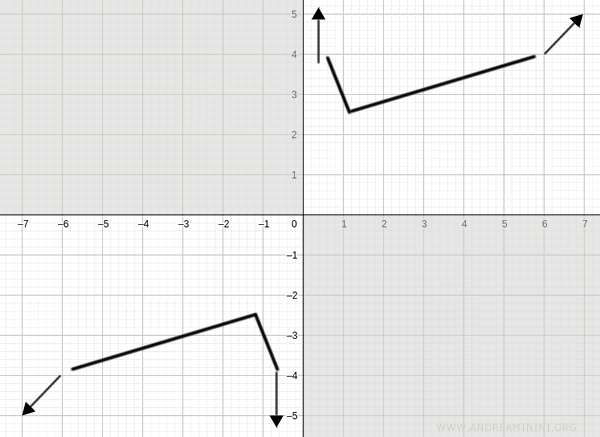
Nel punto x=-√2 si presenta un massimo locale, perché in x=-√2 la derivata prima è nulla f'(x)=0 e nell'intorno di x=-√2 la derivata prima crescente a sinistra e decrescente a destra.
Il punto di massimo locale è
$$ (-2, f(-\sqrt{2})) = (-2, \frac{x^2+2}{x}) = (-2, \frac{(-\sqrt{2})^2+2}{-\sqrt{2}}) = (-2,-\frac{4}{\sqrt{2}}) $$
Nel punto x=2 si presenta un minimo locale, perché in x=√2 la derivata prima è nulla f'(x)=0 e nell'intorno di x=2 la derivata prima decrescente a sinistra e crescente a destra.
Il punto di minimo locale è
$$ (2, f(\sqrt{2})) = (2, \frac{x^2+2}{x}) = (2, \frac{(\sqrt{2})^2+2}{\sqrt{2}}) = (2,\frac{4}{\sqrt{2}}) $$
Concavità e convessità
Calcolo la derivata seconda della funzione per studiare i tratti in cui è concava o convessa.
$$ f''(x) = D'[\frac{x^2-2}{x^2}] = $$
$$ = \frac{2x(x^2)-(x^2-2)(2x)}{x^4} $$
$$ = \frac{2x^3-2x^3+4x}{x^4} $$
$$ = \frac{4x}{x^4} $$
$$ = \frac{4}{x^3} $$
La funzione è concava nell'intervallo (-∞, 0) e convessa nell'intervallo (0,∞).
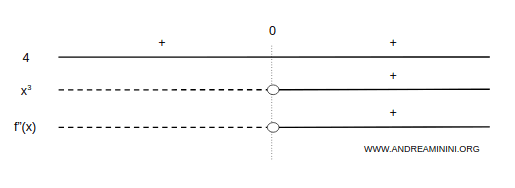
Il grafico della funzione assume questo aspetto.
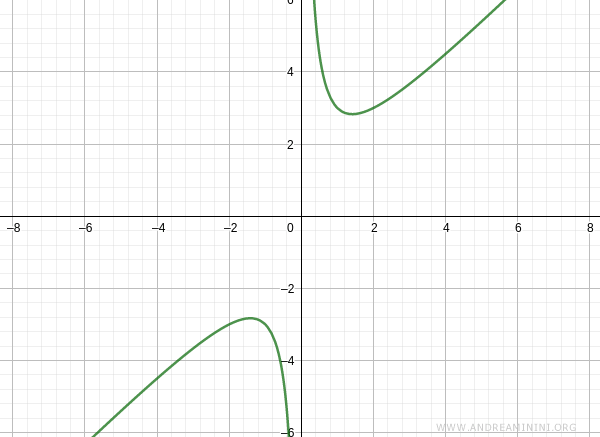
Asintoto obliquo
Verifico la presenza di un eventuale asintoto obliquo.
$$ m = \lim_{x \rightarrow +\infty} \frac{f(x)}{x} = \lim_{x \rightarrow +\infty} \frac{\frac{x^2+2}{x}}{x} = \lim_{x \rightarrow +\infty} \frac{x^2+2}{x^2} = 1 $$
Il coefficiente angolare m è diverso da ∞ quindi posso calcolare q
$$ q = \lim_{x \rightarrow +\infty} f(x)-mx = \lim_{x \rightarrow +\infty} \frac{x^2+2}{x}-x = \lim_{x \rightarrow +\infty} \frac{2}{x} = 0 $$
Entrambi i limiti sono finiti, quindi c'è un asintoto obliquo per x→∞
L'equazione della retta è mx+q ossia x
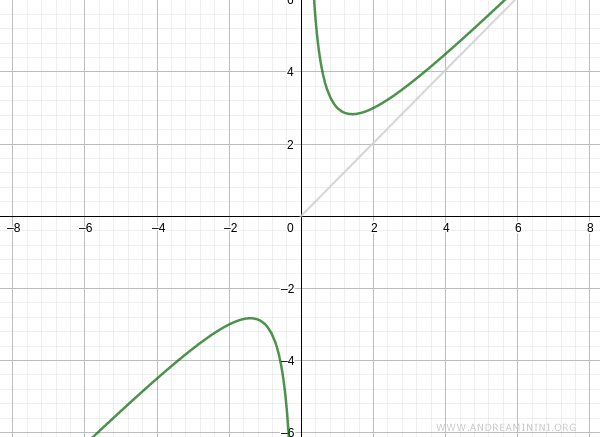
Ora verifico l'asintoto obliquo per x→-∞
$$ m = \lim_{x \rightarrow -\infty} \frac{f(x)}{x} = \lim_{x \rightarrow +\infty} \frac{\frac{x^2+2}{x}}{x} = \lim_{x \rightarrow +\infty} \frac{x^2+2}{x^2} = 1 $$
Il coefficiente angolare m è diverso da ∞ quindi posso calcolare q
$$ q = \lim_{x \rightarrow -\infty} f(x)-mx = \lim_{x \rightarrow +\infty} \frac{x^2+2}{x}-x = \lim_{x \rightarrow +\infty} \frac{2}{x} = 0 $$
Entrambi i limiti sono finiti, quindi c'è un asintoto obliquo per x→-∞
L'equazione della retta è mx+q ossia x
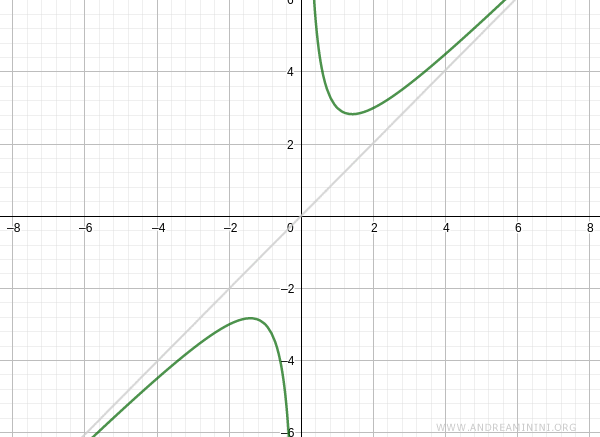
E così via.
