Algebre di Boole
Un algebra di Boole è un reticolo limitato distributivo con almeno due elementi distinti (0,1), un insieme non vuoto B, due operazioni binarie addizione (+) e moltiplicazione (·) e un'operazione unaria - detta complemento $$ ( B,+,\cdot,\overline{ },0,1) $$ che soddisfano le seguenti proprietà:
- Comportamento 0 e 1 $$ a+0=a \\ a \cdot 0 = 0 \\ a+1=1 \\ a \cdot 1 = a $$
- Proprietà commutative $$ a+b=b+a \\ a \cdot b = b \cdot a $$
- Proprietà associative $$ (a+b) +c = a+(b+c) \\ ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) $$
- Proprietà di assorbimento $$ a \cdot (a+b) = a \\ a + (a \cdot b ) = a $$
- Proprietà distributive $$ a \cdot (b+c) = ( a \cdot b ) + (a \cdot c ) \\ a+(b \cdot c) = (a+b) \cdot (a+c) $$
- Proprietà del complemento $$ \overline{\overline{a}}=a \\ \overline{a+b} = \overline{a} \cdot \overline{b} \\ a \cdot \overline{a} = 0$$
Nota. La più semplice algebra di Boole è ovviamente l'algebra booleana (B,and,or,not,0,1). Tuttavia ce ne sono molte altre.
Esempio
L'insieme delle parti P(S) e un insieme finito composto da n elementi.
Ad esempio, n=3 elementi.
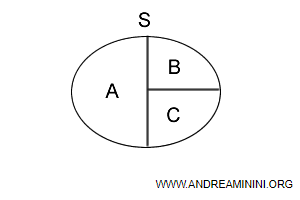
Nota. Nell'insieme delle parti P(S) non ci sono intersezioni tra gli elementi. L'unione degli elementi è uguale all'insieme S.
L'elemento 0 (minimo) del reticolo è l'insieme vuoto ø.
L'elemento 1 (massimo) del reticolo è l'insieme S.
Aggiungo tre operazioni della teoria degli insiemi
- Unione di insiemi ∪ (or)
- Intersezione tra insiemi ⋂ (and)
- Differenza tra insiemi (/)
Nota. L'unione, l'intersezione e la differenza della teoria degli insiemi sono operazioni equivalenti alla somma logica (+), il prodotto logico (·) e il complemento logico (-).
Ho così ottenuto una algebra di Boole.
$$ ( P(S), \cap, \cup, /, ø , S) $$
Prendo tre elementi A, B, C appartenenti all'insieme P(S) e verifico se tutte le proprietà sono soddisfatte.
Comportamento 0 e 1
$$ A \cup Ø=A \\ A \cap Ø = Ø \\ A \cup S=S \\ A \cap S = A $$
Commutativa
$$ A \cup B=B \cup A \\ A \cap B = B \cap A $$
Associativa
$$ (A \cap B) \cap C = A \cap (B \cap C) \\ ( A \cup B ) \cup C = A \cup ( B \cup C ) $$
Assorbimento
$$ A \cap (A \cup B) = A \\ A \cup (A \cap B ) = A $$
Distributiva
$$ A \cap (B \cup C) = ( A \cap B ) \cup (A \cap C ) \\ A \cup (B \cap C) = (A \cap B) \cup (A \cap C) $$
Complemento
$$ S/(S/A)=A \\ S/(A \cup B) = (S/A) \cap (S/B) \\ A \cap (S/A) = ø $$
Tutte le proprietà sono soddisfatte.
E' un'algebra di Boole.
Come riconoscere un algebra di Boole
Un'algebra di Boole è un reticolo algebrico.
Quindi, è un insieme parzialmente ordinabile secondo una particolare relazione.
Per capire se un reticolo è un algebra di Boole, devo verificare se soddisfa tutte le caratteristiche.
Esempio
Definisco l'insieme dei numeri positivi interi divisori di 20.
$$ ( B, | ) = \{ 1, 2, 5, 10 \} $$
Poi definisco due operazioni binarie:
- inf ( ∧ ) = massimo comune divisore MCD(x,y)
- sup ( ∨ ) = minimo comune multiplo mcm(x,y)
Quindi l'insieme diventa
$$ ( B, | , ∨ , ∧ ) $$
L'insieme è un reticolo
| inf | sup | |
|---|---|---|
| ( 1 , 2 ) | 1 | 2 |
| ( 1 , 5 ) | 1 | 5 |
| ( 1 , 10 ) | 1 | 10 |
| ( 2 , 5 ) | 1 | 10 |
| ( 2 , 10 ) | 2 | 10 |
| ( 5 , 10 ) | 5 | 10 |
E' un reticolo limitato perché ammette un minimo (1) e un massimo (10).
Ecco il diagramma di Hasse.
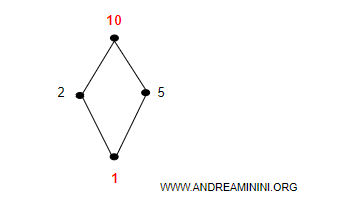
E' anche un reticolo distributivo perché soddisfa la legge distributiva per ciascuna coppia di elementi.
$$ a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)$$
$$ a ∨(b ∧ c) = (a ∨ b) ∧ (a ∨ c) $$
Nota. Posso anche scriverla in questa forma $$ inf ( a, sup(a,c) ) = sup ( inf(a,b) , inf(a, c) ) $$ $$ sup ( a, inf(a,c) ) = inf ( sup(a,b) , sup(a, c) ) $$
Faccio una rapida verifica prendendo tre elementi a=1, b=2, c=5
Prima proprietà
$$ a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)$$
$$1 ∧ (2 ∨ 5) = (1 ∧ 2) ∨ (1 ∧ 5)$$
$$1 ∧ (1) = (1) ∨ (1) $$
$$1 = 1 $$
Seconda proprietà
$$ a ∨(b ∧ c) = (a ∨ b) ∧ (a ∨ c) $$
$$ 1 ∨(2 ∧ 5) = (1 ∨ 2) ∧ (1 ∨ 5) $$
$$ 1 ∨(1) = (2) ∧ (5) $$
$$ 1 = 1 $$
Entrambe le proprietà distributive sono soddisfatte.
Ora sostituisco il massimo con il simbolo 1 e il minimo con 0.
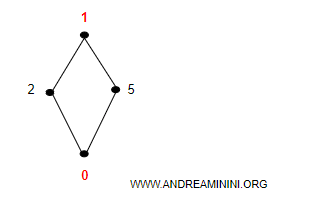
Quindi l'insieme diventa
$$ ( B, | , ∨ , ∧ , 0 , 1 ) $$
Poi verifico se il reticolo è con complemento.
$$ \forall a \in B \rightarrow a ∧ b = 0 , a ∨ b = 1 $$
Escludendo gli estremi devo verificare soltanto la coppia (2,5)
$$ 2 ∧ 5 = 0 $$
$$ 2 ∨ 5 = 1 $$
Quindi, il complemento di 2 è 5 e il complemento di 5 è 2.
Tutti gli elementi hanno almeno un complemento.
E' un insieme con complemento C.
$$ ( B, | , ∨ , ∧ , C, 0 , 1 ) $$
A questo punto, posso verificare se l'insieme risponde a tutte le proprietà delle algebre di Boole.
Per semplicità svolgo la verifica soltanto sulla legge di assorbimento.
$$ a \cdot (a+b) = a \\ a + (a \cdot b ) = a $$
Presa la coppia (2,5)
$$ \begin{cases} 2 \cdot (2+5) = 2 \\ 2 + (2 \cdot 5 ) = 2 \end{cases} $$
Nota. Nella logica equivale a scrivere $$ \begin{cases} 2 ∧ (2 ∨ 5) = 2 \\ 2 ∨ (2∧ 5 ) = 2 \end{cases} $$
$$ \begin{cases} 2 \cdot (1) = 2 \\ 2 + (0 ) = 2 \end{cases} $$
$$ \begin{cases} 2 = 2 \\ 2 = 2 \end{cases} $$
La legge di assorbimento è soddisfatta.
Allo stesso modo posso verificare tutte le altre leggi.
Il reticolo è un'algebra di Boole.
