Isomorfismo algebre di Boole
Date due algebre di Boole B e B' un isomorfismo è una corrispondenza biunivoca φ tra (B.+,-) e (B',+',-') tale che per ogni x,y di B $$ φ(x+y) = φ(x)+'φ(y) \\ φ(x \cdot y) = φ(x) \cdot' φ(y) \\ φ( \overline{x} ) = \overline{φ(x)} ' $$
Esempio di isomorfismo
Questo diagramma di Hasse mostra l'algebra di Boole dei divisori di 60.
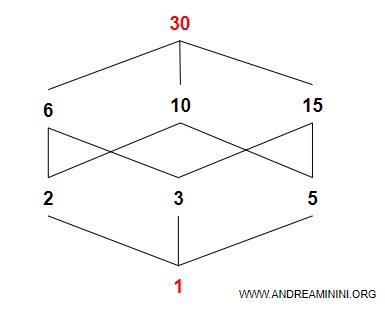
Gli atomi dell'algebra sono gli elementi 2,3,5.
Un isomorfismo di questa struttura è l'algebra delle parti P(x) con tre elementi (a,b,c).
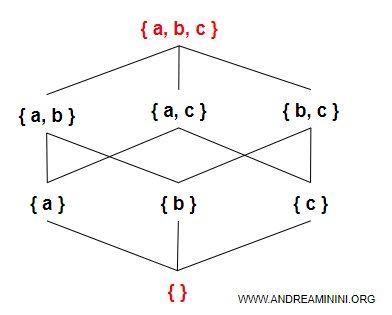
La struttura è sempre la stessa.
Sono due isomorfismi tra algebre di Boole.
Entrambe le algebre hanno lo stesso numero di atomi (2,3,5) e (a,b,c) ossia tre atomi.
Questo preannuncia un teorema molto importante.
Dato un numero n di atomi esiste una e una sola algebra di Boole con cardinalità 2n.
Inoltre, posso affermare che
Dato un'algebra di Boole con n atomi esiste sempre un isomorfismo con l'insieme delle parti P(x) con n elementi.
In conclusione, se due algebre di Boole hanno lo stesso numero di atomi allora sono anche isomorfe.
Il teorema di rappresentanza
Ogni algebra di Boole con un numero finito di atomi è isomorfa all'insieme delle parti P(x).
Dimostrazione
Se B è un'algebra di Boole con n atomi
$$ x_1,x_2,..., x_n $$
Allora l'insieme degli indici degli atomi è
$$ X = \{ 1, 2, ... , n \} $$
Ogni elemento dell'algebra di Boole può essere scritta in modo unico come somma di atomi.
$$ x = x_3+x_4+x_6 $$
Quindi, a ogni elemento dell'algebra di Boole è associata una n-pla composta da indici.
$$ f(x) = \{ 3, 4, 6 \} $$
Pertanto, esiste una corrispondenza biunivoca tra ogni elemento x dell'algebra di Boole con le n-ple dell'insieme delle parti P(X).
$$ f(x) = \{ i | 1 \le i \le n ∧ δ_i = 1 \} $$
Un esempio pratico
Questa algebra di Boole (B,I) è ordinata per divisibilità ed è composta da n=3 atomi e 23=8 elementi.

Gli atomi dell'algebra di Boole sono 2, 3, 5.
$$ x_1 = 2 \\ x_2 = 3 \\ x_3 = 5 $$
Pertanto, l'insieme X è composto dagli indici i=1,...,3 con n=3
$$ X = \{ 1, 2, 3 \} $$
Ogni numero dell'algebra di Boole può essere scritto come somma di atomi x1=2, x2=3, x3=5
| x | somma di atomi | P(X) |
|---|---|---|
| 30 | x1∨x2∨x3 | {1,2,3} |
| 15 | x2∨x3 | {2,3} |
| 10 | x1∨x3 | {1,3} |
| 6 | x1∨x2 | {1,2} |
| 5 | x3 | {3} |
| 3 | x2 | {2} |
| 2 | x1 | {1} |
| 1 | Ø |
Tra l'algebra di Boole (B,|) e l'algebra di Boole (P(x), ⊆) c'è un isomorfismo.
Si tratta di una corrispondenza biunivoca. A ogni elemento della prima algebra corrisponde uno e un solo elemento della seconda, e viceversa.
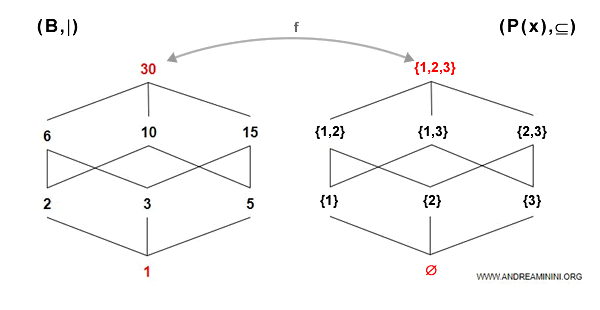
Verifico se soddisfa le regole degli isomorfismi prendendo due elementi x=15 e y=6 di (B,I)
$$ f(15+6) = f(15∨6) = f(30) = \{ 1,2,3 \} $$
$$ f(15)+f(6) = \{ 2,3 \} ∪ \{ 2,3 \} = \{ 1,2,3 \} $$
La prima condizione è soddisfatta.
Verifico la seconda condizione.
$$ f(15·6) = f(15∧6) = f(3) = \{ 2 \} $$
$$ f(15)·f(6) = \{ 2,3 \} ⋂ \{ 1,2 \} = \{ 2 \} $$
La seconda condizione è soddisfatta.
Verifico la terza condizione.
$$ f(\bar{15}) = f(2) = \{1 \} $$
$$ \bar{f(15)} = \bar{ \{ 2,3 \} } = \{1 \} $$
Anche l'ultima condizione è soddisfatta.
Nota. Quest'ultima operazione in (P(x),⊆) è l'insieme complemento.
E così via.
