Reticolo con complemento
Un reticolo limitato L si dice reticolo con complemento se per ogni elemento a di L esiste almeno un elemento b di L tale che $$ a ∧ b = 0 $$ $$ a ∨ b = 1 $$
I simboli 0 e 1 indicano rispettivamente il minimo e il massimo del reticolo.
Un reticolo si dice complementato se per ogni suo elemento esiste almeno un complemento.
Nota. Ogni elemento può ammettere zero, uno o anche più di un complemento.
Come verificare se un reticolo è complementato
Il procedimento per capire se un reticolo è complementato
- Verifico se è il reticolo è limitato. Se non è limitato, il procedimento termina qui, perché un reticolo non limitato non può essere complementato.
- Controllo se ogni elemento del reticolo limitato ha un complemento. Dal confronto escludo il massimo (1) e il minimo (0) del reticolo. Escludo anche i confronti diretti tra gli elementi del reticolo perché gli estremi non potrebbero mai essere uguali al massimo e al minimo.
Se ogni elemento del reticolo ha almeno un complemento, allora il reticolo è complementato.
Esempi pratici
Esempio 1
Ho il seguente reticolo composto da 5 elementi.
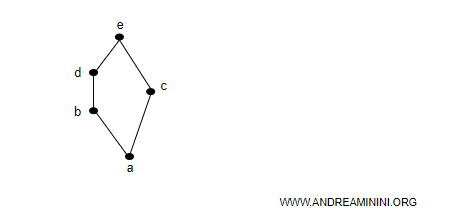
E' un reticolo limitato perché ha il massimo e il minimo.
Sostituisco il massimo e il minimo con i simboli 1 e 0.
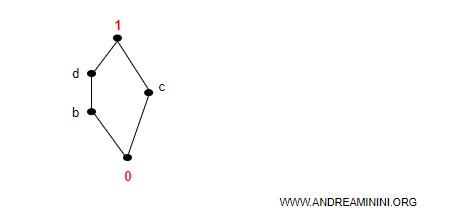
Poi controllo le coppie formate da ciascun elemento con gli altri, escludendo dal confronto il massimo e il minimo del reticolo.
- Il complemento di b è l'elemento c
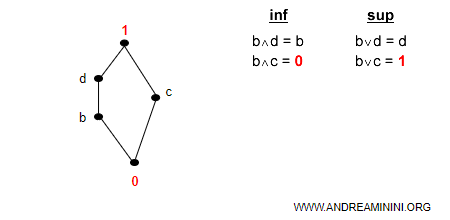
Nota. Per completezza nell'esempio calcolo anche i confronti diretti come (b,d). Lo faccio soltanto per spiegare meglio il procedimento. Tuttavia, è del tutto inutile farlo. Qualsiasi confronto diretto è diverso dal massimo o il minimo.
- Il complemento di c sono gli elementi b e d
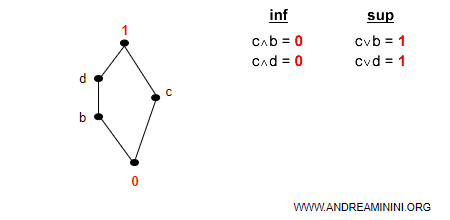
Nota. Questo caso dimostra che un elemento del reticolo può avere anche più complementi. Soltanto nei reticoli distributivi un elemento può avere eventualmente un solo complemento. Per continuare i confronti me ne basta uno solo.
- Il complemento di d è l'elemento c
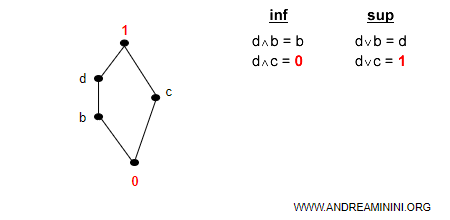
Tutti gli elementi del reticolo hanno un complemento.
Pertanto, si tratta di un reticolo complementato.
Esempio 2
Ho un reticolo L con 7 elementi.
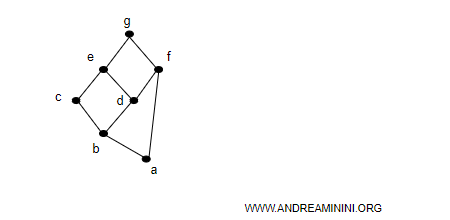
Il reticolo ha un minimo e un massimo, quindi è limitato e posso procedere.
Sostituisco il minimo e il massimo con 0 e 1.
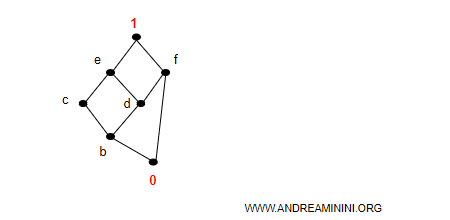
Formo le coppie tra ciascun elemento e gli altri.
(b,c) (b,d) (b,e) (b,f)
(c,b) (c,d) (c,e) (c,f)
(d,b) (d,c) (d,e) (d,f)
(e,b) (e,c) (e,d) (e,f)
(f,b) (f,c) (f,d) (f,e)
Poi verifico se ogni elemento ha un complemento.
Nota. I confronti diretti come (b,c) , (b,d) , (c,e), (d,e) posso anche eliminarli. E' evidente che questi non possano essere uguali al massimo o al minimo del reticolo. In questo esempio li scrivo soltanto per dimostrare e spiegare meglio il procedimento. In realtà, soltanto i confronti indiretti sono importanti (b,f) , (c,d) , (e,f) , (b,e).
- L'elemento d non ha un complemento
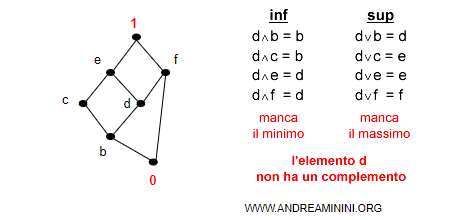
Nota. L'intersezione dell'elemento d con gli altri elementi non è mai uguale al minimo (0) del reticolo. Già questo sarebbe sufficiente per affermare che l'elemento d non ha complemento. In questo caso non si verifica nemmeno l'altra condizione. L'unione dell'elemento d con gli altri elementi non è mai uguale al massimo (1) del reticolo.
Non occorre proseguire oltre.
Il reticolo non è complementato perché l'elemento d non ha un complemento.
Esempio 3
L'insieme delle parti (P(S), inc) è un reticolo limitato
$$ \min (P(S))=ø $$ $$ \max (P(S))=S $$
E' anche un reticolo complementato?
Prendo un generico elemento x di P(S).
L'elemento x ha un complemento se esiste un elemento y di P(S) tale che
$$ ( x ∨ y = S ) ∧ ( x ∧ y = ø ) $$
Sostituisco le unioni e intersezioni logiche con quelle dell'insiemistica.
$$ ( x ∪ y = S ) ∧ ( x ⋂ y = ø ) $$
Questo elemento esiste, è la differenza S/x
$$ ( x ∪ S/x = S ) ∧ ( x ⋂ S/x = ø ) $$
Entrambe le espressioni sono vere.
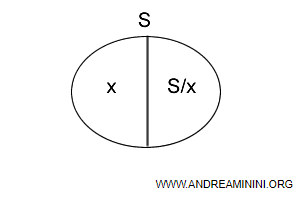
L'insieme delle parti è un reticolo complementato.
Reticoli distributivi e complementati
In un reticolo distributivo il complemento di un elemento del reticolo se esiste è unico.
I reticoli distributivi e complementati sono detti reticoli booleani.
E così via.
