Entropia
L'entropia misura il grado di disordine di un sistema. E' una delle funzioni di stato di un sistema termodinamico. E' generalmente indicata con il simbolo S. $$ S = K \cdot \ln W $$ detto principio di Boltzmann.
Dove K è la costante di Boltzmann e W è la probabilità termodinamica di uno stato del sistema di verificarsi.
- Se l'entropia è bassa il sistema è ordinato e l'energia è massima.
- Se l'entropia è alta il sistema è disordinato e l'energia è minima.
Quindi, l'entropia può essere vista anche come la quantità di energia disponibile all'interno di un sistema chiuso.
Nota. L'entropia è anche conosciuta come seconda legge della termodinamica. In natura tutto tende spontaneamente da uno stato di bassa entropia (max. energia) a uno stato di alta entropia (min. energia). Quindi, ogni sistema tende spontaneamente dall'ordine al disordine.
Cos'è l'entropia
Secondo l'entropia, un sistema isolato si trasforma ed evolve nel tempo fino a raggiungere uno stato di equilibrio finale macroscopico in cui le differenze locali sono minime.
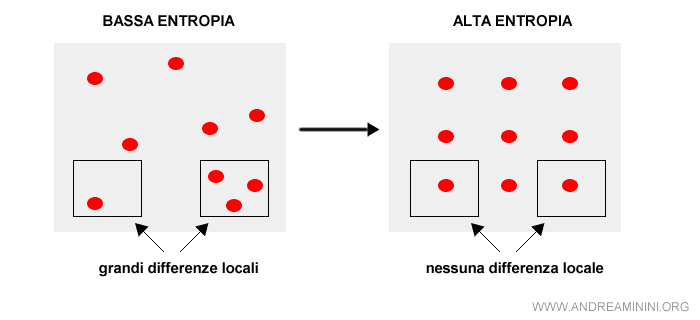
Si passa così da una situazione iniziale di ordine a una finale di disordine perché è molto più difficile sapere dove si concentrano le risorse.
Da una situazione di bassa entropia ( max energia ) a una di alta entropia ( minima energia disponibile ).
La trasformazione è irreversibile.
La morte termica. La situazione finale ad alta entropia è anche detta "morte termica" perché il sistema si trova in uno stato perenne di quiete, equilibrio e pace. Non c'è più alcuna energia o spinta al cambiamento. L'equilibrio è perfetto ma il sistema è morto.
Come si misura l'entropia
In genere l'entropia è indicata con il simbolo S.
Nel sistema internazionale viene misurata con il rapporto J/K tra la quantità di calore scambiato ( misurato in Joule ) e la temperatura in cui avviene lo scambio ( misurata in gradi Kelvin ).
Un esempio pratico di entropia
Un semplice esempio può aiutare a capire meglio il concetto. Supponiamo di avere due bombole ( sistemi chiusi ). La prima è piena di gas, la seconda è vuota. Entrambe sono chiuse.
Inizialmente questi due sistemi sono isolati e si trovano in un equilibrio in stato di quiete e di ordine.
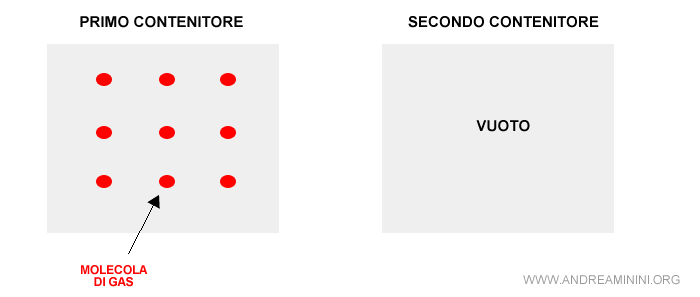
Nota. Il sistema è in quiete perché non c'è nessuna spinta spontanea al cambiamento. E' in ordine perché, grazie alle differenze locali, è più facile capire dove si trovano le molecole del gas ...sono nel primo contenitore. Quindi, è inutile cercarle anche nel secondo contenitore.
Se colleghiamo le due bombole tra loro, lo stato di quiete e di ordine viene interrotto.
Ora le due bombole sono diventate un unico sistema chiuso in cui prevale il disordine. Una zona è sotto pressione, l'altra è vuota.
Pertanto, le molecole del gas si spostano dal primo al secondo contenitore fino a occupare tutto il volume disponibile.
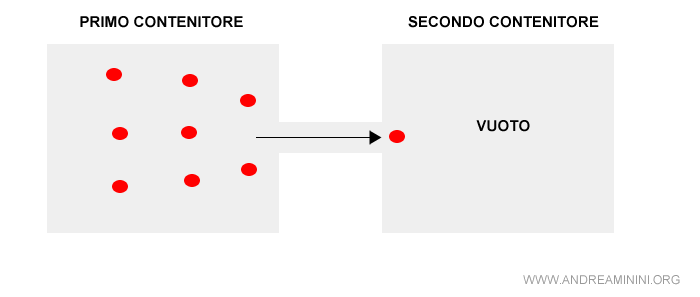
Dallo stato di quiete si passa a uno stato dinamico che cambia continuamente.
Nota. In questo stadio iniziale l'entropia è minima perché il sistema è caratterizzato da notevoli differenze locali. Una parte del sistema è completamente diversa dall'altra. Le molecole si spostano da una parte all'altra sprigionando una grande quantità di energia.
Questo processo dinamico non è però infinito. E' comunque destinato a finire.
Quando le molecole sono equamente distribuite in tutto lo spazio, cessano di muoversi e si raggiunge un equilibrio finale statico.
Il sistema torna in uno stato di quiete in cui però prevale il disordine perché è più difficile sapere dove si trovano le molecole del gas.
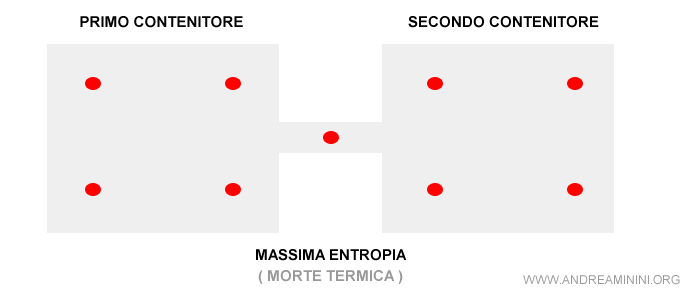
Nello stadio finale non ci sono più differenze locali. Cessa ogni dinamica e si instaura un equilibrio perfetto.
La quantità di molecole per centimetro cubo è ovunque la stessa e le molecole non si spostano più. Pertanto, il sistema non rilascia più energia.
In conclusione, il sistema ha raggiunto l'entropia massima.
Il sistema è così passato da una situazione a bassa entropia ( max. energia ) a un'altra situazione ad alta entropia ( min. energia disponibile ).
Nota. Lo stesso fenomeno si verifica in qualsiasi sistema chiuso. Anche l'Universo è un sistema chiuso, per quanto sia grande, e risponde alle stesse leggi dell'entropia. Non a caso la morte termica è uno dei possibili scenari futuri dell'Universo in astrofisica. Anche il cosmo nasce ( Big Bang ) ed è destinato a morire ( Big Freeze ).
Il processo entropico è irreversibile
Una delle caratteristiche dell'entropia è l'irreversibilità delle trasformazioni.
Una volta raggiunto un equilibrio ad alta entropia, è impossibile tornare all'equilibrio iniziale.
Esempio. Se bruciamo due ciocchi di legno in un camino, il fuoco trasforma la legna in energia e scorie. La reazione chimica trasforma irreversibilmente la materia. Una parte delle molecole si deposita sotto forma di cenere, un'altra viene emessa dai fumi, un'altra ancora in calore. Anche se riuscissimo a mantenere il calore e gli atomi in un sistema chiuso, sarebbe impossibile ricomporli tra loro per ricreare il ciocco di legno iniziale.

La storia del termine entropia
Il termine "entropia" venne ideato dal fisico Rudolf Clausius nel 1868 per spiegare la tendenza di un sistema chiuso verso uno stato di equilibrio termico.
Il concetto venne poi ripreso da Sadi Carnot negli anni '20. Carnot era un ufficiale dell'esercito francese. Studiò l'entropia nei sistemi chiusi.
Carnot si accorse che in un sistema chiuso e limitato, senza scambi con l'esterno ( isolato ), si verifica uno spostamento naturale del calore dalle zone più calde a quelle più fredde.
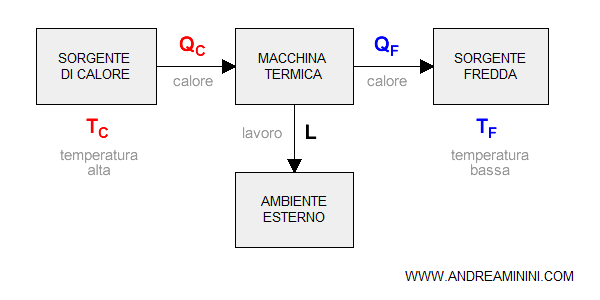
Quando una macchina ( sistema chiuso ) ha un differenziale energetico molto alto, la quantità di energia disponibile è massima. Pertanto, l'entropia è bassa.
La macchina può sprigionare una grande quantità di energia ( forza lavoro ).

La morte termica ( o massima entropia )
Se il differenziale energetico è nullo, la temperatura è costante in ogni parte del sistema chiuso.
In questa circostanza la macchina non può sprigionare energia. Non c'è nessuna spinta al cambiamento.

Questo equilibrio finale è detto "morte termica" o "massima entropia".
La morte termica è un equilibrio perenne.
Il sistema chiuso è destinato a restare in questa situazione per sempre, perché non ha scambio con l'esterno.
Carnot elabora così il paradigma scientifico della termodinamica e le due leggi ( o principi ) della termodinamica.
Quali sono le leggi della termodinamica?
- Prima legge della termodinamica
E' sintetizzabile con il motto "nulla si crea, nulla si distrugge, tutto si trasforma". - Seconda legge della termodinamica
Un sistema chiuso tende spontaneamente e in modo irreversibile verso uno stato di massima entropia nel corso del tempo, ossia una situazione di massimo disordine, priva di differenze locali, in cui l'energia ancora disponibile è minima.
Nota. La prima legge della termodinamica è ottimistica. Ci dà l'illusione che tutto sia eterno. Se la materia si trasforma in energia termica ( calore ), allora l'energia termica può essere recuperata per ricreare la materia. In un ciclo perpetuo ed eterno. Del resto, lo stesso Albert Einstein lega tra loro l'energia e la materia ( E=mc2 ). E' l'ottimismo tipico di inizio Novecento. Purtroppo la realtà è diversa. La seconda legge della termodinamica ci ricorda che la trasformazione è irreversibile. Si passa così a una visione pessimistica o più realistica del futuro.
La formula dell'entropia
L'entropia può essere vista come il numero di stati di un sistema termodinamico. $$ S = K \ln \: W $$
Dove K è la costante di Boltzmann, mentre W è la probabilità termodinamica del sistema di trovarsi in un determinato stato.
Nota. Ogni stato macroscopico dipende a sua volta dalla probabilità di più stati microscopici di verificarsi. Quindi, W può essere considerato come il numero di microstati che definiscono un determinato macrostato.
Esempio
Allo zero assoluto T=0 Kelvin cessano i movimenti termici delle particelle.
Quindi, in un cristallo (sistema) ogni particella occupa una posizione prederterminata senza possibilità di muoversi.
Il sistema può assumere un solo stato (W=1) in una situazione di certezza e ordine perfetti.
In questa circostanza (W=1) l'entropia è zero perché il grado di disordine è nullo.
$$ S = K \ln \: W = K \ln 1 = K \cdot 0 = 0 $$
Man mano che aumenta la temperatura T, le particelle possono muoversi occupando posizioni diverse.
A parità di energia interna, il reticolo cristallino può presentarsi in più stati diversi (W>1).
Pertanto, l'entropia S è maggiore di zero.
$$ S = K \ln \: W > 0 $$
Il grado di disordine del sistema è maggiore.
Nota. Per la stessa ragione l'entropia (S) del ghiaccio è minore rispetto all'entropia dell'acqua (liquida). Nel ghiaccio le molecole H2O sono disposte in modo regolare e possono assumere meno stati rispetto all'acqua liquida. A sua volta l'acqua ha minore entropia rispetto al vapore acqueo.
L'entropia come numero degli stati microscopici del sistema
L'entropia può essere considerata come la misura del numero degli stati microscopici presenti in un sistema.
Lo stato più probabile di un sistema, quello a maggiore entropia, è lo stato macroscopico definito da più stati microscopici.
Esempio
Per capire la differenza tra macrostati e microstati in entropia, spesso si fa l'esempio di due dadi.
Quando lancio due dadi ottengo un punteggio da 2 a 12. Questi sono gli stati macroscopici del sistema (o macrostati).
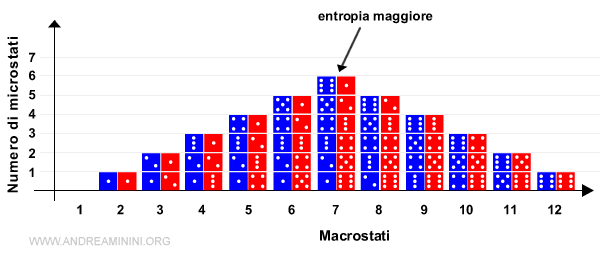
Analizzo gli stati macroscopici 2 e 7 (macrostati)
- Per ottenere il punteggio 2 (stato macroscopico) c'è una sola combinazione possibile (1+1) ossia un solo stato microscopico (o microstato) che definisce il macrostato 2.
- Per ottenere il punteggio 7 (stato macroscopico) ci sono ben sei stati microscopici (1+6,2+5,3+4,4+3,5+2,6+1) che definiscono lo stesso macrostato (7).
Pertanto, lo stato macroscopico 7 è lo stato più probabile del sistema, quello con entropia maggiore (più disordine) e, a sua volta, è anche quello che ha un maggior numero di stati microscopici rispetto agli altri macrostati.
Nota. I macrostati 2 e 12 sono, invece, quelli con entropia minore.
La variazione di entropia
In un sistema termodinamico la variazione di entropia di una trasformazione di stato è determinata dal rapporto $$ \Delta S = \frac{Q_{rev}}{T} $$ Dove Qrev è la quantità di calore Qrev scambiata dal sistema in modo reversibile e T è la temperatura assoluta del sistema.
Pertanto, la variazione di entropia può essere calcolata solo se la trasformazione è reversibile.
Essendo un processo reversibile, posso misurare anche la variazione infinitesimale di entropia considerando costante la temperatura T.
$$ dS = \frac{dQ_{rev}}{T} $$
Nota. In generale una trasformazione è detta reversibile se può essere invertita tramite variazioni infinitesimali in un verso e nel verso opposto.
Dimostrazione
La variabile di stato S misura l'entropia di un sistema termodinamico.
Quando il sistema passa dallo stato 1 allo stato 2 a parità di temperatura (processo isotermo) si registra una variazione di entropia
$$ \Delta S = S_2 - S_1 $$
Poiché il processo è reversibile per definizione, posso calcolare la differenza per variazioni infinitesimali dell'entropia (dS) nell'intervallo da 1 a 2.
$$ \Delta S = S_2 - S_1 = \int_1^2 dS $$
La variazione infinitesimale dell'entropia è pari alla variazione infinitesimale del calore scambiato reversibilmente Qrev in rapporto alla temperatura assoluta T (costante).
$$ \Delta S = \int_1^2 \frac{dQ_{rev}}{T} $$
Poiché la temperatura assoluta T è costante può uscire dall'integrale definito.
$$ \Delta S = \frac{1}{T} \int_1^2 dQ_{rev} $$
L'integrale definito di dQrev nell'intervallo da 1 a 2 è la variabile Qrev che misura la quantità di calore scambiata dal sistema nella trasformazione dallo stato 1 (iniziale) allo stato 2. (finale)
$$ \Delta S = \frac{Q_{rev}}{T} $$
In questo modo ottengo la formula iniziale.
La diseguaglianza di Clausius
La variazione di entropia è sempre maggiore del rapporto tra la quantità del calore scambiata da un processo irreversibile Qrev e la temperatura assoluta T in una trasformazione di stato $$ \Delta S = \frac{Q_{rev}}{T} > \frac{Q_{irrev}}{T} $$
Questo accade perché la quantità di calore scambiata da un processo reversibile Qrev è maggiore di quella di un processo irreversibile Qirrev.
$$ Q_{rev} >Q_{irrev} $$
Quindi, per calcolare la variazione di entropia di una trasformazione di stato occorre trovare un percorso reversibile tra lo stato iniziale e finale.
Il valore assoluto dell'entropia
Il valore assoluto dell'entropia (S) di un sistema a una certa temperatura assoluta T è uguale alla quantità di calore Qrev necessario per scaldare la sostanza da 0 K alla temperatura T tramite un processo reversibile. $$ S = \frac{Q_{rev}}{T} $$
Il terzo principio della termodinamica afferma che l'entropia è nulla S=0 allo zero assoluto (T = 0 K )
$$ S_0 = 0 $$
Pertanto, la variazione di entropia ΔS da zero a una temperatura T>0 qualsiasi è
$$ \Delta S = S_T - S_0 $$
Poiché S0=0 la formula precedente diventa
$$ \Delta S = S_T $$
Quindi, sapendo che
$$ \Delta S = \frac{Q_{rev}}{T} = S_T $$
La variazione di entropia (ΔS) a partire dallo zero assoluto è uguale al valore assoluto dell'entropia alla temperatura assoluta T.
Nota. In questo modo posso calcolare l'entropia a diverse temperature assolute (T>0). Sono particolarmente utili le entropie di trasformazione calcolate nei passaggi di stato di una sostanza.
In una trasformazione a pressione costante il calore scambiato Qrev è uguale alla variazione di entalpia ΔH.
In questi casi posso anche scrivere la formula in questo modo:
$$ \Delta S = \frac{ΔH}{T} = S_T $$
E' sicuramente più semplice da calcolare.
L'entropia molare standard
L'entropia molare standard è la variazione di entropia misurata a pressione costante pari a 1 arm (una atmosfera equivale a circa 1 bar) riscaldando una mole di una sostanza pura alla temperatura T gradi Kelvin a partire dallo zero assoluto (O K) .
Si indica con il simbolo S° e si misura in J/Kmol.
L'entropia molare standard è utile per calcolare la variazione di entropia in una reazione chimica.
Esempio
L'entropia molare standard dell'acqua allo stato liquido H2O(l) è S°=66 J K-1 mol-1
Altri significati di entropia
Il concetto fisico dell'entropia è stato adottato anche nelle scienze sociali con significato più o meno diverso.
- Entropia in economia
In economia l'entropia indica l'irreversibilità dei processi di produzione, i limiti della crescita economica e la scarsità delle materie prime. Se l'entropia è bassa c'è una grande disponibilità di risorse, concentrate e facilmente reperibili a basso costo nel sistema economico. Viceversa, se l'entropia è alta le risorse sono scarse, disperse e in via di esaurimento. - Entropia in comunicazione
Nella teoria della informazione l'entropia indica l'incertezza di un'informazione. Se l'entropia è bassa o nulla, l'informazione contenuta in un messaggio/segnale è certa e un evento è facilmente prevedibile. Viceversa, se l'entropia è alta, l'informazione è molto incerta e un evento è imprevedibile.
E così via.
FAQ
- Domanda
Se l'entropia massima raggiunge l'equilibrio e la quiete perfetta, per quale motivo è uno stato di disordine? Equilibrio e quiete sono sinonimi di ordine non di disordine.
Riposta
L'entropia massima è uno stato di disordine perché è più difficile trovare concentrazioni di risorse. E' uno stato di equilibrio e quiete perché il sistema non ha più alcuna spinta al cambiamento.Esempio. Un recipiente contiene acqua fredda. Verso nel recipiente un bicchiere di acqua calda. Inizialmente nel recipiente è presente una zona di acqua calda e un'altra di acqua fredda ben distinte tra loro. E' una situazione ordinata perché è facile trovare dove si concentra il calore (ordine). Progressivamente il calore si sposta verso le zone fredde e lo spostamento genera energia (enegia massima). Il processo termina quando il recipiente ha la stessa temperatura in ogni parte (equilibrio e quiete). Questa situazione finale è di disordine perché il calore è ormai disperso in ogni parte del recipiente. E' irreversibile perché non torna alla situazione iniziale. E' anche una situazione di bassa energia perché non c'è più alcuna spinta alla trasmissione del calore.
