Vettore velocitÓ
Cos'è il vettore velocità
Il vettore velocità misura la velocità istantanea, la direzione istantanea e il verso di un corpo in movimento nello spazio in un istante temporale.
Il modulo del vettore velocità |v| misura la velocità istantanea del corpo nell'istante t.
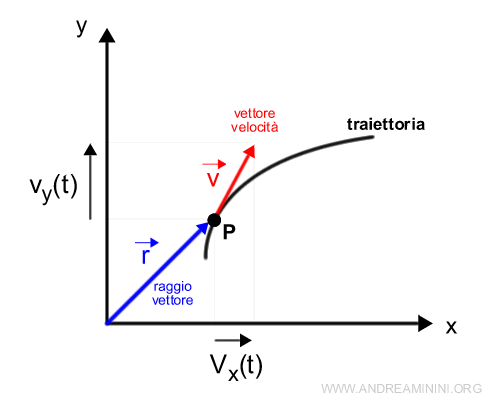
Il vettore velocità è sempre tangente alla traiettoria dello spostamento del corpo nello spazio.
A ogni punto della traiettoria (o istante temporale) è associato un vettore velocità v(t) specifico che descrive il moto del corpo in quel preciso istante.
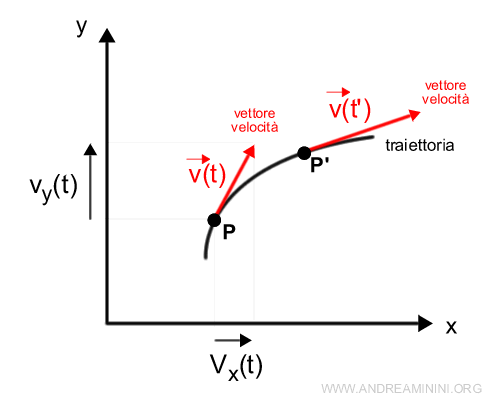
L'insieme dei vettori velocità mi permette di ricostruire il moto del corpo nello spazio e nel tempo.
Come calcolare il vettore velocità
Per ottenere il vettore velocità di un punto P in un istante t, devo derivare il raggio vettore r del punto.
$$ \vec{v}(t) = \frac{d \: \vec{r}(t)}{d \: t } $$
Il modulo del vettore velocità, ossia la lunghezza del vettore, misura la velocità istantanea (grandezza scalare) del corpo nell'istante t.

Posso calcolare il vettore velocità anche a partire dalle velocità componenti.
Scompongo il raggio vettore r nei moti componenti.
$$ \vec{v}(t) = \frac{d \: [x(t)\hat{i} + y(t)\hat{j} + z(t)\hat{k}] }{d \: t } $$
$$ \vec{v}(t) = \frac{d \: x(t)}{d \: t } \hat{i} + \frac{d \: y(t)}{d \: t } \hat{j} + \frac{d \: z(t)}{d \: t } \hat{k} $$
Dove dx(t)/dt = vx, dy(t)/dt = vy e dz(t)/dt = vz,mentre i, j, k sono i versori del sistema di riferimento.
$$ \vec{v}(t) = v_x \cdot \hat{i} + v_y \cdot \hat{j} + v_z \cdot \hat{k} $$
Il modulo del raggio vettore è uguale al quadrato delle componenti della velocità
$$ v = \sqrt{v_x^2 + v_y^2 + v_z^2} $$
Ad esempio, se le componenti velocità sono vx(t)=3 e vy(t)=4 la velocità istantanea del corpo è pari a 5 m/s.
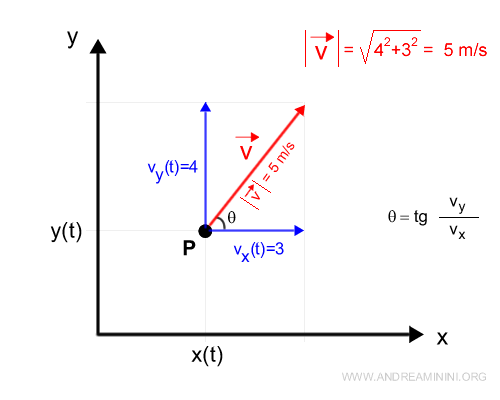
Il rapporto tra le velocità componenti vy/vx è uguale alla tangente dell'angolo θ formato dal vettore velocità rispetto all'asse x.
$$ \tan θ = \frac{v_x}{v_y} $$
E così via.
