La velocitÓ media e istantanea
Nel moto rettilineo di un punto materiale posso misurare due tipi di velocità: la velocità media e la velocità istantanea.
La velocità media
A] La velocità media in una retta
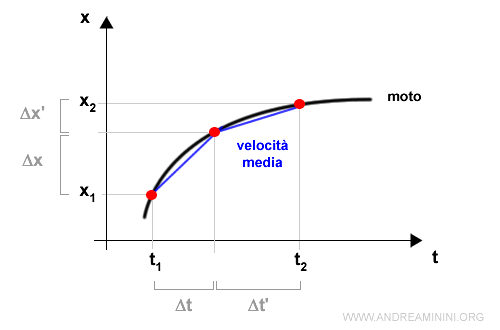
Per calcolare la velocità media rilevo la posizione x della particella in un istante iniziale t1 e finale t2.
$$ x_1 = x(t_1) \\ x_2 = x(t_2) $$
La differenza x2-x1 indica lo spazio percorso S.
La differenza t2-t1, invece, indica il tempo trascorso T.
Essendo un moto rettilineo il punto si muove lungo una linea nel corso del tempo.
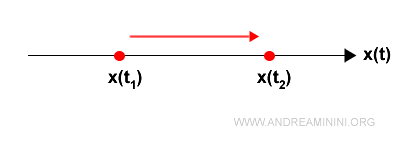
Nota. Il segno della differenza x2-x1 fornisce l'informazione sul verso del moto. Se l'incremento Δx>0 allora il punto si sposta da sinistra verso destra. Viceversa, se Δx<0 da destra verso sinistra. Se Δx=0 il punto è fermo in stato di quiete.
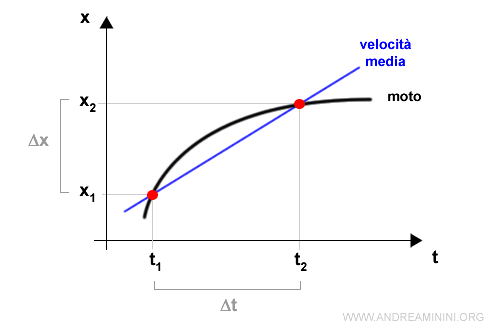
Per studiare la velocità del punto è preferibile rappresentare la relazione tra lo spazio e il tempo sul diagramma cartesiano.
Sapendo che la velocità è il rapporto tra spazio e tempo.
$$ V = \frac{S}{T} = \frac{Δx}{Δt} = \frac{x_2-x_1}{t_2-t_1} $$
La velocità media ( tratto blu ) è un'informazione complessiva sul moto rettilineo della particella.
Tuttavia, non mi dice nulla sulla dinamica effettiva del moto.
Esempio. Nel esempio precedente il punto decelera nel tempo. La curva del moto (nera) è quasi verticale nella posizione iniziale x1 (velocità elevata) e quasi orizzontale nella posizione finale x2 (velocità bassa). E' impossibile accorgersi di questa caratteristica osservando la velocità media (blu) che appiantisce il tutto a una moto con velocità uniforme.
Pertanto, la velocità media non fornisce informazioni sul reale moto del corpo.
Per saperne di più devo studiare la velocità istantanea del corpo.
B] La velocità media sul piano
Quando studio lo spostamento di un punto sul piano devo considerare lo spazio in due dimensioni (x,y).
Un esempio pratico
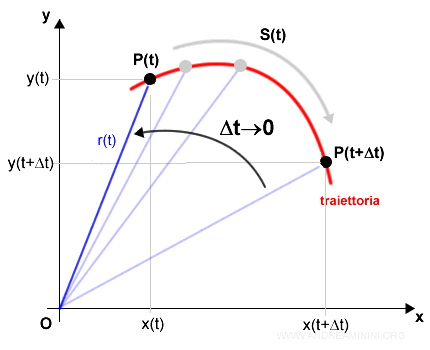
Ad esempio, un punto si sposta sul piano dalla posizione P(t) alla posizione P(t+Δt) in un intervallo di tempo Δt.
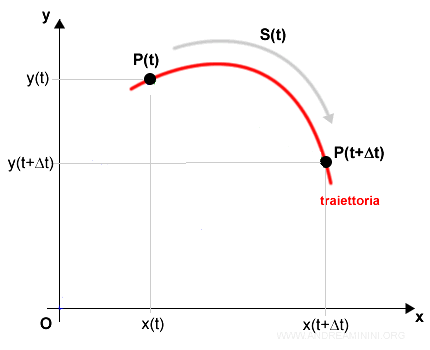
Attenzione. In questo diagramma le ascisse non misurano il tempo bensì la posizione x del corpo. Ci troviamo su un piano ossia in uno spazio a due dimensioni ( es. un tavolo ). In ogni istante temporale il punto occupa una posizione alle coordinate (x(t),y(t)) del piano. Poiché si sta spostando, le coordinate cambiano nel tempo. La traiettoria (rossa) è l'insieme delle coordinate occupate dal punto durante il suo cammino.
Nell'istante t il punto si trova alle coordinate (x(t),y(t)) mentre nell'istante t+Δt alle coordinate (x(t+Δt),y(t+Δt)).
Nella rappresentazione vettoriale le posizioni del punto nell'istante t e t+Δt sono individuate dai vettori r(t) e r(tΔt)
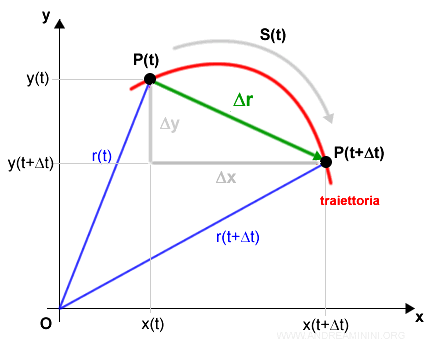
La velocità media è pari al rapporto incrementale Δr/Δt
$$ \frac{Δr}{Δt} = \frac{r(t+Δt)-r(t)}{Δt} $$
Questa grandezza vettoriale non è però uguale alla velocità effettiva del corpo, perché la traiettoria S(t) del punto non è lineare.
Per saperne di più sul reale moto del corpo devo calcolare la velocità istantanea in ogni punto della traiettoria.
La velocità istantanea
La velocità istantanea misura la variazione della posizione in un istante particolare.
A] La velocità istantanea sulla retta
A partire dalla velocità media, posso suddividere l'intervallo temporale t2-t1 in intervalli più piccoli.
In questo modo ottengo una curva della velocità che approssima quella reale, perché è composta da una serie di velocità medie.
Tuttavia, non si può ancora parlare di velocità istantanea.
Anche se l'intervallo temporale è più piccolo, si tratta ancora di velocità media.
Come calcolare la velocità istantanea
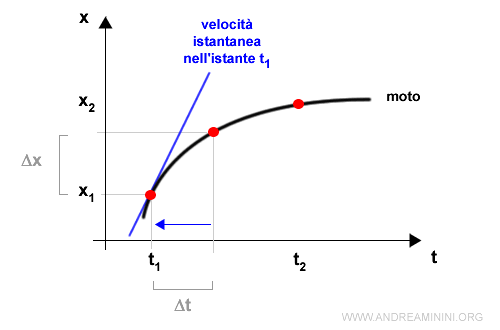
Per ottenere la velocità istantanea nel momento t devo calcolare il limite per Δt→0 del rapporto incrementale Δx/Δt.
$$ \lim_{Δt \rightarrow 0} \frac{Δx}{Δt} = \frac{dx}{dt} $$
Il limite coincide con il coefficiente angolare della retta tangente nell'istante t alla curva della velocità.
Posso seguire lo stesso metodo per calcolare la velocità istantanea in ogni istante t.
Basta calcolare il limite per Δt→0 del rapporto incrementale Δx/Δt. in ogni istante t.
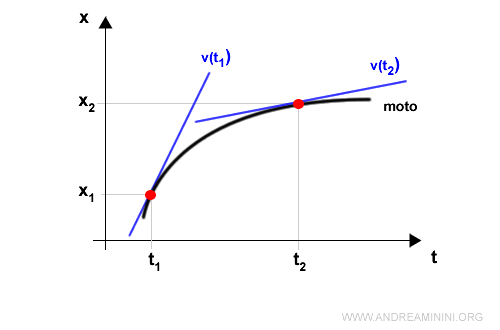
La seconda retta tangente è più orizzontale perché il punto ha ridotto la velocità rispetto all'istante iniziale.
Quando la retta tangente è completamente orizzontale, il punto è fermo alla posizione x e non si muove nel tempo.
Il coefficiente angolare della retta tangente (blu) indica la velocità istantanea del punto nell'istante t.
Come è noto dall'analisi matematica, il coefficiente angolare è in relazione con la derivata della funzione.
Pertanto, la velocità istantanea nel moto rettilineo nell'istante t coincide con la derivata dello spazio rispetto al tempo.
$$ v = \frac{dx}{dt} $$
- Nota. Il segno della derivata mi fornisce anche un'informazione aggiuntiva sul verso del moto:
- se v>0 la particella si sposta da destra verso sinistra
- se v<0 la particella si sposta da sinistra verso destra
B] La velocità istantanea sul piano
Per calcolare la velocità di un punto sul piano in un istante temporale t, devo rendere infinitesimale la variazione del tempo Δt.
Esempio
Un punto si sposta sul piano lungo una traiettoria S. Dopo un istante temporale Δt passa dalla posizione P(t) alla posizione P(t+Δt)
Queste due coordinate mi permettono di tracciare il vettore spostamento.

Nota. Il vettore spostamento è pari alla differenza tra i due raggi vettori. $$ Δr = OP(t+Δt) - OP(t) = r(t+Δt) - r(t) $$ La lunghezza del vettore spostamento è pari al suo modulo |Δr|. Come si può facilmente vedere, la lunghezza del vettore spostamento |Δr| è sempre minore o uguale alla lunghezza della traiettoria S. $$ |Δr| \le ΔS $$
Il vettore spostamento individua la velocità media del punto.
$$ \frac{Δr}{Δt} = \frac{r(t+Δt)-r(t)}{Δt} $$
Per individuare la velocità istantanea nel punto P(t) devo calcolare il limite del rapporto incrementale per Δt che tende a zero.
$$ \lim_{Δt \rightarrow 0} \frac{Δr}{Δt} = \lim_{Δt \rightarrow 0} \frac{r(t+Δt)-r(t)}{Δt} $$
Il limite sposta il raggio vettore r(t+Δt) a sinistra, fino a raggiungere una distanza infinitesimale rispetto al raggio r(t)
La formula precedente è la derivata del raggio vettore rispetto al tempo.
$$ \lim_{Δt \rightarrow 0} \frac{r(t+Δt)-r(t)}{Δt} = \frac{dr}{dt} $$
Essendo una derivata, mi fornisce l'inclinazione della retta tangente nel punto P(t).
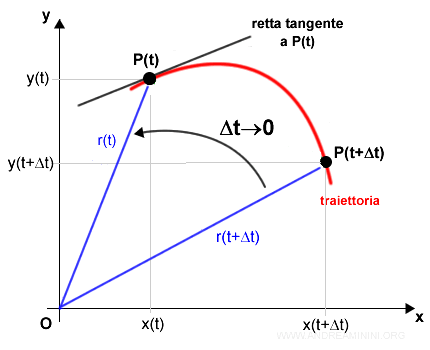
Nota. La derivata di una funzione f() in un punto è uguale al coefficiente angolare della retta tangente alla funzione f() nel punto stesso. Per un approfondimento sul significato geometrico della derivata.
In questo modo mi permette di conoscere la direzione, il verso e la velocità del corpo nell'istante t.
Studiando la velocità istantanea in ogni istante temporale posso ricostruire il moto del corpo come fosse una sequenza di spostamenti rettilinei infinitesimi.
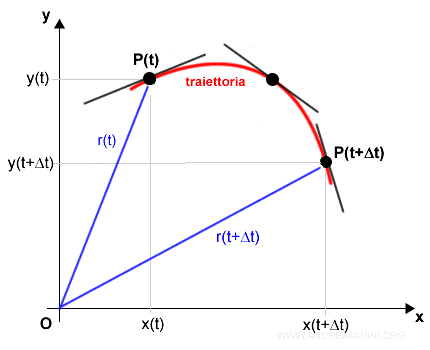
Le rette tangenti in ogni istante temporale, coincidono alla tangente della traiettoria nell'istante considerato
Considerando anche il versore della retta tangente (uT) posso conoscere la direzione istantanea del punto in ogni istante.
$$ v = \frac{ds}{dt} \cdot u_T $$
La velocità v è detta velocità vettoriale e individua il verso e la direzione del punto.
Spiegazione. Il versore uT indica la direzione del corpo verso destra (u=1) o sinistra (u=-1) lungo la retta tangente alla traiettoria nel punto P(t). Quindi, uno spostamento infinitesimale del raggio vettore r è uguale a uno spostamento nella traiettoria ds per il versore u. $$ dr = ds \cdot u_T $$
Il modulo della velocità vettoriale individua, invece, la velocità istantanea del punto
$$ v= \frac{ds}{dt} $$
E così via.
