Le trasformazioni di Galileo
Le trasformazioni di Galileo sono equazioni utilizzate per trasformare le coordinate di un punto nello spazio e nel tempo da un sistema di riferimento inerziale a un altro.
Sono anche note come trasformazioni galileiane.
Queste trasformazioni prendono il nome da Galileo Galilei, che le formulò per descrivere matematicamente come le leggi del moto sono le stesse in tutti i sistemi di riferimento inerziali, un principio noto come relatività galileiana.
Il presupposto è che i due sistemi si muovano l'uno rispetto all'altro a velocità costante in linea retta
Nota. I sistemi inerziali sono sistemi nei quali un corpo non soggetto a forze esterne si trova in stato di quiete o si muove con un moto rettilineo uniforme, a velocità costante ovvero senza accelerazione, in accordo con la prima legge del moto di Newton.
La forma più semplice delle trasformazioni di Galileo si applica a due sistemi di riferimento inerziali, \( S \) e \( S' \), dove \( S' \) si muove rispetto a \( S \) a una velocità costante \( v \) lungo l'asse \( x \).
Per semplicità ipotizzo che entrambi i sistemi di riferimento condividano lo stesso tempo t=t'.
Nell'istante iniziale t=0 le origini O=O' dei due sistemi di riferimento coincidono.
Ad esempio, il sistema di riferimento S è una stazione ferroviaria mentre il sistema di riferimento S' è un treno. I due sistemi coincidono quando il treno si trova alla stazione ferroviaria. Sono due sistemi di riferimento inerziali perché sono entrambi in stato di quiete.
In un istante successivo t>0 i due sistemi non coincidono più.
Ad esempio, il sistema di riferimento S' si sta spostando a velocità costante $ \vec{v} t' $ nel tempo, dove $ \vec{v} $ è il vettore della velocità.
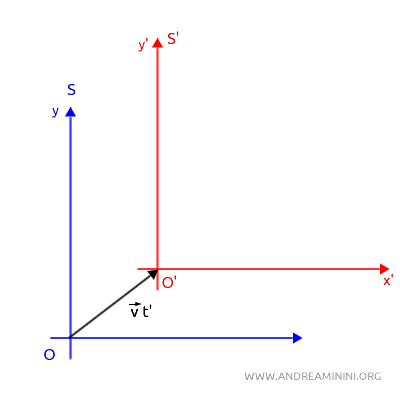
Nota. Ad esempio, il treno S' ha lasciato la stazione e ora viaggia a velocità costante. La stazione S resta, ovviamente, in stato di quiete. Pertanto, anche in questo caso i due sistemi S e S' sono sistemi inerziali.
La velocità dello spostamento è nettamente inferiore alla velocità della luce, quindi posso considerare il tempo come una grandezza assoluta (tempo assoluto) che scorre allo stesso modo in entrambi i sistemi di riferimento ossia t=t'.
In questa situazione i due sistemi di riferimento misurano lo spazio in modo diverso.
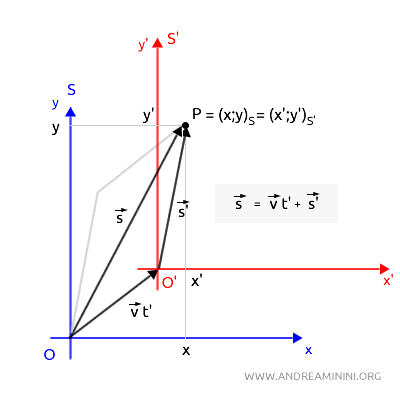
Ad esempio, nel sistema di riferimento S il punto P ha come coordinate (x;y) mentre nel sistema S' lo stesso punto ha come coordinate (x;y).
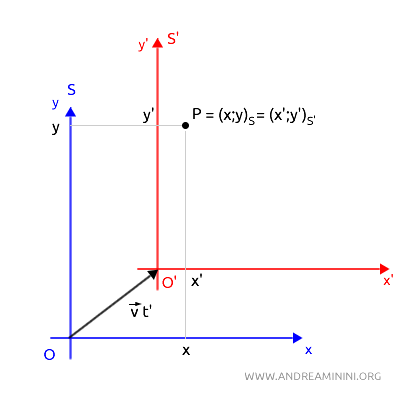
Per rappresentare la posizione del punto P nei sistemi di riferimento S e S' utilizzo due vettori di posizione $ \vec{s} $ e $ \vec{s}' $.
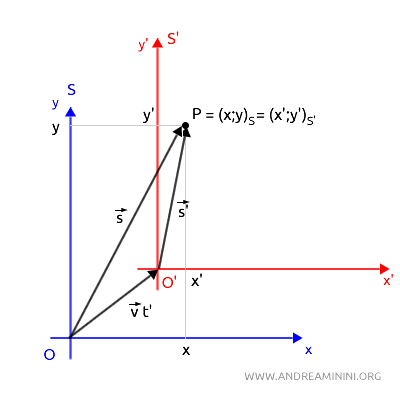
I due vettori $ \vec{s} $ e $ \vec{s}' $ indicano lo stesso punto P da due sistemi di riferimento diversi S e S'.
Come si può facilmente notare, esiste una relazione vettoriale tra i due sistemi di riferimento.
La posizione del punto P nel sistema di riferimento S è la somma vettoriale del vettore velocità $ \vec{v} $. e del vettore di posizione $ \vec{s}' $.
$$ \vec{s} = \vec{v}t' + \vec{s}' $$
La somma tra i due vettori si può facilmente calcolare in modo geometrico usando il metodo del parallelogramma o il metodo punta-coda.
Quindi, posso scrivere la relazione tra i due sistemi inerziali S e S' tramite il seguente sistema di equazioni:
$$ \begin{cases} \vec{s} = \vec{v}t' + \vec{s}' \\ \\ t = t' \end{cases} $$
Se un evento avviene al punto \( (x, y) \) e al tempo \( t \) in \( S \), e al punto \( (x', y') \) e al tempo \( t' \) in \( S' \), le trasformazioni di Galileo sono espresse dalle seguenti equazioni:
$$ \begin{cases} \vec{s}' = \vec{s} - \vec{v}t \\ \\ t' = t \end{cases} $$
Queste equazioni sono dette trasformazioni di Galileo e permettono di passare dal sistema di riferimento S a S' e viceversa.
La seconda equazione dei sistemi mostra che, secondo la meccanica classica, il tempo è assoluto e scorre allo stesso modo in tutti i sistemi di riferimento inerziali, il che significa che \( t' = t \).
Le trasformazioni di Galileo rimangono accurate per velocità molto inferiori alla velocità della luce. Tuttavia, quando le velocità coinvolte si avvicinano alla velocità della luce, le trasformazioni di Galileo non sono più sufficienti per descrivere accuratamente il comportamento dei corpi in movimento. In tali casi, le trasformazioni di Lorentz della relatività ristretta, proposte da Hendrik Lorentz, forniscono una descrizione più precisa, incorporando effetti come la dilatazione del tempo e la contrazione delle lunghezze.
Se entrambi i sistemi di riferimento inerziali S e S' sono in movimento, si nota anche una relazione tra la velocità di un oggetto misurata nei due sistemi.
Ad esempio, considero l'equazione vettoriale in un determinato lasso temporale Δt'
$$ \vec{s} = \vec{v} \Delta t' + \vec{s}' $$
Divido entrambi i membri dell'equazione per Δt'
$$ \frac{ \vec{s} }{ \Delta t' } = \frac{ \vec{v} \Delta t' }{ \Delta t' } + \frac{ \vec{s}' }{ \Delta t' } $$
$$ \frac{ \vec{s} }{ \Delta t' } = \vec{v} + \frac{ \vec{s}' }{ \Delta t' } $$
Il rapporto s/Δt' è il vettore velocità $ \vec{v}_S $ dell'oggetto nel sistema di riferimento S.
$$ \vec{v}_S = \vec{v} + \frac{ \vec{s}' }{ \Delta t' } $$
Il rapporto s'/Δt' è il vettore velocità $ \vec{v}_{S'} $ dell'oggetto nel sistema di riferimento S'.
$$ \vec{v}_S = \vec{v} + \vec{v}_{S'} $$
Questo dimostra che, in generale, la velocità $ \vec{v}_{S} $ di un oggetto osservata nel sistema di riferimento S è la risultante della somma vettoriale tra la sua velocità $ \vec{v}_{S'} $ nel sistema S′ e la velocità $ \vec{v} $ di S′ rispetto a S.
Esempio. Considero un'automobile A come un sistema di riferimento inerziale che si muove a 50 km/h lungo una strada, l'automobile B la sorpassa incrementando la propria velocità di 20 km/h rispetto a quella di A.

In questo contesto, per un osservatore esterno fermo rispetto alla strada, la velocità di B non è semplicemente la sua velocità relativa a A, ma piuttosto la somma delle velocità di A e B rispetto alla strada. Pertanto, se A viaggia a 50 km/h e B la supera con una velocità relativa di 20 km/h, l'automobile B si muove a una velocità totale di 70 km/h rispetto alla strada. $$ 70 \ km/h = 50 \ km/h + 20 \ km/h $$
E così via.
