Trasformazione di Laplace
La trasformazione di Laplace
Per risolvere le equazioni differenziali sono molto utili le trasformazioni funzionali che associano funzioni a funzioni.
Tra queste è molto usata la trasformazione di Laplace.
Una trasformazione funzionale crea una corrispondenza biunivoca tra le funzioni del tempo (funzioni oggetto) e delle funzioni immagine di diversa natura ma più semplici da risolvere.
La trasformazione di Laplace (L) associa dei valori reali/complessi F(s) a una funzione del tempo f(t).
$$ F(s) = L[f(t)] $$
Esempio. La trasformata di Laplace converte un'equazione differenziale del problema oggetto in un'equazione algebrica del problema immagine. E' chiaramente più semplice da risolvere.
Una volta trovata la soluzione al problema immagine, posso tradurla in una soluzione del problema oggetto tramite l'operazione di trasformazione inversa, detta antitrasformazione di Laplace.
$$ f(t)=L^{-1}[F(s)] $$
Le formule complete della trasformata e dell'antitrasformata di Laplace sono le seguenti:
$$ F(s) = L[f(t)] = \int_{0}^{∞} f(t)e^{-st} dt $$
$$ f(t)=L^{-1}[F(s)] = \frac{1}{2πj} \int_{σa-j∞}^{σa+j∞} F(s) e^{st} ds $$
Spesso non occorre fare dei calcoli per risolvere le trasformate di Laplace, in quanto esistono delle tabelle di conversione che mi permettono di risolvere gran parte dei problemi relativi allo studio dei sistemi.
La funzione F(s) è una funzione di variabile complessa ed è definita in un dominio (dominio di convergenza).
Le condizioni per usare la trasformazione di Laplace
- la funzione f(t) è nulla per t<0.
- la funzione f(t) è lineare. Date due costanti c1 e c2 e due funzioni f1(t) e f2(t) definite nel tempo con trasformata F1(s) e F(s) vale la relazione $$ L[c_1 f_1(t)+c_2 f_2(t)]=c_1 F_1(s) + c_2 F_2(s) $$
Nota. In presenza di valori coniugati s* della variabile complessa s, la funzione di Laplace F(s) assume valori coniugati $$ F(s*)=F*(s) $$
E così via.
Risposta all'impulso
La risposta dei sistemi lineari descritti da equazioni differenziali nella forma generale
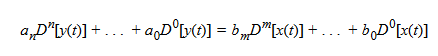
ha diverse proprietà interessanti.
- Se y(t) è la risposta del sistema al segnale x(t) a partire dalla condizione iniziale di quiete
- L'integrale y(t) è la risposta all'integrale del segnale di ingresso x(t).
- La derivata di y(t) è la risposta alla derivata del segnale di ingresso x(t).
Le risposte canoniche
Le risposte canoniche sono utili per studiare il comportamento dinamico del sistema risalire alla risposta a un segnale qualsiasi.
Sono risposte canoniche
- la risposta a gradino (o indiciale) $$ g_u(t) $$
- la risposta all'impulso di Dirac (o impulsiva). E' la derivata della risposta a gradino. $$ g(t) $$
Nota. Per essere derivabile la funzione di trasferimento deve essere un rapporto tra polinomi P/Q e il grado del polinomio al numeratore P deve essere inferiore rispetto a quello del polinomio al denominatore Q.
E così via
