Teorema del completamento della base vettoriale

Se la base vettoriale è incompleta, è sempre possibile espandere e completare la base vettoriale aggiungendo gli altri vettori linearmente indipendenti.

La definizione

In uno spazio vettoriale V di dimensione finita pari a n sul campo K, dato v₁,...,v_k vettori di V linearmente indipendenti, con k<n, allora esistono n-k vettori v_k+1,...,v_n di V, tali da formare una base di V insieme ai precedenti.
$$ B = \{ v_1,...,v_k,v_{k+1},...,v_n \} $$

Un esempio

Nello spazio vettoriale V=R³ nel campo R ho due vettori:

$$ v_1=(2,1,0) $$ $$ v_2=(1,1,0) $$

Sono due vettori linearmente indipendenti ma la base B è incompleta.

$$ B = \{ v_1 , v_2 , ? \} $$

Per trovare il vettore mancante, scrivo i due vettori sotto forma di matrice

$$ \begin{pmatrix} 2 & 1 \\ 1 & 1 \\ 0 & 0 \end{pmatrix} $$

Poi aggiungo alla matrice dei coefficienti la base canonica dello spazio vettoriale V=R³.

$$ \begin{pmatrix} 2 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix} $$

Nota. Qualsiasi altra base dello spazio vettoriale V=R³ andrebbe bene. E' comunque più pratico svolgere i calcoli con la base canonica essendo composta da una diagonale di uno.

A questo punto applico il metodo di eliminazione di Gauss-Jordan per trasformarla in una matrice a gradini.

$$ \begin{pmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix} $$

I pivot della matrice a gradini si trovano nella prima, nella seconda e nella quinta colonna.

Quindi, seleziono la prima, la seconda e la quinta colonna della matrice di origine.

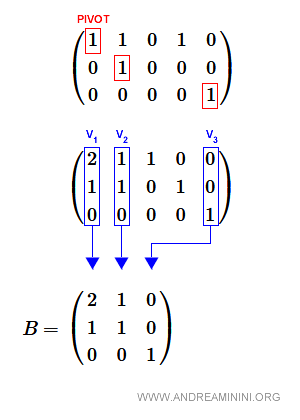
Ho così trovato il terzo vettore linearmente indipendente della base ossia v₃=(0,0,1).

La base completa è la seguente:

$$ B = \{ v_1 = (2,1,0) , v_2 = (1,1,0) , v_3=(0,0,1) \} $$

Ora il numero degli elementi della base eguaglia la dimensione dello spazio vettoriale V (n=3).