Le basi equiverse e contraverse
Uno spazio vettoriale V è composto da un insieme di vettori generati a partire da una base vettoriale B. Ogni spazio vettoriale può essere costruito su diverse basi.
Nota. A seconda della base prescelta, a ogni vettore dello spazio vettoriale sono associate coordinate diverse. Gli elementi del vettore restano però sempre gli stessi. Ad esempio, il vettore v(1,1) con la base B1 ha coordinate CB1=(x,y) mentre con la base B2 ha coordinate CB2=(x',y'). Le coordinate cambiano ma gli elementi v(1,1) sono costanti.
E' comunque possibile il passaggio da una base a un'altra tramite la matrice del cambio di base.
$$ C_{B_2}(v) = M_{B_1,B_2} \cdot C_{B_1}(v) $$
Nel cambiamento di base le basi sono dette:
- Basi equiverse. Se il determinante della matrice del cambio di base è maggiore di zero.
$$ det ( M_{B_1,B_2} ) > 0 $$
- Basi contraverse. Se il determinante della matrice del cambio di base è minore di zero.
$$ det ( M_{B_1,B_2} ) < 0 $$
L'insieme delle basi equiverse di uno spazio vettoriale è detto orientazione.
Lo spazio Rn è composto da due insiemi di basi equiverse tra loro. Scegliere un'orientazione vuol dire scegliere uno di questi insiemi ( equiverse o contraverse ).
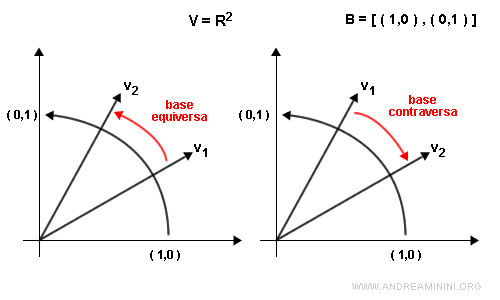
Esempio. Lo spazio R2 è un piano con un verso di rotazione fissato dal vettore (1,0) al vettore (0,1) della base canonica ( verso antiorario ). Per passare dal vettore v1 al vettore v2 si percorre l'angolo più piccolo. In una base equiversa si conserva il verso di rotazione del piano, mentre in una base contraversa si percorre il verso opposto. Pertanto, anche le basi contraverse sono equiverse tra loro pur essendo contraverse al verso di rotazione del piano. Sono una delle due possibili orientazioni nello spazio R2.
Un esempio pratico
Ho uno spazio vettoriale V nel campo K.
Calcolo il cambio di base da B1 a B2.
$$ B_1 = \{ \begin{pmatrix} 2 \\ 1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \end{pmatrix} \} $$
$$ B_2 = \{ \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \begin{pmatrix} -1 \\ 1 \end{pmatrix} \} $$
La matrice del cambio di base è la seguente:
$$ M_{B_1,B_2} = \begin{pmatrix} 1 & 2/3 \\ -1 & -1/3 \end{pmatrix} $$
Nota. Per vedere i passaggi rimando alla lettura degli appunti sulla matrice del passaggio di base.
Il determinante della matrice del cambio di base è positivo.
$$ det( M_{B_1,B_2} ) = 3 $$
Quindi sono due basi equiverse.
Viceversa, se il determinante fosse stato negativo sarebbero state basi controverse.
E così via.
