La serie di Mengoli
La serie di Mengoli è la seguente $$ \sum_{k=1}^n \frac{1}{k(k+1)} $$
Il limite per n che tende a infinito del termine generale della serie è uguale a zero.
La condizione necessaria (ma non sufficiente) della convergenza di una serie è soddisfatta.
Pertanto, la serie potrebbe essere convergente.
Per studiare il carattere di questa serie analizzo i primi valori della serie.
| k | ak | sn |
| 1 | $$ \frac{1}{2} $$ | $$ \frac{1}{2} $$ |
| 2 | $$ \frac{1}{6} $$ | $$ \frac{2}{3} $$ |
| 3 | $$ \frac{1}{12} $$ | $$ \frac{3}{4} $$ |
| 4 | $$ \frac{1}{20} $$ | $$ \frac{4}{5} $$ |
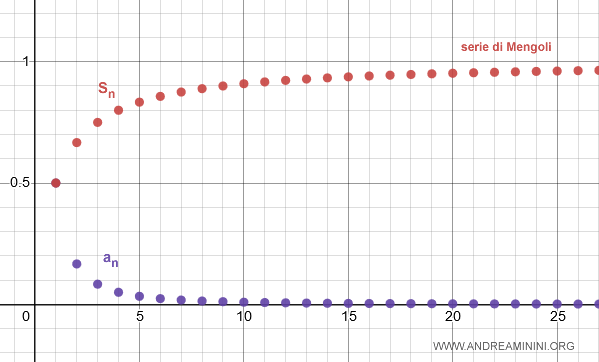
Guardando la successione delle ridotte n-esime della serie sn
$$ \frac{1}{2} , \frac{2}{3} , \frac{3}{4} , \frac{4}{5} , ... $$
ipotizzo che la somma sn per ogni n sia
$$ s_n = \frac{n}{n+1} $$
Per essere sicuro che sia vero
$$ \sum_{k=1}^n \frac{1}{k(k+1)} = \frac{n}{n+1} $$
utilizzo il metodo induttivo.
La base induttiva P(1) per k=1 è soddisfatta
$$ P(1) : \: \sum_{k=1}^1 \frac{1}{k(k+1)} = \frac{k}{k+1} $$
$$ P(1) : \: \frac{1}{1(1+1)} = \frac{1}{1+1} $$
$$ P(1) : \: \frac{1}{2} = \frac{1}{2} $$
Per ipotesi ritengo vera per qualsiasi n
$$ P(n) : \: \sum_{k=1}^n \frac{1}{k(k+1)} = \frac{n}{n+1} $$
A questo punto devo verificare se il passo induttivo è vero per n+1.
$$ P(n+1) : \: \sum_{k=1}^{n+1} \frac{1}{k(k+1)} = \frac{n}{n+1} $$
Provo a calcolare il valore di P(n+1)
$$ P(n+1) : \: \sum_{k=1}^{n+1} \frac{1}{k(k+1)} $$
che posso riscrivere in questa forma equivalente
$$ P(n+1) : \: [ \sum_{k=1}^{n} \frac{1}{k(k+1)} ] + \frac{1}{(n+1)((n+1)+1)} $$
$$ P(n+1) : \: [ \sum_{k=1}^{n} \frac{1}{k(k+1)} ] + \frac{1}{(n+1)(n+2)} $$
Il primo termine dell'addizione è la proposizione P(n)
$$ P(n+1) : \: P(n) + \frac{1}{(n+1)(n+2)} $$
Poiché P(n) è vera per ipotesi ed è uguale a n/n+1
$$ P(n+1) : \: \frac{n}{n+1} + \frac{1}{(n+1)(n+2)} $$
$$ P(n+1) : \: \frac{n(n+2)+1}{(n+1)(n+2)} $$
$$ P(n+1) : \: \frac{n^2+2n+1}{(n+1)(n+2)} $$
$$ P(n+1) : \: \frac{(n+1)^2}{(n+1)(n+2)} $$
$$ P(n+1) : \: \frac{n+1}{n+2} $$
che considerando n=n+1 equivale a
$$ P(n+1) : \: \frac{n}{n+1} $$
Questo dimostra l'uguaglianza tra la serie sn e n/(n+1) per qualsiasi n
$$ \sum_{k=1}^n \frac{1}{k(k+1)} = \frac{n}{n+1} $$
Ora per studiare il carattere della serie devo calcolare il limite per n tendente a infinito di sn.
$$ s = \lim_{n \rightarrow \infty} s_n $$
$$ s = \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k(k+1)} $$
Poiché sn=n/(n+1)
$$ s = \lim_{n \rightarrow \infty} \frac{n}{n+1} $$
Si tratta di una forma indeterminata ∞/∞
$$ s= \lim_{n \rightarrow \infty} \frac{n}{n+1} = \frac{∞}{∞} $$
che posso risolvere con il teorema di De L'Hopital
$$ s= \lim_{n \rightarrow \infty} \frac{D[n]}{D[n+1]} $$
$$ s= \lim_{n \rightarrow \infty} \frac{1}{1} = 1 $$
Il limite s esiste ed è un numero finito s=1
Quindi, la serie è convergente e la somma sn converge a 1 per n→∞.
E così via.
