Il teorema del rapporto delle serie

Data una successione a termini positivi, se esiste il limite della successione $$l = \lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n}$$ se il limite è minore di 1, la serie è convergente $$l<1 \Rightarrow \sum_{k=1}^{\infty} a_k < + \infty$$ se il limite è maggiore di 1, la serie è divergente $$l>1 \Rightarrow \sum_{k=1}^{\infty} a_k = + \infty$$

In questo teorema la successione è una successione a termini positivi.

A cosa serve il teorema?

E' uno dei criteri per studiare il carattere delle serie numeriche.

Attenzione. Se il limite è uguale a 1 il teorema del rapporto non fornisce nessuna informazione sul carattere della serie. In questo caso per studiare il carattere della serie devo usare un altro criterio di convergenza.

Un esempio pratico

Esempio 1

Prendo in considerazione la serie

$$\sum_{n=1}^{ \infty } \frac{n^2}{2^n}$$

La rispettiva successione è una succesione a termini positivi.

Applico il teorema del rapporto della serie calcolando il limite del rapporto di due termini consecutivi della successione

$$\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n}$$

dove

$$a_n = \frac{n^2}{2^n}$$

$$a_{n+1} = \frac{(n+1)^2}{2^{n+1}}$$

Pertanto il limite è

$$\lim_{n \rightarrow \infty} \frac{ \frac{(n+1)^2}{2^{n+1}} }{ \frac{n^2}{2^n} }$$

$$\lim_{n \rightarrow \infty} \frac{(n+1)^2}{2^{n+1}} \cdot \frac{2^n}{n^2}$$

$$\lim_{n \rightarrow \infty} \frac{(n+1)^2}{ 2 \cdot 2^n} \cdot \frac{2^n}{n^2}$$

$$\lim_{n \rightarrow \infty} \frac{(n+1)^2}{ 2 } \cdot \frac{1}{n^2}$$

$$\frac{1}{2} \cdot \lim_{n \rightarrow \infty} \frac{(n+1)^2}{ n^2 }$$

Il limite è una forma indeterminata ∞/∞

Per risolverlo utilizzo il teorema di De L'Hopital

$$\frac{1}{2} \cdot \lim_{n \rightarrow \infty} \frac{2n+2}{ 2n }$$

$$\frac{1}{2} \cdot \lim_{n \rightarrow \infty} \frac{2}{ 2 }$$

$$\frac{1}{2} \cdot 1$$

Il limite del rapporto esiste ed è un numero finito minore di uno.

$$\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n} = \frac{1}{2} < 1$$

Pertanto, secondo il teorema del rapporto la serie è convergente

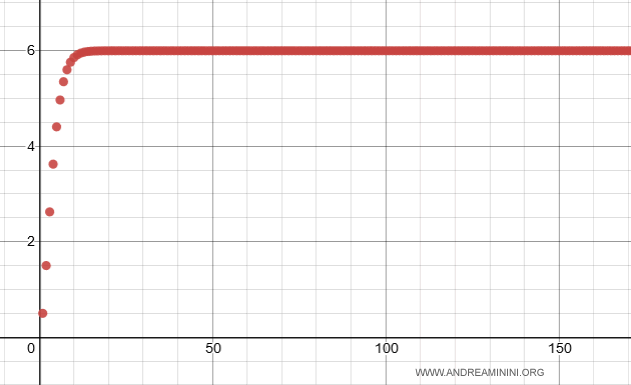
$$\sum_{n=1}^{ \infty } \frac{n^2}{2^n}$$

Ecco la rappresentazione grafica della serie

Esempio 2

Prendo in considerazione la serie

$$\sum_{n=1}^{ \infty } \frac{2^n}{n^5}$$

La rispettiva successione è una succesione a termini positivi.

Applico il teorema del rapporto delle serie

$$\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n}$$

dove

$$a_n = \frac{2^n}{n^5}$$

$$a_{n+1} = \frac{2^{n+1}}{(n+1)^5}$$

Quindi il limite del rapporto è

$$\lim_{n \rightarrow \infty} \frac{2^{n+1}}{(n+1)^5} \cdot \frac{n^5}{2^n}$$

$$\lim_{n \rightarrow \infty} \frac{2 \cdot n^5 }{(n+1)^5}$$

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ n^5 }{(n+1)^5}$$

Il limite è una forma indeterminata ∞/∞

Per risolverlo utilizzo il teorema di De L'Hopital

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ 5n^4 }{5(n+1)^4}$$

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ 4n^3 }{4(n+1)^3}$$

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ 3n^2 }{3(n+1)^2}$$

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ 2n }{2(n+1)}$$

$$2 \cdot \lim_{n \rightarrow \infty} \frac{ 1 }{1}$$

$$2 \cdot 1$$

Il limite del rapporto esiste ed è un numero finito maggiore di uno.

$$\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n} = 2 > 1$$

Pertanto, secondo il teorema del rapporto la serie è divergente

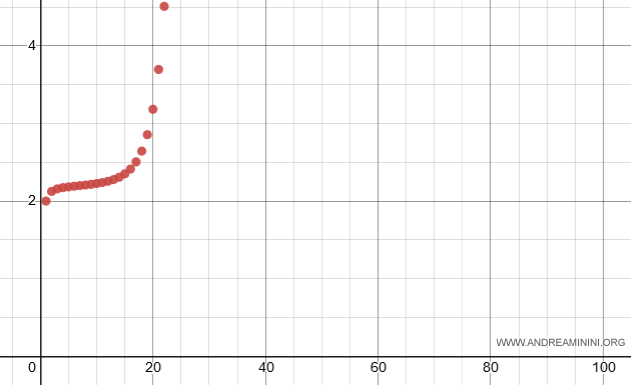
$$\sum_{n=1}^{ \infty } \frac{2^n}{n^5} = + \infty$$

Ecco la rappresentazione grafica della serie

La dimostrazione del teorema

Prendo in considerazione una generica serie a_k

$$\sum_{k=1}^{\infty} a_k$$

La successione a_k è a termini positivi

$$a_k < a_{k+1}$$

Poi studio l'ipotesi di convergenza e di divergenza usando come premessa il teorema del rapporto della serie.

Ipotesi 1 (convergenza)

Per ipotesi, il limite della successione a_k per n che tende a infinito esiste ed è minore di 1.

$$l = \lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n} < 1$$

Prendo in considerazione un numero x nell'intervallo (l,1) tale che

$$l < x < 1$$

Pertanto, esiste un indice v tale che per ogni n>v il rapporto tra due termini successivi della successione è minore di x

$$\frac{a_{n+1}}{a_n} < x$$

che equivale a dire

$$a_{n+1} < x \cdot a_n$$

Per ipotesi, l'indice v=1

Ne consegue che per ogni n>v (ossia n>1)

$$a_2 < x \cdot a_1 \\ a_3 < x \cdot a_2 \\ a_4 < x \cdot a_3 \\ \vdots$$

poiché a₂ < a₁ x posso riscrivere la successione dei termini in questo modo equivalente

$$a_2 < x \cdot a_1 \\ a_3 < x \cdot ( x \cdot a_1 ) \\ a_4 < x \cdot a_3 \\ \vdots$$

poi sostituisco a₃ con x·(x·a₁) e via dicendo

$$a_2 < x \cdot a_1 \\ a_3 < x \cdot ( x \cdot a_1 ) \\ a_4 < x \cdot ( x \cdot ( x \cdot a_1 ) ) \\ \vdots$$

ne consegue che

$$a_2 < x \cdot a_1 \\ a_3 < x^2 \cdot a_1 \\ a_4 < x^3 \cdot a_1 \\ \vdots$$

In generale ogni termine della successione è

$$a_n < x^{n-1} \cdot a_1$$

Calcolo la serie di entrambi i membri della disequazione

$$\sum_{n=1}^{ \infty } a_n < \sum_{n=1}^{ \infty } x^{n-1} \cdot a_1$$

La serie al secondo membro è la serie geometrica che è convergente a l' se la ragione x è compresa tra 0<x<1.

$$\sum_{n=1}^{ \infty } a_n < l'$$

Per il teorema del confronto delle serie anche la serie a_n al primo membro deve essere una serie convergente.

Ho così dimostrato la convergenza della serie.

Ipotesi 1 (divergenza)

Per ipotesi, il limite della successione a_k per n che tende a infinito esiste ed è maggiore di 1.

$$l = \lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n} > 1$$

Quindi, esiste un indice v tale che per ogni n>v

$$\frac{a_{n+1}}{a_n} > 1$$

che equivale a dire

$$a_{n+1} > a_n$$

Pertanto, la successione a_n è una successione monotòna strettamente crescente.

Il limite di una successione strettamente crescente non può convergere a zero per n→∞.

$$\lim_{n \rightarrow \infty} a_n \ne 0$$

Se la successione a_n non converge a zero, non è rispettata la condizione necessaria di convergenza delle serie.

Quindi, la serie associata alla successione a_n deve essere una serie divergente.

$$\sum_{n=1}^{\infty} a_n = + \infty$$

Ho dimostrato la divergenza della serie.

E così via