Esercizio: studio della serie numerica $ \sum_{n=1}^{\infty} \frac{2^n - 1}{2^n} $

Devo studiare la serie

$$ \sum_{n=1}^{\infty} \frac{2^n - 1}{2^n} $$

Il termine generale della serie è il seguente:

$$ a_n = \frac{2^n - 1}{2^n} $$

Semplifico il termine generale in questo modo:

$$ a_n = \frac{2^n - 1}{2^n} = \frac{2^n}{2^n} - \frac{1}{2^n} = 1 - \frac{1}{2^n} $$

A questo punto studio il limite della successione $ a_n $ per n che tende a infinito.

$$ \lim_{n \to \infty} a_n $$

$$ \lim_{n \to \infty} 1 - \frac{1}{2^n} $$

$$ \lim_{n \to \infty} 1 - \lim_{n \to \infty} \frac{1}{2^n} = 1 - 0 = 1 $$

Poiché il limite della successione è diverso da zero, deduco che la serie diverrge positivamente.

$$ \sum_{n=1}^{\infty} a_n = \sum_{n=1}^{\infty} \left(1 - \frac{1}{2^n}\right) = \sum_{n=1}^{\infty} 1 - \sum_{n=1}^{\infty} \frac{1}{2^n} $$

Quindi, la serie numerica è divergente.

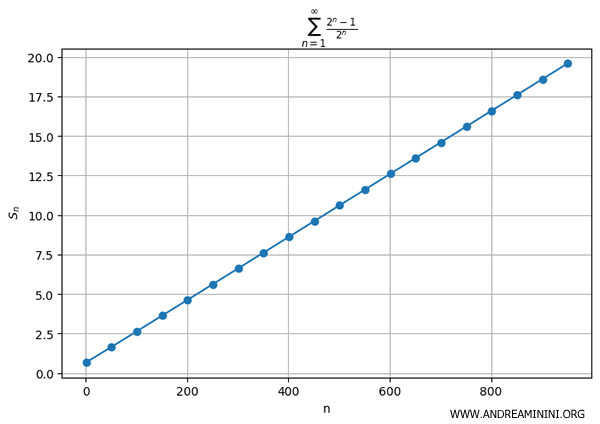
esempio

E così via.