Studio della convergenza della serie \( \sum_{n=1}^{\infty} \frac{n}{2n+1} \)
In questo esercizio devo studiare il carattere della serie
\[ \sum_{n=1}^{\infty} \frac{n}{2n+1} \]
Studiare il carattere della serie significa capire se converge, ossia ha somma finita, o diverge, ovvero ha la somma è infinita o non definita.
Per prima cosa analizzo il termine generale che in questo caso è:
\[ a_n = \frac{n}{2n+1} \]
Devo capire se questo termine tende a zero quando \( n \to \infty \). Questo è un requisito necessario affinché una serie possa convergere.
Quindi, calcolo il limite del termine generale.
\[ \lim_{n \to \infty} \frac{n}{2n+1} \]
In base al criterio necessario di convergenza, se una serie \( \sum a_n \) converge, allora necessariamente** \( \lim_{n \to \infty} a_n = 0 \). Se il limite non è zero, allora la serie diverge.
Per risolvere il limite divido il numeratore e il denominatore per \( n \) in modo da semplificare il rapporto.
\[ \lim_{n \to \infty} \frac{1}{2 + \frac{1}{n}} = \frac{1}{2 + 0} = \frac{1}{2} \]
Il limite del termine generale della serie non è zero ma \( \frac{1}{2} \).
\[\lim_{n \to \infty} a_n = \frac{1}{2} \neq 0 \]
Questo significa che è una serie a termini positivi, ma il termine generale non tende a zero.
Perciò, la serie $ \sum_{n=1}^{\infty} \frac{n}{2n+1} $ è divergente.
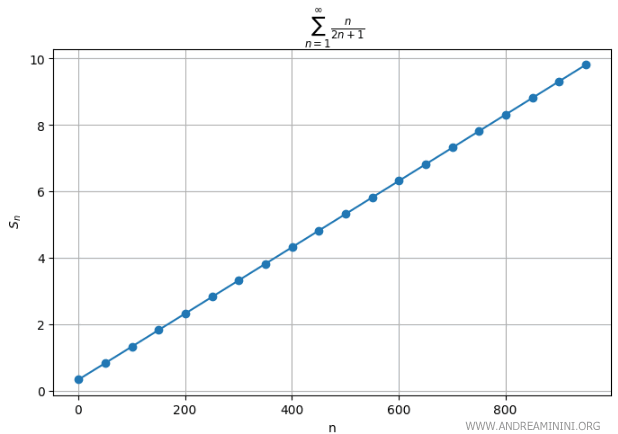
E così via-
