Esercizio limite di funzione di due variabili 4

Devo studiare il limite di questa funzione di due variabili per (x,y) che tende all'origine (0,0)

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

La funzione è:

\[ f(x,y) = \frac{xy^2}{x^2 + y^4} \]

Il numeratore \( xy^2 \) tende a \( 0 \) se \(x\) e \(y\) tendono a \(0\).

Il denominatore \( x^2 + y^4 \) è sempre positivo tranne in \((0,0)\), dove è nullo. Pertanto, nel punto (0,0) la funzione è indefinita.

Quindi, il limite è una forma indeterminata del tipo \(\frac{0}{0}\) e va analizzata più a fondo.

Soluzione 1

Provo a calcolare il limite lungo traiettorie diverse.

A] Caso 1: lungo la retta \(x = 0\)

Fisso x=0 nella funzione per muovermi lungo l'asse delle ordinate

\[ f(0,y) = \frac{0 \cdot y^2}{0 + y^4} = 0 \]

E' evidente che in questo caso il limite della funzione è zero.

\[ \lim_{(x,y)\to(0,0)} f(0,y)=0 \]

B]  Caso 2: lungo la retta \(y = 0\)

Ora fisso y=0 nella funzione per muovermi lungo l'asse delle ascisse

\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]

Anche in questo caso è evidente che il limite è zero.

\[ \lim_{(x,y)\to(0,0)} f(x,0)=0 \]

C]  Caso 3: lungo la retta \(y =x\)

Provo a vedere cosa succede se mi avvicino lungo la diagonale y=x

\[ f(x,x) = \frac{x \cdot x}{x^2 + x} = \frac{x^2}{x^2+x} = \frac{x^2}{x \cdot (1+x)} = \frac{x}{1+x} \]

Anche in questo caso il limite è zero.

\[ \lim_{(x,x)\to(0,0)} \frac{x}{1+x}=0 \]

E' sufficiente per affermare che il limite è zero? Assolutamente no! 

Le traiettorie per avvicinarsi al punto (0,0) sono infinite e non includono solo le rette ma anche curve di ogni tipo.

D]  Caso 4: lungo la parobola \(x =y^2 \)

Provo a vedere cosa accade lungo la curva \(x = y^2\)

\[ f(y^2, y) = \frac{y^2 \cdot y^2}{(y^2)^2 + y^4} = \frac{y^4}{y^4 + y^4} = \frac{y^4}{2y^4} = \frac{1}{2} \]

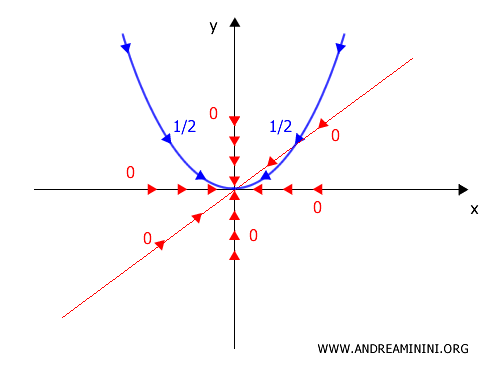
Lungo questa traiettoria, il limite non è 0, ma \(\frac{1}{2}\)

\[ \lim_{(x,y)\to(0,0)} f(y^2,y)=\frac{1}{2} \]

Ho trovato due traiettorie che restituiscono limiti diversi, quindi il limite non può esistere.

Soluzione 2

Il limite tende all'origine (0,0) quindi posso usare anche la tecnica delle coordinate polari.

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

Sostituisco le coordinate cartesiane \( (x,y) \) con le coordinatepolari \( x = \rho \cos \theta \) e \( y = \rho \sin \theta \)

\[ \lim_{\rho \to 0} \frac{( \rho \cos \theta ) \cdot ( \rho \sin \theta )^2}{( \rho \cos \theta )^2 + ( \rho \sin \theta )^4} \]

\[ \lim_{\rho \to 0} \frac{ \rho \cos \theta  \cdot \rho^2 \sin^2 \theta}{ \rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta } \]

\[ \lim_{\rho \to 0} \frac{\rho^3 \cos \theta \sin^2 \theta}{ \rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta } \]

\[ \lim_{\rho \to 0} \frac{\rho \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \]

\[ \lim_{\rho \to 0} \rho \cdot \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \]

In questo caso il limite non è indipendente da \( \theta \).

Ad esempio, se mantengo \( \theta \) costante la traiettoria è una retta e il limite per \( rho \to 0 \) è zero.

\[ \lim_{\rho \to 0} \rho \cdot \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } = 0 \]

Nota. Questo accade perché \( \cos \theta \sin^2 \theta \) e \( cos^2 \theta \) sono valori costanti che dipendono solo da \( \theta \) mentre \( \rho^2 \sin^4 \theta \) si annulla. Pertanto, il rapporto \( \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \) si annulla quando viene moltiplicato per \( \rho \to 0 \).

Se invece imposto una traiettoria \(  \cos\theta(\rho)=k\rho \) con \( k \neq 0  \) allora il denominatore diventa dell'ordine di  \( (k\rho)^{2}+\rho^{2}\sin^{4}\theta \) e il numeratore dell’ordine di \(\rho\cdot(k\rho)\sin^{2}\theta \).

\[ \lim_{\rho \to 0} \rho \cdot \frac{ (k \rho) \cdot \sin^2 \theta}{ (k \rho)^{2} + \rho^2 \sin^4 \theta } \]

Se \(  \cos\theta(\rho)=k\rho \) allora \( \sin \theta ( \rho ) = \sqrt{ 1 - \cos^2 \theta ( \rho )  } = \sqrt{1 - (k \rho } )^2  \).

Quindi, \( \sin^2 \theta ( \rho ) = 1 - (k \rho)^2 \) che per \( \rho \to 0 \) diventa \( \sin^2 \theta ( \rho )  \approx 1 \).

\[ \lim_{\rho \to 0} \rho \cdot \frac{ (k \rho) \cdot 1 }{ (k \rho)^{2} + \rho^2 \cdot 1} \]

\[ \lim_{\rho \to 0} \rho \cdot \frac{ k \rho }{ k^2 \rho^{2} + \rho^2 } \]

\[ \lim_{\rho \to 0}  \frac{ k \rho^2 }{ \rho^2 (k^2 +1) } \]

\[ \lim_{\rho \to 0}   \frac{ k  }{ k^2 +1 } =  \frac{ k  }{ k^2 +1 } \]

Ora il limite tende a \(k/(k^{2}+1)\) che è un valore finito e non nullo.

In conclusione, poiché lungo i raggi (θ costante) il limite è 0, mentre nella traiettoria curva \(  \cos\theta(\rho)=k\rho \) il limite è un numero finito \( \frac{ k  }{ k^2 +1 } \), deduco che il limite globale della funzione non esiste per \( (x,y) \to (0,0) \).

E così via.