Esercizi sui limiti delle funzioni di due variabili
Alcuni esercizi svolti sui limiti delle funzioni di due variabili
Esercizio 1
Devo calcolare il limite di questa funzione di due variabili
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} $$
Quando (x,y) tende a (0,0) il limite della funzione tende alla forma indeterminata 0/0
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = \frac{0}{0} $$
Per risolvere il limite adotto la tecnica del cambio di variabile.
Fisso la variabile t uguale a $ t =x^2+y^2 $
$$ t = x^2 + y^2 $$
In questo modo trasformo il limite della funzione f(x,y) nel limite notevole di una funzione f(t)
$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} $$
Il limite notevole di sen(t)/t è uguale a 1
$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} = 1 $$
Quindi anche il limite della funzione f(x,y) è uguale a 1.
Con un nuovo cambio di variabile sostituisco t con $ t=x^2+y^2 $
Il limite è risolto.
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = 1 $$
Esercizio 2
Devo studiare il limite di questa funzione f(x,y)
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} $$
Il limite è una forma indeterminata 0/0
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = \frac{0}{0} $$
Per studiarlo considero la disequazione tra la funzione f(x,y) e il valore assoluto della funzione
Nota. Data una qualsiasi funzione f(x,y) $$ -| f(x,y) | \le f(x,y) \le | f(x,y) | $$ Se il limite del valore assoluto |f(x,y)| è nullo, allora per il teorema dei carabineri anche il limite della funzione è nullo. $$ \lim_{(x,y) \rightarrow (0,0)} -| f(x,y) | \le \lim_{(x,y) \rightarrow (0,0)} f(x,y) \le \lim_{(x,y) \rightarrow (0,0)} | f(x,y) | $$ $$ 0 \le \lim_{(x,y) \rightarrow (0,0)} f(x,y) \le 0 $$
Devo verificare se il limite del valore assoluto è uguale a zero.
$$ \lim_{(x,y) \rightarrow (0,0)} | \frac{x^2y}{x^2+y^2} | $$
Il valore assoluto della funzione è sempre maggiore o uguale a zero.
$$ 0 \le | \frac{x^2y}{x^2+y^2} | $$
Riscrivo l'espressione in questa forma equivalente
$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} $$
Il secondo fattore x2/(x2+y2) è un numero compreso nell'intervallo (0,1) perché il denominatore è sempre maggiore del numeratore e tutti i termini sono positivi.
Quindi, il primo fattore |y| è moltiplicato per per un numero compreso nell'intervallo (0,1).
Di conseguenza la funzione è sempre minore o uguale a |y|
$$ 0 \le |y| \cdot \frac{x^2}{x^2+y^2} \le |y| $$
Calcolo il limite di tutti i membri della disequazione
$$ \lim_{(x,y) \rightarrow (0,0)} 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} \le \lim_{(x,y) \rightarrow (0,0)} |y| $$
Il primo e l'ultimo limite tendono a zero.
$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} \le 0 $$
Pertanto, per il teorema dei carabinieri anche il limite del valore assoluto tende a zero.
$$ \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} = 0 $$
$$ \lim_{(x,y) \rightarrow (0,0)} | \frac{x^2y}{x^2+y^2} | = 0 $$
Di conseguenza anche il limite della funzione iniziale tende a zero.
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = 0 $$
Spiegazione. Per il teorema dei carabinieri $$ \lim_{(x,y) \rightarrow (0,0)} - | \frac{x^2y}{x^2+y^2} | = 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} \le \lim_{(x,y) \rightarrow (0,0)} | \frac{x^2y}{x^2+y^2} | = 0 $$
Soluzione alternativa
Per calcolare il limite posso anche usare le coordinate polari.
\[ \lim_{(x,y) \to (0,0)} \frac{x^2 y}{x^2 + y^2} \]
Perché usare le coordinate polari? Le coordinate polari sono utili quando si lavora con limiti in due variabili che tendono a \((0,0)\), perché mi permettono di semplificare l’espressione e controllare meglio la dipendenza dalla distanza dall’origine.
Le coordinate polari delle variabili x e y sono
\[ x = \rho \cos \theta \]
\[ y = \rho \sin \theta \]
Dove \(\rho\) è la distanza dall’origine (\( \rho = \sqrt{x^2 + y^2} \)) e \(\theta\) è l’angolo rispetto all’asse \(x\)
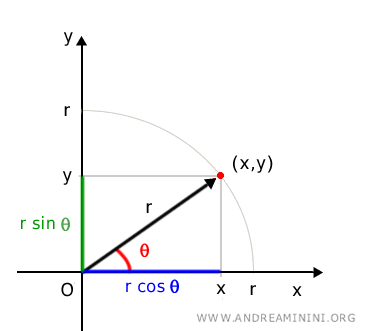
Inoltre, per il teorema di Pitagora
$$ r^2 = x^2+y^2 $$
Sostituisco \(x\) e \(y\) nella funzione:
\[ \frac{x^2 y}{x^2 + y^2} = \frac{(\rho \cos\theta)^2 (\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]
Svolgo i calcoli:
\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^2 \cos^2\theta \cdot \rho \sin\theta}{\rho^2 \cos^2\theta + \rho^2 \sin^2\theta} \]
\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2 (\cos^2\theta + \sin^2\theta)} \]
Per la prima relazione fondamentale della trigonometria $ \cos^2\theta + \sin^2\theta) = 1 $
\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2 \cdot 1} \]
\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2} \]
Quindi la funzione diventa:
\[ \frac{x^2 y}{x^2 + y^2} = \rho \cos^2\theta \sin\theta \]
A questo punto devo calcolare il limite
\[ \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta \]
In questo caso \(\theta\) è fissato, cioè indipendente da \(\rho\), e \(\cos^2\theta \sin\theta\) è un numero costante perché dipende solo da \(\theta\).
Quindi sto moltiplicando una costante per \(\rho\), che tende a zero \(\rho \to 0\).
Pertanto, il limite tende a zero.
\[ \cos^2\theta \sin\theta \cdot \lim_{\rho \to 0} \rho \to 0 \]
Per essere rigorosi, posso usare il teorema del confronto sapendo che \(\cos^2\theta \sin\theta\) è un numero tra \(-1\) e \(1\).
\[ -\rho \le \rho \cos^2\theta \sin\theta \le \rho \]
Calcolo il limite per \( \rho \to 0 \)
\[ \lim_{\rho \to 0} -\rho \le \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta \le \lim_{\rho \to 0} \rho \]
\[ - \lim_{\rho \to 0} \rho \le \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta \le \lim_{\rho \to 0} \rho \]
Poiché $ \lim_{\rho \to 0} \rho = 0 $ deduco che anche $ \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta = 0 $
\[ 0 \le \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta \le 0 \]
Il secondo metodo conferma il risultato del primo, ma in modo più elegante e diretto usando la variabile \(\rho\), che rappresenta la distanza da \((0,0)\).
Pertanto, il limite della funzione di due variabili tende a zero.
\[ \lim_{(x,y)\to(0,0)} \frac{x^2 y}{x^2 + y^2} = 0 \]
Esercizio 3
In questo esercizio devo studiare il limite di una funzione di due variabili
\[ \lim_{(x,y)\to(0,0)} \frac{xy}{x^2 + y^2} \]
Voglio capire se questo limite esiste e, in caso affermativo, dove converge.
Osservando la funzione mi accorgo subito che il numeratore: \(xy\) può essere positivo, negativo o zero, mentre il denominatore è positivo \(x^2 + y^2 > 0\) per \((x,y) \ne (0,0)\).
\[ f(x,y) = \frac{xy}{x^2 + y^2} \]
Quindi, la funzione è definita ovunque tranne in \((0,0)\).
Soluzione 1
Un buon modo per vedere se un limite esiste è calcolarlo lungo diverse curve che tendono a \((0,0)\), perché se ottengo risultati diversi il limite non esiste.
A] Caso 1: lungo la retta \(y = 0\)
Fisso y=0 e studio il limite lungo questa traiettoria.
\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]
Quindi lungo \(y = 0\) il limite della funzione è zero:
\[ \lim_{x \to 0} f(x,0) = 0 \]
B] Caso 2: lungo la retta \(y = x\)
Fisso \(y = x\) nella funzione:
\[ f(x,x) = \frac{x \cdot x}{x^2 + x^2} = \frac{x^2}{2x^2} = \frac{1}{2} \]
Quindi lungo la traitettoria \(y = x\) il risultato è \( \frac{1}{2} \)
\[ \lim_{x \to 0} f(x,x) = \frac{1}{2} \]
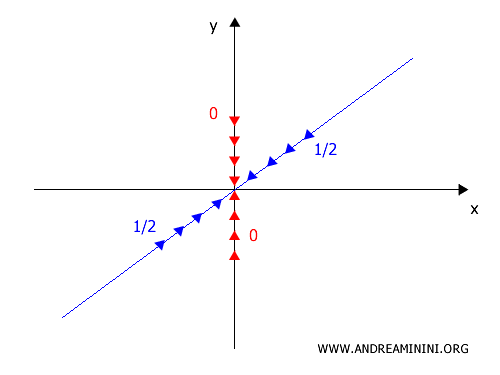
Da questo risultato deduco che il limite non esiste perché ho ottenuto risultati diversi da due traiettorie differenti.
- lungo \(y=0\) → \(0\)
- lungo \(y=x\) → \(\frac{1}{2}\)
Se il limite dipende dal percorso, allora NON esiste.
Soluzione 2
In questo caso il limite è verso l'origine (0,0), quindi posso risolverlo usando le coordinate polari delle variabili x e y.
\[ x = \rho \cos\theta \]
\[ y = \rho \sin\theta \]
Nota. Le coordinate polari funzionano bene solo se il punto in cui calcolo il limite è l’origine (0,0). Se voglio calcolare un limite in un punto diverso con le coordinate polari, devo prima traslare il sistema di coordinate.
Sostituisco le variabili nella funzione
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{(\rho \cos\theta)(\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 (\cos^2\theta + \sin^2\theta) } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 \cdot 1 } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \cos\theta \sin\theta \]
Quindi il limite è equivalente a:
\[ \lim_{\rho \to 0} f(x,y) = \cos\theta \sin\theta \]
E' subito evidente che la funzione $ \cos\theta \sin\theta $ non dipende da \(\rho\), ma da \(\theta\).
E poiché \(\theta\) rappresenta la direzione, allora il limite dipende dalla direzione, quindi il limite non esiste perché lungo traiettorie diverse dà risultati diversi.
Esercizio 4
Devo studiare il limite di questa funzione di due variabili per (x,y) che tende all'origine (0,0)
\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]
La funzione è:
\[ f(x,y) = \frac{xy^2}{x^2 + y^4} \]
Il numeratore \( xy^2 \) tende a \( 0 \) se \(x\) e \(y\) tendono a \(0\).
Il denominatore \( x^2 + y^4 \) è sempre positivo tranne in \((0,0)\), dove è nullo. Pertanto, nel punto (0,0) la funzione è indefinita.
Quindi, il limite è una forma indeterminata del tipo \(\frac{0}{0}\) e va analizzata più a fondo.
Soluzione 1
Provo a calcolare il limite lungo traiettorie diverse.
A] Caso 1: lungo la retta \(x = 0\)
Fisso x=0 nella funzione per muovermi lungo l'asse delle ordinate
\[ f(0,y) = \frac{0 \cdot y^2}{0 + y^4} = 0 \]
E' evidente che in questo caso il limite della funzione è zero.
\[ \lim_{(x,y)\to(0,0)} f(0,y)=0 \]
B] Caso 2: lungo la retta \(y = 0\)
Ora fisso y=0 nella funzione per muovermi lungo l'asse delle ascisse
\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]
Anche in questo caso è evidente che il limite è zero.
\[ \lim_{(x,y)\to(0,0)} f(x,0)=0 \]
C] Caso 3: lungo la retta \(y =x\)
Provo a vedere cosa succede se mi avvicino lungo la diagonale y=x
\[ f(x,x) = \frac{x \cdot x}{x^2 + x} = \frac{x^2}{x^2+x} = \frac{x^2}{x \cdot (1+x)} = \frac{x}{1+x} \]
Anche in questo caso il limite è zero.
\[ \lim_{(x,x)\to(0,0)} \frac{x}{1+x}=0 \]
E' sufficiente per affermare che il limite è zero? Assolutamente no!
Le traiettorie per avvicinarsi al punto (0,0) sono infinite e non includono solo le rette ma anche curve di ogni tipo.
D] Caso 4: lungo la parobola \(x =y^2 \)
Provo a vedere cosa accade lungo la curva \(x = y^2\)
\[ f(y^2, y) = \frac{y^2 \cdot y^2}{(y^2)^2 + y^4} = \frac{y^4}{y^4 + y^4} = \frac{y^4}{2y^4} = \frac{1}{2} \]
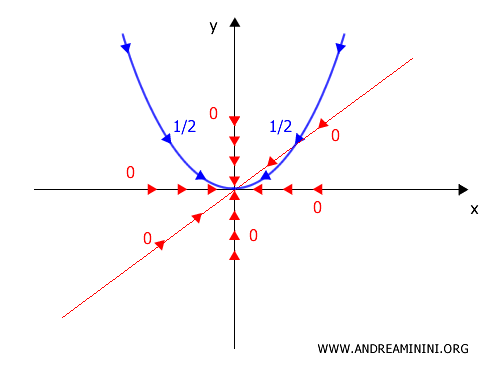
Lungo questa traiettoria, il limite non è 0, ma \(\frac{1}{2}\)
\[ \lim_{(x,y)\to(0,0)} f(y^2,y)=\frac{1}{2} \]
Ho trovato due traiettorie che restituiscono limiti diversi, quindi il limite non può esistere.
Soluzione 2
Il limite tende all'origine (0,0) quindi posso usare anche la tecnica delle coordinate polari.
\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]
Sostituisco le coordinate cartesiane \( (x,y) \) con le coordinatepolari \( x = \rho \cos \theta \) e \( y = \rho \sin \theta \)
\[ \lim_{\rho \to 0} \frac{( \rho \cos \theta ) \cdot ( \rho \sin \theta )^2}{( \rho \cos \theta )^2 + ( \rho \sin \theta )^4} \]
\[ \lim_{\rho \to 0} \frac{ \rho \cos \theta \cdot \rho^2 \sin^2 \theta}{ \rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta } \]
\[ \lim_{\rho \to 0} \frac{\rho^3 \cos \theta \sin^2 \theta}{ \rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta } \]
\[ \lim_{\rho \to 0} \frac{\rho \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \]
\[ \lim_{\rho \to 0} \rho \cdot \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \]
In questo caso il limite non è indipendente da \( \theta \).
Ad esempio, se mantengo \( \theta \) costante la traiettoria è una retta e il limite per \( rho \to 0 \) è zero.
\[ \lim_{\rho \to 0} \rho \cdot \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } = 0 \]
Nota. Questo accade perché \( \cos \theta \sin^2 \theta \) e \( cos^2 \theta \) sono valori costanti che dipendono solo da \( \theta \) mentre \( \rho^2 \sin^4 \theta \) si annulla. Pertanto, il rapporto \( \frac{ \cos \theta \sin^2 \theta}{ \cos^2 \theta + \rho^2 \sin^4 \theta } \) si annulla quando viene moltiplicato per \( \rho \to 0 \).
Se invece imposto una traiettoria \( \cos\theta(\rho)=k\rho \) con \( k \neq 0 \) allora il denominatore diventa dell'ordine di \( (k\rho)^{2}+\rho^{2}\sin^{4}\theta \) e il numeratore dell’ordine di \(\rho\cdot(k\rho)\sin^{2}\theta \).
\[ \lim_{\rho \to 0} \rho \cdot \frac{ (k \rho) \cdot \sin^2 \theta}{ (k \rho)^{2} + \rho^2 \sin^4 \theta } \]
Se \( \cos\theta(\rho)=k\rho \) allora \( \sin \theta ( \rho ) = \sqrt{ 1 - \cos^2 \theta ( \rho ) } = \sqrt{1 - (k \rho } )^2 \).
Quindi, \( \sin^2 \theta ( \rho ) = 1 - (k \rho)^2 \) che per \( \rho \to 0 \) diventa \( \sin^2 \theta ( \rho ) \approx 1 \).
\[ \lim_{\rho \to 0} \rho \cdot \frac{ (k \rho) \cdot 1 }{ (k \rho)^{2} + \rho^2 \cdot 1} \]
\[ \lim_{\rho \to 0} \rho \cdot \frac{ k \rho }{ k^2 \rho^{2} + \rho^2 } \]
\[ \lim_{\rho \to 0} \frac{ k \rho^2 }{ \rho^2 (k^2 +1) } \]
\[ \lim_{\rho \to 0} \frac{ k }{ k^2 +1 } = \frac{ k }{ k^2 +1 } \]
Ora il limite tende a \(k/(k^{2}+1)\) che è un valore finito e non nullo.
In conclusione, poiché lungo i raggi (θ costante) il limite è 0, mentre nella traiettoria curva \( \cos\theta(\rho)=k\rho \) il limite è un numero finito \( \frac{ k }{ k^2 +1 } \), deduco che il limite globale della funzione non esiste per \( (x,y) \to (0,0) \).
E così via.
