Esercizio limite di funzione di due variabili 3
In questo esercizio devo studiare il limite di una funzione di due variabili
\[ \lim_{(x,y)\to(0,0)} \frac{xy}{x^2 + y^2} \]
Voglio capire se questo limite esiste e, in caso affermativo, dove converge.
Osservando la funzione mi accorgo subito che il numeratore: \(xy\) può essere positivo, negativo o zero, mentre il denominatore è positivo \(x^2 + y^2 > 0\) per \((x,y) \ne (0,0)\).
\[ f(x,y) = \frac{xy}{x^2 + y^2} \]
Quindi, la funzione è definita ovunque tranne in \((0,0)\).
Soluzione 1
Un buon modo per vedere se un limite esiste è calcolarlo lungo diverse curve che tendono a \((0,0)\), perché se ottengo risultati diversi il limite non esiste.
A] Caso 1: lungo la retta \(y = 0\)
Fisso y=0 e studio il limite lungo questa traiettoria.
\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]
Quindi lungo \(y = 0\) il limite della funzione è zero:
\[ \lim_{x \to 0} f(x,0) = 0 \]
B] Caso 2: lungo la retta \(y = x\)
Fisso \(y = x\) nella funzione:
\[ f(x,x) = \frac{x \cdot x}{x^2 + x^2} = \frac{x^2}{2x^2} = \frac{1}{2} \]
Quindi lungo la traitettoria \(y = x\) il risultato è \( \frac{1}{2} \)
\[ \lim_{x \to 0} f(x,x) = \frac{1}{2} \]
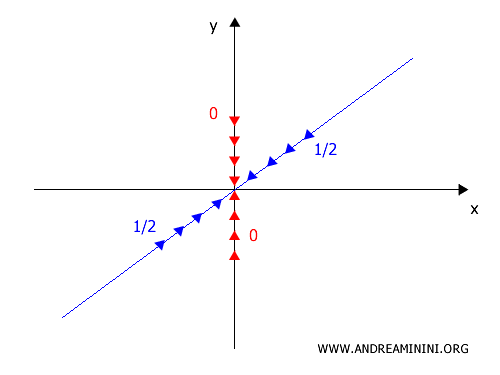
Da questo risultato deduco che il limite non esiste perché ho ottenuto risultati diversi da due traiettorie differenti.
- lungo \(y=0\) → \(0\)
- lungo \(y=x\) → \(\frac{1}{2}\)
Se il limite dipende dal percorso, allora NON esiste.
Soluzione 2
In questo caso il limite è verso l'origine (0,0), quindi posso risolverlo usando le coordinate polari delle variabili x e y.
\[ x = \rho \cos\theta \]
\[ y = \rho \sin\theta \]
Nota. Le coordinate polari funzionano bene solo se il punto in cui calcolo il limite è l’origine (0,0). Se voglio calcolare un limite in un punto diverso con le coordinate polari, devo prima traslare il sistema di coordinate.
Sostituisco le variabili nella funzione
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{(\rho \cos\theta)(\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 (\cos^2\theta + \sin^2\theta) } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 \cdot 1 } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{ \rho^2 \cos\theta \sin\theta }{ \rho^2 } \]
\[ f(x,y) = \frac{xy}{x^2 + y^2} = \cos\theta \sin\theta \]
Quindi il limite è equivalente a:
\[ \lim_{\rho \to 0} f(x,y) = \cos\theta \sin\theta \]
E' subito evidente che la funzione $ \cos\theta \sin\theta $ non dipende da \(\rho\), ma da \(\theta\).
E poiché \(\theta\) rappresenta la direzione, allora il limite dipende dalla direzione, quindi il limite non esiste perché lungo traiettorie diverse dà risultati diversi.
E così via.
