Prisma retto
Un prisma retto è un solido geometrico che ha due basi parallele e congruenti e dei rettangoli come facce laterali.
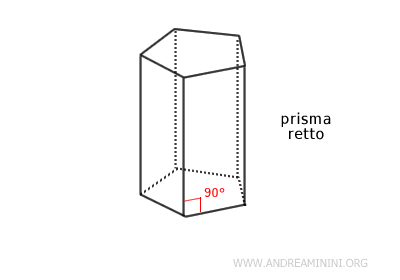
Le due basi possono essere di qualsiasi forma, ma sono solitamente poligoni (come triangoli, quadrati, pentagoni, ecc.). Sono identiche nella forma e nella dimensione e sono parallele tra loro.
Tutte le facce laterali sono, invece, dei rettangoli. Il numero di facce laterali è uguale al numero di lati della forma della base.
Il prisma retto è un caso particolare di prisma, in cui le facce laterali sono perpendicolari alle basi, il che significa che gli angoli tra le basi e le facce laterali sono tutti angoli retti (90 gradi). Grazie alla sua struttura semplice e regolare, ha molte applicazioni pratiche. Ad esempio, è molto utilizzato in architettura e nel design.
L'altezza del prisma è la distanza perpendicolare tra le due basi.
Le formule del prisma retto
Queste sono le principali formule applicabili al prisma retto:
- Area laterale
La superficie laterale del prisma retto si può calcolare moltiplicando il perimetro di base (P=2p) per l'altezza (h) del prisma $$ A_L = P \cdot h $$ - Area totale
La superficie totale del prisma retto è uguale alla somma tra l'area laterale (AL) e il doppio dell'area di base (2AB). In altre parole, è la somma delle aree di tutte le facce, incluse le basi. $$ A = A_L + 2A_B $$ - Volume
Il volume del prisma retto si calcola moltiplicando l'area di una delle basi (AB) per l'altezza (h) del prisma. $$ V = A_b \cdot h $$
Un esempio pratico
Questo prisma retto a base pentagonale ha uno spigolo di base lungo l=3 cm mentre l'altezza del prisma è h=10 cm.
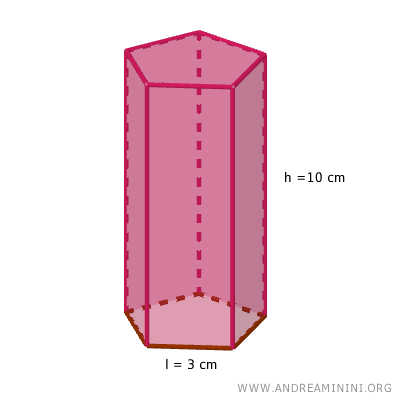
Devo calcolare la superficie totale e il volume del prisma.
Per prima cosa, calcolo il perimetro di base (PB) e l'area di base (AB). Essendo un prisma, va bene una qualsiasi delle due basi in quanto sono congruenti per definizione.
La base del prisma è un pentagono in cui ogni lato ha una lunghezza pari a 3 cm.
Quindi, il perimetro della base (PB) è la somma di tutti i cinque lati del poligono ossia 15 cm.
$$ P_B = 3 \cdot 5 = 15 \ cm $$
Per calcolare l'area del pentagono, trovo l'apotema del pentagono, sapendo che il lato del pentagono è l=3 cm e il numero fisso dei pentagoni regolari è all'incirca f=0.688
$$ a = 3 \cdot 0.688 = 2.064 $$
Una volta trovato l'apotema (circa a=2.064) lo moltiplico per il semiperimetro del pentagono p=PB/2, dove PB=15 cm, e ottengo l'area del pentagono ossia l'area di base del prisma (AB).
$$ A_B = a \cdot \frac{P}{2} $$
$$ A_B = 2.064 \cdot \frac{15}{2} = 15.48 \ cm^2 $$
A questo punto ho tutti gli elementi per calcolare l'area totale e il volume del prisma retto.
L'area laterale (AL) del prisma la ottengo moltiplicando il perimetro di base (PB=15 cm) per l'altezza (h=10 cm).
$$ A_L = P_B \cdot h $$
$$ A_L = 15 \ cm \cdot 10 \ cm = 150 \ cm^2 $$
L'area totale (A) del prisma è la somma dell'area laterale (AL) e del doppio dell'area di base (2AB) dove AB=15.48 cm2.
$$ A = A_L + 2 A_B $$
$$ A = 150 \ cm^2 + 2 \cdot (15.48 \ cm^2) $$
$$ A = 150 \ cm^2 + 30.96 \ cm^2 $$
Quindi, l'area totale del prisma è circa 180.96 cm2
$$ A = 180.96 \ cm^2 $$
Infine, il volume del prisma lo ricavo moltiplicando l'area di base (AB=15.48 cm2) per l'altezza (h=10 cm).
$$ V = A_B \cdot h $$
$$ V = 15.48 \ cm^2 \cdot 10 \ cm $$
Pertanto, il volume del prisma è circa 154.8 cm3
$$ V = 154.8 \ cm^3 $$
E così via
