Versori e coseni direttori

Una retta è orientata se ha un vettore direttore che determina il verso di percorrenza.

Questa è l'equazione vettoriale di una retta

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

Il vettore direttore della retta è

$$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

Tuttavia, questo vettore ha due possibili versi.

$$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

$$ -v_r = \begin{pmatrix} -l \\ -m \end{pmatrix} $$

A seconda dei casi ottengo una retta in un verso o nel verso opposto.

Nota. Il vettore direttore può essere concorde o meno con l'orientazione della retta.

Perché si parla di versore direttore?

Se un vettore ha la norma unitaria è detto versore.

Quindi, un versore direttore è un vettore direttore con norma uguale a uno.

$$ || v_r || = \sqrt{l^2 + m^2} = 1 $$

Per trasformare qualsiasi vettore in un versore, basta dividerlo per la sua norma.

$$ u_r = \frac{v_r}{|| v_r ||} $$

Gli elementi del versore direttore sono detti coseni direttori.

$$ u_r = \begin{pmatrix} r_x \\ r_y \end{pmatrix} $$

Perché sono detti coseni direttori?

Sono detti coseni direttori perché eguagliano i coseni degli angoli determinati dalla retta orientata e gli assi orientati.

Un esempio pratico

Ho una retta con l'equazione cartesiana.

La retta è orientata con x crescenti e y crescenti.

$$ 2x + 4y - 8 = 0 $$

Si tratta di un'equazione cartesiana, quindi il vettore direttore si ottiene tramite il vettore normale.

Il vettore normale è

$$ n = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Quindi la retta ha due possibili vettori direttori

$$ v_{r1} = \begin{pmatrix} -4 \\ 2 \end{pmatrix} $$

$$ v_{r2} = \begin{pmatrix} 4 \\ -2 \end{pmatrix} $$

Perché? Il vettore direttore e il vettore normale sono vettori ortogonali. Pertanto, il loro prodotto scalare <n, v> è uguale a zero. $$ < n , v_{r1} > = 2 \cdot (-4) + 4 \cdot 2 = 8 - 8 = 0 $$ $$ < n , v_{r2} > = 2 \cdot 4 + 4 \cdot (-2) = 8 - 8 = 0 $$

Guardando il diagramma cartesiano tutto diventa più chiaro.

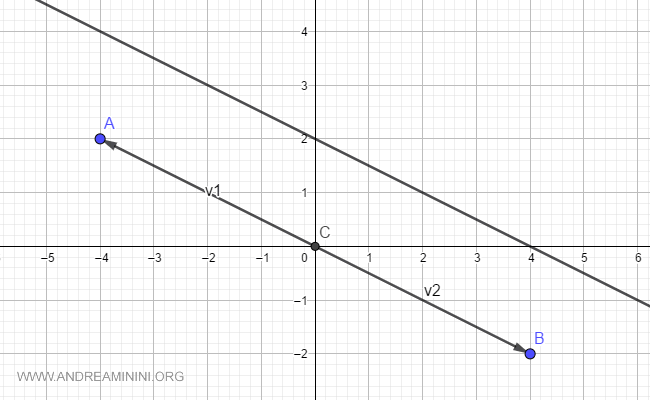
Quale scegliere? Dipende dall'orientazione della retta. Il vettore direttore v₁ è concorde con la retta orientata con x decrescenti e y crescenti. Viceversa, il vettore direttore v₂ è concorde con la retta orientata con x crescenti e y decrescenti. Posso prendere anche un vettore non concorde con l'orientazione della retta ma, in questo caso, va moltiplicato per -1 ossia -v₁ o -v₂.

Fisso l'orientazione della retta con y crescenti e x decrescenti.

Quindi, scelgo il vettore direttore v_r1 concorde con l'orientazione della retta.

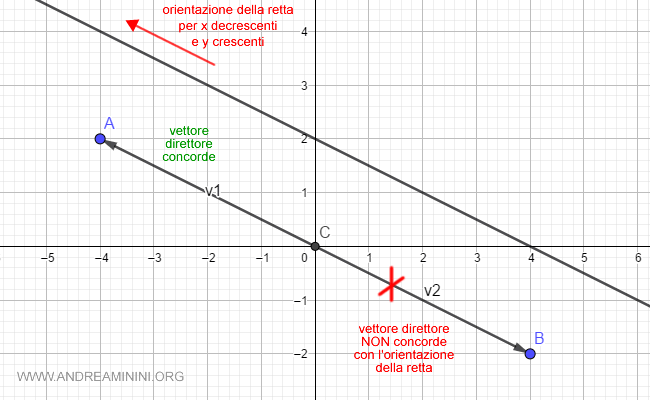
Nota. Potrei scegliere anche il vettore direttore non concorde v₂ moltiplicato per -1 ( ossia -v₂ ) ma sarebbe comunque come scegliere v₁. $$ - v_2 = -1 \cdot \begin{pmatrix} 4 \\ -2 \end{pmatrix} = \begin{pmatrix} -4 \\ 2 \end{pmatrix} = v_1 $$

Verifico se il vettore direttore v₁ è un versore ossia se ha la norma unitaria.

$$ || v_{r1} || = \sqrt{(-4)^2 + (2)^2} = \sqrt{20} $$

Non è un versore.

A questo punto, per trasformarlo in un versore lo divido per la sua norma.

$$ u_{r1} = \frac{v_{r1}}{|| v_{r1} ||} $$

$$ u_{r1} = \frac{ \begin{pmatrix} -4 \\ 2 \end{pmatrix} } { \sqrt{20} } = \begin{pmatrix} \frac{-4}{ \sqrt{20} } \\ \frac{2}{ \sqrt{20} } \end{pmatrix} $$

Ho così ottenuto il versore direttore u_r1.

E' un vettore proporzionale al vettore direttore v₁ ma ha un modulo uguale a 1.

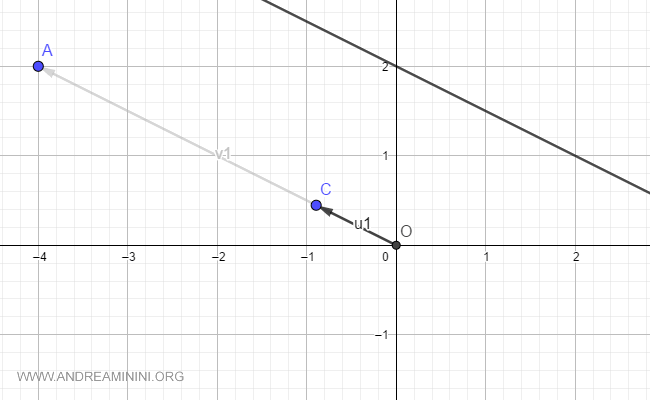
Nota. Il versore direttore è molto utile perché ha un modulo pari a uno e mi permette di usare le funzioni e le formule della trigonometria ( seno, coseno, tangente, ecc. ).

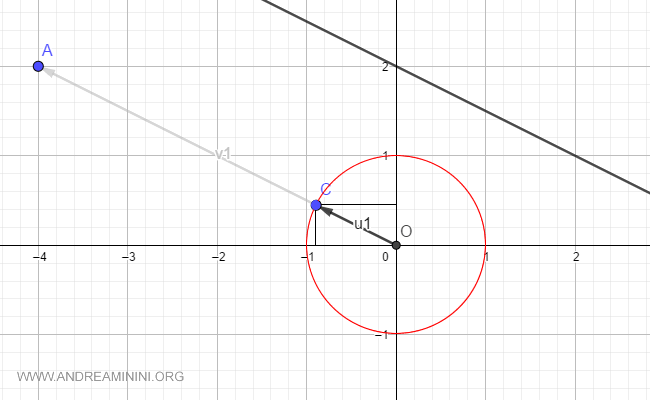
Gli elementi del versore direttore sono i coseni direttori della retta.

$$ u_{r1} = \begin{pmatrix} r_x \\ r_y \end{pmatrix} = \begin{pmatrix} \frac{-4}{ \sqrt{20} } \\ \frac{2}{ \sqrt{20} } \end{pmatrix} $$

Quindi i coseni direttori sono

$$ r_x = \frac{-4}{ \sqrt{20} } = \frac{-4}{ \sqrt{5 \cdot 2^2 } } = \frac{-4}{ 2 \cdot \sqrt{5 } } = \frac{-2}{ \sqrt{5 } } $$

$$ r_y = \frac{2}{ \sqrt{20} } = \frac{2}{ \sqrt{5 \cdot 2^2} } = \frac{2}{ 2 \cdot \sqrt{5 } } = \frac{1}{ \sqrt{5 } } $$

Pertanto

$$ r_x = cos \: \hat{xr} = \frac{-2}{ \sqrt{5 } } $$

$$ r_y = cos \: \hat{yr} = \frac{1}{ \sqrt{5 } } $$

Attenzione. I coseni direttori esprimono la lunghezza del coseno. Non indicano l'ampiezza dell'angolo. Per calcolare l'ampiezza dell'angolo in radianti bisogna calcolare l'arcocoseno ossia la funzione inversa del coseno.

A questo punto calcolo l'arcocoseno ( arccos ) per avere l'ampiezza degli angoli in radianti.

$$ arccos \: r_x = arccos \: \frac{-2}{ \sqrt{5 } } = 2,677 \: rad = 153,43° $$

$$ arccos \: r_y = arccos \: \frac{1}{ \sqrt{5 } } = 1,107 \: rad = 63,43° $$

Dal punto di vista geometrico l'ampiezza dell'angolo r_x comincia con l'asse x e termina con la retta secondo l'orientazione della retta.

Lo stesso vale per l'angolo r_y che va dall'asse y alla retta r.

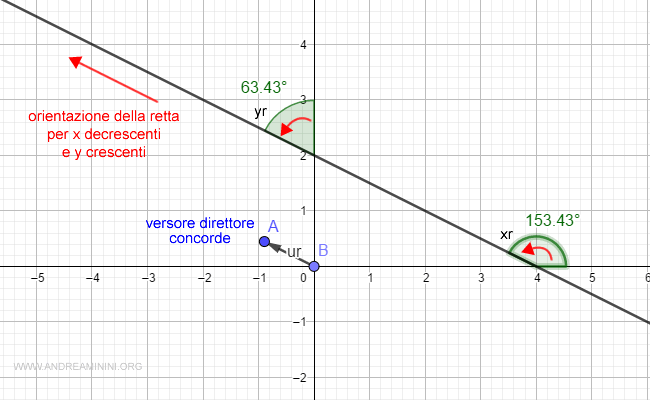
E' se la retta avesse l'orientazione opposta?

In questo caso il vettore concorde è il vettore direttore v₂.

$$ v_{r2} = \begin{pmatrix} 4 \\ -2 \end{pmatrix} $$

Quindi, il versore direttore diventa

$$ u_{r2} = \frac{v_{r2}}{|| v_{r2} ||} $$

$$ u_{r2} = \frac{ \begin{pmatrix} 4 \\ -2 \end{pmatrix} } { \sqrt{20} } = \begin{pmatrix} \frac{4}{ \sqrt{20} } \\ \frac{-2}{ \sqrt{20} } \end{pmatrix} = \begin{pmatrix} \frac{2}{ \sqrt{5} } \\ \frac{-1}{ \sqrt{5} } \end{pmatrix} $$

Pertanto

$$ r_x = cos \: \hat{xr} = \frac{2}{ \sqrt{5 } } $$

$$ r_y = cos \: \hat{yr} = \frac{-1}{ \sqrt{5 } } $$

Per conoscere l'ampiezza degli angoli in radianti calcolo l'arcocoseno ( arccos ).

$$ arccos \: r_x = arccos \: \frac{2}{ \sqrt{5 } } = 0,4636 \: rad = 26,56° $$

$$ arccos \: r_y = arccos \: \frac{-1}{ \sqrt{5 } } 2,034 \: rad = 116,56° $$

Dal punto di vista geometrico l'ampiezza dell'angolo r_x va dall'asse x alla retta secondo l'orientazione della retta.

Lo stesso vale per l'angolo r_y che si estende dall'asse y alla retta.

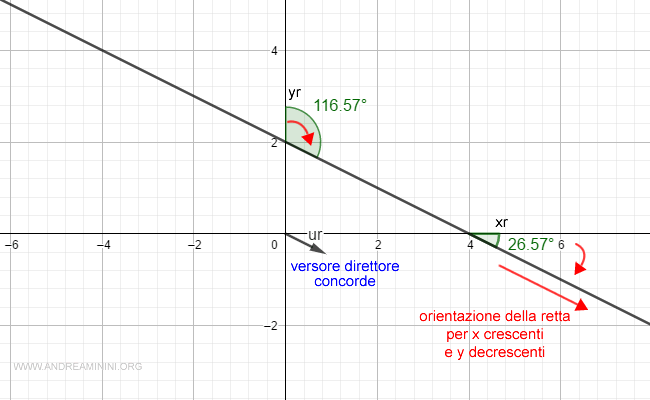
Nota. Cambiando l'orientazione della retta i coseni direttori misurano l'angolo supplementare rispetto all'orientazione precedente. Quindi, se conosco già l'ampiezza degli angoli nel verso opposto, per ottenere i nuovi angoli mi basta calcolare l'angolo supplementare per differenza dall'angolo piatto (π =3.14 rad = 180° ) . In questo modo il calcolo diventa molto più rapido. $$ 180° - 153,43° = 26.56° $$ $$ 180° - 63,43° = 116.56° $$ Osservando il diagramma cartesiano la relazione tra i coseni direttori nelle due orientazioni è subito evidente.

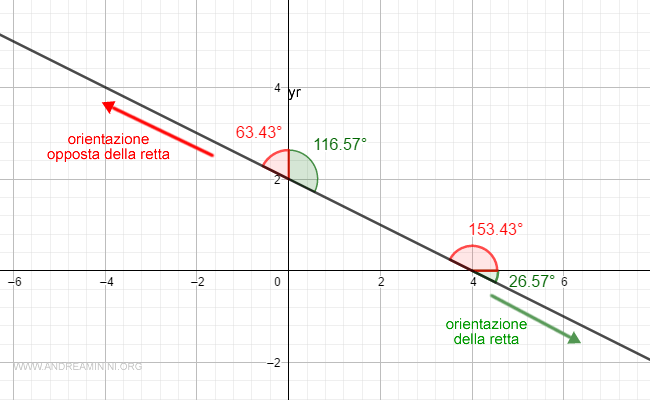
E così via.