Come rappresentare il moto di un punto nello spazio
Posso rappresentare il moto di un punto materiale nello spazio tramite i moti componenti o la traiettoria. Sono due descrizioni matematiche alternative dello stesso fenomeno.
Qual è la differenza tra moti componenti e traiettoria? I moti componenti descrivono le coordinate del punto in ogni istante. La rappresentazione è una successione di punti nello spazio.
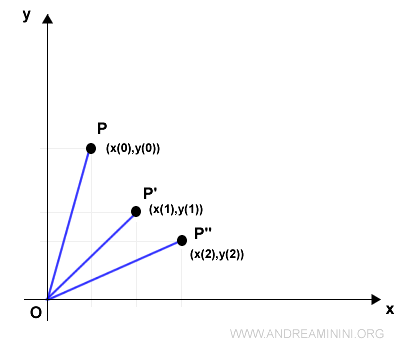
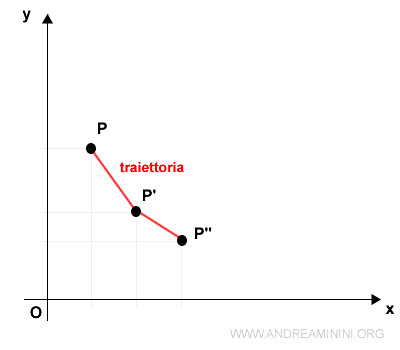
La traiettoria è invece una funzione che descrive lo spostamento del punto dalla posizione iniziale P a quella finale P'' passando per tutti i punti intermedi.
I moti componenti
Il moto di un punto sul piano è individuato con due riferimenti x(t) e y(t) rispetto al sistema di assi cartesiani ortogonali.
In questa rappresentazione il punto di un punto materiale nello spazio è rappresentato in forma vettoriale dal segmento OP che congiunge l'origine con il punto P.
$$ OP = x(t) \cdot i + y(t) \cdot j $$
Dove i e j sono rispettivamente i versori dell'asse delle ascisse e delle ordinate.
Le funzioni x(t) e y(t) invece determinano il valore x e y del punto nel tempo ossia le coordinate cartesiane del punto nello spazio durante il moto.
Per questa ragione sono conosciute come moti componenti
$$ \begin{cases} x(t) \\ y(t) \end{cases} $$
Nello spazio a due dimensioni (piano cartesiano) ci sono due equazioni del moto componente.
Nota. Nello spazio a tre dimensioni le equazioni diventano tre. $$ \begin{cases} x(t) \\ y(t) \\ z(t) \end{cases} $$
I moti componenti descrivono lo spostamento del punto nello spazio.
Esempio
Un esempio di sistema di equazione del moto componente x e y è il seguente
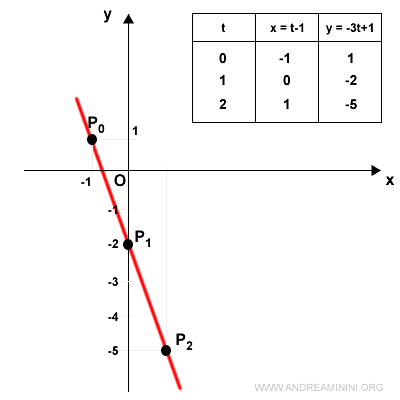
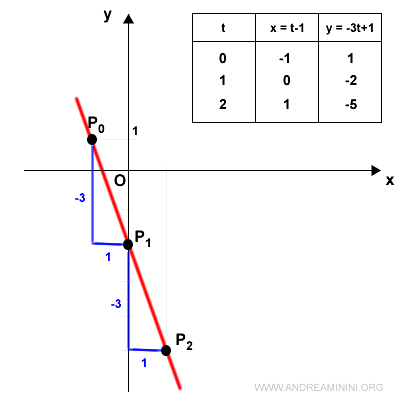
$$ \begin{cases} x(t) = t-1 \\ \\ y(t) = -3t+1 \end{cases} $$
Sostituendo al parametro tempo (t) dei valori da 0 in poi, posso ottenere le coordinate (x,y) dei punti.
Quindi unisco i punti tra loro con dei segmenti per disegnare il grafico.
La rappresentazione con le coordinate polari
In alternativa, la posizione del punto sul piano posso scriverla in termini di coordinati polari del piano r(t) e q(t).
$$ x = r \cos θ $$ $$ y = r \sin θ $$
Dove r è la lunghezza del segmento (raggio) che congiunge il punto P con l'origine O
$$ r = \sqrt{x^2+y^2} $$
oppure
$$ \tan θ = \frac{y}{x} $$
Dal punto di vista grafico
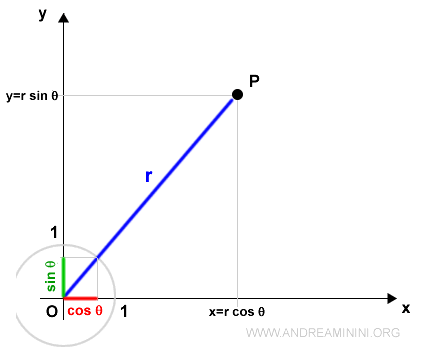
Il segmento OR è anche descritto come raggio vettore.
Il raggio vettore r(t) indica la posizione del punto nel piano in un istante t.
$$ r(t) = OP = x(t) \cdot i + y(t) \cdot j $$
Dove gli scalari i e j sono i versori degli assi cartesiani e sono costanti fisse nel tempo.
Nota. Un versore è un vettore di lunghezza unitaria che indica la direzione, il verso e il modulo (unità di misura) sugli assi. Ogni versore è l'unità di misura dell'asse delle ascisse (i) e delle ordinate (j). Ad esempio, generalmente nel piano cartesiano il versore i è (1,0) e il versore j è (0,1).
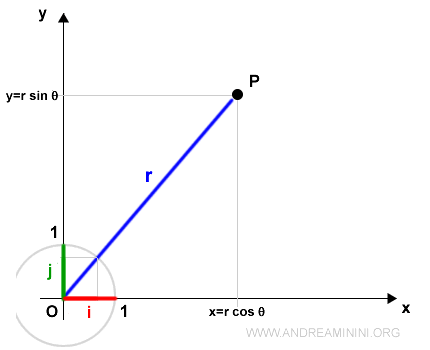
Quindi dalla funzione del raggio vettore r(t) si ottengono le coordinate x(t) e y(t), e viceversa.
La traiettoria
Posso studiare lo spostamento del punto nello spazio anche osservando la sua traiettoria nel tempo.
Cos'è la traiettoria
La traiettoria è l'unione di tutti i punti (x,y) che il punto occupa nel corso del tempo.
Fisso uno di questi punti come punto iniziale P0 , un'unità di misura e calcolo la distanza percorsa dal punto lungo la traiettoria.
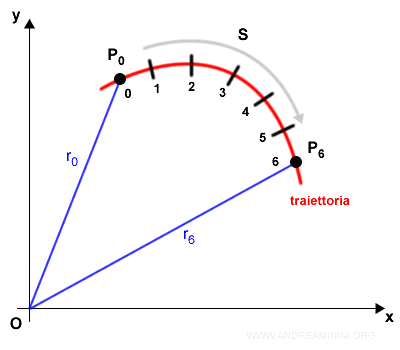
Tutti i punti della traiettoria sono calcolabili tramite un'apposita funzione detta equazione della traiettoria in forma implicita.
$$ f(x,y)=0 $$
Nota. Posso scrivere l'equazione della traiettoria anche in forma esplicita $$ y = f(x) $$
Da sola però l'equazione della traiettoria perché è una dimensione atemporale.
Per descrivere il moto del punto devo considerare anche la dimensione tempo.
All'equazione della traiettoria devo aggiungere l'equazione della legge oraria che misura lo spazio percorso dal punto nel corso del tempo.
$$ S(t) $$
Pertanto, la traiettoria nel tempo è descritta da due equazioni
$$ \begin{cases} f(x,y)=0 \\ S(t) \end{cases} $$
Ora nel diagramma cartesiano c'è sia lo spazio percorso (S) che il tempo (t).
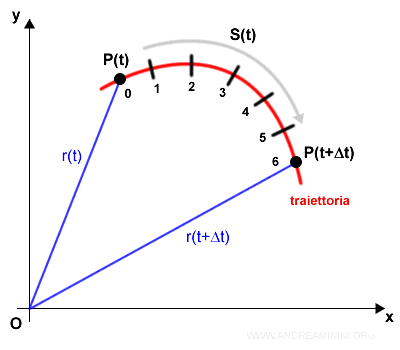
Nota. Nello spazio a tre dimensioni il moto del punto è descritto dall'intersezione di due piani. Quindi, considerando anche la legge oraria, le equazioni del sistema diventano tre. $$ \begin{cases} f(x,y,z)=0 \\ g(x,y,z)=0 \\ S(t) \end{cases} $$
Esempio
Nell'esempio precedente

la traiettoria del punto materiale sul piano è determinata dal seguente sistema
$$ \begin{cases} y(x)=-3x-2 \\ \\ s(t)=s_0+\sqrt{10}(t-t_0) \end{cases} $$
La prima equazione è l'equazione della traiettoria, mentre la seconda è l'equazione della legge oraria.
Nota. C'è una stretta relazione tra il sistema della traiettoria e quello dei moti componenti perché dai moti componenti si ottiene l'equazione della traiettoria per sostituzione. $$ \begin{cases} x(t)=t-1 \\ \\ y(t)=-3t+1 \end{cases} $$ Per eliminare la variabile tempo, metto in evidenza la t nella prima equazione $$ \begin{cases} t=x+1 \\ \\ y=-3t+1 \end{cases} $$ Poi sostituisco la variabile t nella seconda equazione. $$ \begin{cases} t=x+1 \\ \\ y=-3(x+1)+1 \end{cases} $$ e ottengo l'equazione della traiettoria $$ \begin{cases} t=x+1 \\ \\ y=-3x-2 \end{cases} $$ L'equazione della legge orario, invece, la calcolo usando il teorema di Pitagora e la distanza euclidea tra i punti. $$ s(t)=s_0+\sqrt{Δx^2+Δy^2}(t-t_0) $$ Considero s0=0 per semplicità $$ s(t)=\sqrt{1^2+(-3)^2}(t-t_0) $$ $$ s(t)=\sqrt{10}(t-t_0) $$
Come misurare la traiettoria
La lunghezza traiettoria può essere misurata in modo approssimativa tramite il vettore spostamento.
Il vettore spostamento ha il vantaggio d'essere facilmente calcolabile tramite il teorema di Pitagora.
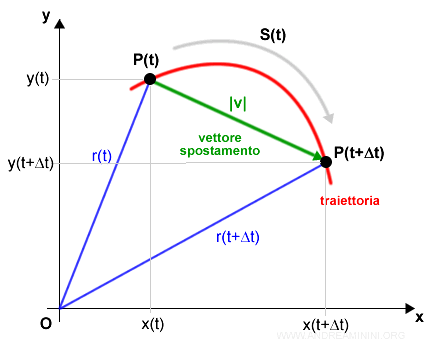
Come si calcola la lunghezza del vettore spostamento. Il vettore spostamento forma un triangolo rettangolo con i raggi vettori e gli assi cartesiani.
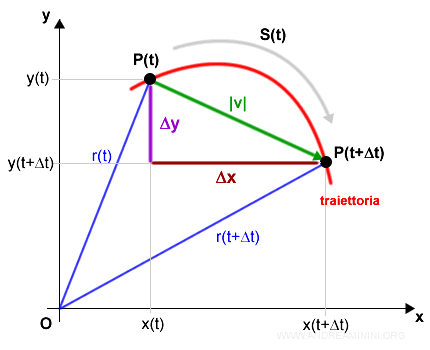
La base del triangolo rettangolo è Δx mentre l'altezza è Δy.
Tuttavia, il vettore spostamento è troppo approssimativo perché S(t)>|v| e in alcuni casi |v| diventa fuorviante.
Come si risolve il problema?
Per ridurre la differenza tra S(t) e |v| posso calcolare le coordinate del punto in un istante temporale intermedio.
In questo modo posso sommare due vettori spostamento |v1|+|v2|
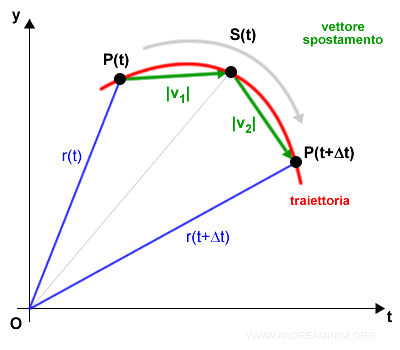
La lunghezza |v1|+|v2| si avvicina molto di più alla lunghezza della traiettoria S(t).
Se considero più istanti temporali la somma degli n vettori spostamento Σ|vn| si avvicina ancora di più alla lunghezza della traiettoria S(t).
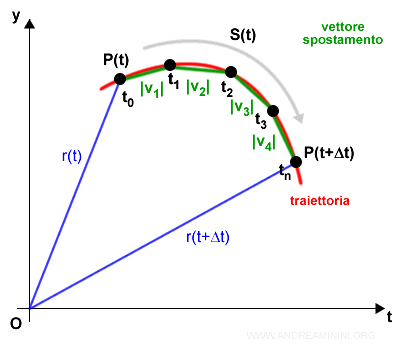
In conclusione, prendendo infiniti istanti di tempo tn la somma Σ|vn| eguaglia la lunghezza della traiettoria S(t).
Si giunge così al calcolo infinitesimale.
E così via.
