La caduta di un grave
In fisica la caduta di un grave è il movimento di un oggetto che cade al suolo per effetto dell'accelerazione di gravità.$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot (t-t_0) \\ x(t) = h + v_0 \cdot (t-t_0) - \frac{1}{2} g \cdot (t-t_0)^2 \end{cases} $$ Dove g è l'accelerazione di gravità, h è l'altezza, t0 è l'istante di tempo iniziale, x0 è la posizione iniziale e v0 è la velocità iniziale di caduta.
Qualsiasi oggetto è soggetto alla forza di gravità.
L'accelerazione di gravità è un vettore costante con modulo g=9,8 m/s2 verso il centro della Terra.
La caduta del corpo è un moto uniformemente accelerato con accelerazione a=-g.
Nota. L'accelerazione di gravità si riduce con l'altezza. Per semplicità considero la forza di gravità al livello del mare. Inoltre, la caduta di un corpo è anche soggetta all'attrito dell'aria che in questa pagina non considero per semplificare i calcoli.
Un esempio pratico
Un oggetto si trova in stato di quiete a un altezza x0=0. Ad esempio, è su un tavolo.
L'altezza h=x0 è la posizione iniziale del corpo.
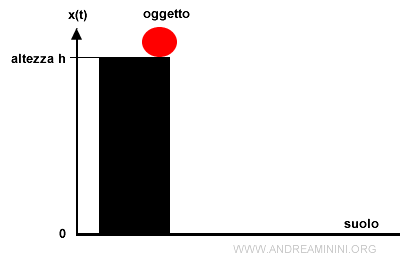
Essendo fermo, l'oggetto ha una velocità iniziale nulla v0=0.
Nell'istante t0=0 spingo l'oggetto verso il bordo del tavolo facendolo cadere.
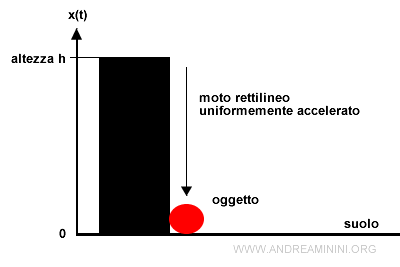
Ora l'oggetto cade in moto rettilineo verso il centro della Terra per effetto della forza di gravità.
Nella caduta l'oggetto segue un moto rettilineo uniformemente accelerato.
Nota. Si tratta di un moto rettilineo perché l'oggetto si sposta su una retta, l'asse verticale x(t), ed è uniformemente accelerato perché l'accelerazione è uguale all'accelerazione gravitazionale (g=9.8 m/s2)
Le formule del moto rettilineo uniformemente accelerato sono le seguenti:
Accelerazione
$$ a(t) = a_0 $$
Velocità
$$ v(t) = v_0 + a(t-t_0) $$
Posizione (legge oraria)
$$ x(t) = x_0 + v_0 (t-t_0) + \frac{1}{2} a(t-t_0)^2 $$
Per semplicità le dispongo in un sistema di equazioni
$$ \begin{cases} a(t) = a_0 \\ v(t) = v_0 + a(t-t_0) \\ x(t) = x_0 + v_0 (t-t_0) + \frac{1}{2} a(t-t_0)^2 \end{cases} $$
In questo caso l'accelerazione è una costante pari all'accelerazione di gravità a=-g=-9,8 m/s2
$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot (t-t_0) \\ x(t) = x_0 + v_0 \cdot (t-t_0) - \frac{1}{2} g \cdot (t-t_0)^2 \end{cases} $$
La posizione iniziale del corpo è x0=h pari all'altezza.
$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot (t-t_0) \\ x(t) = h + v_0 \cdot (t-t_0) - \frac{1}{2} g \cdot (t-t_0)^2 \end{cases} $$
L'istante iniziale in cui cade il corpo è t0=0.
$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot t \\ x(t) = h + v_0 \cdot t - \frac{1}{2} g \cdot t^2 \end{cases} $$
La velocità iniziale del corpo è nulla perché si trova in stato di quiete v0=0.
$$ \begin{cases} a(t) = -g \\ v(t) = - gt \\ x(t) = h- \frac{1}{2}gt^2 \end{cases} $$
Il moto del corpo in caduta si arresta quando tocca il suolo x(t)=0.
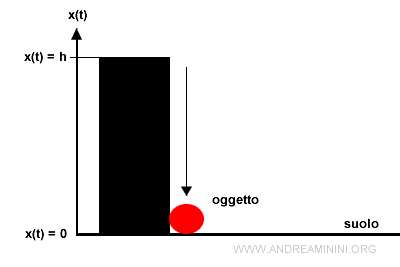
Pertanto, per calcolare il tempo di caduta tc devo trovare la soluzione dell'equazione
$$ x(t) = 0 $$
Dove x(t) è la legge oraria del moto
$$ h- \frac{1}{2}gt^2 = 0 $$
Metto in evidenza t
$$ t^2 = \frac{2 h}{g} $$
Applico la radice quadrata a entrambi i membri
$$ \sqrt{ t^2 } = \sqrt{ \frac{2 h}{g} } $$
$$ t = \sqrt{ \frac{2 h}{g} } $$
Ho così trovato la formula del tempo di caduta tc.
$$ t_c = \sqrt{ \frac{2 h}{g} } $$
Nota. La radice quadrata ha due soluzioni. Una positiva e l'altra negativa. In questo caso va considerato l'istante di tempo positivo (nel futuro) in quanto h>0 e g>0.
Per trovare la velocità d'impatto al suolo, mi basta sostituire il tempo di caduta nell'equazione della velocità.
$$ v(t) = - gt $$
$$ v(t_c) = - gt_c $$
$$ v(t_c) = - g \cdot \sqrt{ \frac{2 h}{g} } $$
$$ v(t_c) = - \sqrt{ \frac{2h}{g} \cdot g^2 } $$
$$ v(t_c) = - \sqrt{ 2gh } $$
Il lancio di un sasso verso l'alto
Cosa accade se lancio un sasso verso l'alto?
Dando per scontato che mi scansi subito dopo per evitare che mi cada in testa... il sasso raggiunge un'altezza massima xm per poi ricadere al suolo.
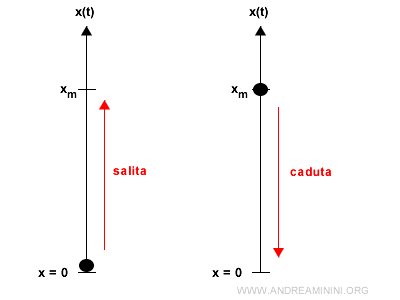
Il fenomeno può sembrare banale ma non lo è, perché il sasso si muove con velocità diverse nel corso del tempo e a un certo punto inverte il verso del suo moto.
Per analizzare questo fenomeno uso le formule del moto uniformemente accelerato
$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot (t-t_0) \\ x(t) = h + v_0 \cdot (t-t_0) - \frac{1}{2} g \cdot (t-t_0)^2 \end{cases} $$
Per semplicità considero l'istante iniziale del lancio t0=0 e la posizione iniziale h=0 ossia x0=0.
Ad esempio, lancio il sasso verso l'alto al livello del mare. In questo modo le formule si semplificano.
$$ \begin{cases} a(t) = -g \\ v(t) = v_0 - g \cdot t \\ x(t) = v_0 \cdot t - \frac{1}{2} g \cdot t^2 \end{cases} $$
Ora lancio il sasso verso l'alto con una velocità iniziale v0>0.
La velocità ha segno positivo perché il verso del moto è concorde con quello dell'asse.
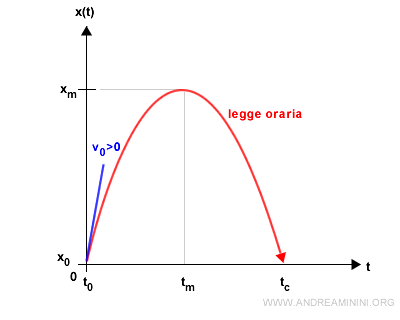
Nota. Questo grafico mostra la legge oraria del moto ossia la relazione tra la posizione x(t) del sasso e il tempo t. Non va confuso con il moto del sasso che è sempre rettilineo.
Nella legge del moto x(t) una forza spinge il sasso verso l'alto mentre un'altra lo attira al suolo.
$$ x(t) = v_0 \cdot t - \frac{1}{2} g \cdot t^2 $$
Man mano che il sasso si muove verso l'alto (v0t) viene attratto in basso dalla forza di gravità terrestre (-1/2 gt2).
L'accelerazione di gravità (-1/2 gt2) cresce in modo quadratico rispetto al tempo mentre la forza (v0t) è lineare.
Quindi, col passare del tempo il moto del sasso verso l'alto rallenta.
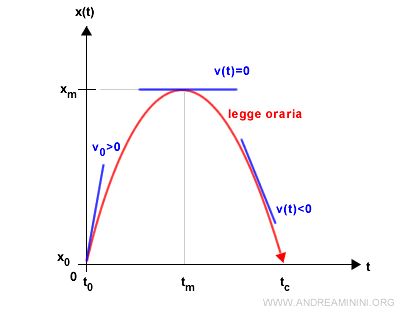
Quando le due forze si eguagliano v0t=1/2 gt2 il moto si arresta e per un istante di tempo il sasso resta sospeso a velocità nulla v(t)=0.
Poi, nell'istante successivo il moto si inverte v0t<1/2 gt2 e il sasso cade verso il suolo.
Quando il sasso tocca il suolo la sua posizione è x(t)=0.
$$ x(t) = 0 $$
Qual è l'altezza massima raggiunta dal sasso?
Per trovare l'altezza massima xm(t) raggiunta dal sasso devo trovare il punto in cui la velocità è nulla.
$$ v(t)=0 $$
Sapendo che la formula della velocità del moto uniformemente accelerato è v(t) = v0-gt
$$ v_0 - g \cdot t = 0 $$
Metto in evidenza il tempo t per trovare l'istante in cui il sasso raggiunge l'altezza massima tm.
$$ t_m = \frac{v_0}{g} $$
Una volta noto l'istante in cui il sasso raggiunge la massima altezza, sostituisco tm nella legge del moto per trovare l'altezza massima xm.
$$ x(t) = v_0 \cdot t - \frac{1}{2} g \cdot t^2 $$
$$ x_m(t) = v_0 \cdot t_m - \frac{1}{2} g \cdot t_m^2 $$
$$ x_m(t) = v_0 \cdot ( \frac{v_0}{g} ) - \frac{1}{2} g \cdot ( \frac{v_0}{g} )^2 $$
$$ x_m(t) = \frac{v_0^2}{g} - \frac{1}{2} ( \frac{v_0^2}{g} ) $$
$$ x_m(t) = \frac{1}{2} ( \frac{v_0^2}{g} ) $$
In questo modo ho trovato l'altezza massima xm raggiunta dal sasso.
$$ x_m(t) = \frac{v_0^2}{2g} $$
Quando il sasso cade al suolo?
Quando il sasso tocca il suolo la legge oraria x(t)=0 è nulla.
$$ x(t) = v_0 \cdot t - \frac{1}{2} g \cdot t^2 = 0 $$
Per trovare l'istante di impatto del sasso al suolo, devo risolvere l'equazione
$$ v_0 \cdot t - \frac{1}{2} g \cdot t^2 = 0 $$
Metto in evidenza il tempo
$$ t \cdot (v_0 - \frac{1}{2} g \cdot t) = 0 $$
Questa equazione ha due soluzioni
$$ \begin{cases} t=0 \\ v_0 - \frac{1}{2} g \cdot t = 0 \end{cases}$$
La prima soluzione è banale. Quando t=0 l'equazione è nulla.
Tuttavia, questa soluzione non mi interessa perché individua l'istante iniziale in cui lancio il sasso.
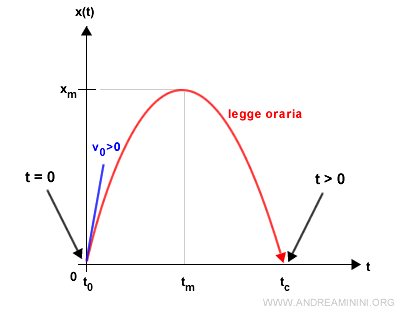
La seconda soluzione è invece quella dell'impatto.
Metto in evidenza t.
$$ v_0 - \frac{1}{2} g \cdot t = 0 $$
$$ - \frac{1}{2} g \cdot t = -v_0 $$
$$ t_c = \frac{2v_0}{g} $$
Ho così trovato l'istante di tempo in cui il sasso cade al suolo (tc).
Qual è la velocità di impatto al suolo?
La formula della velocità del moto uniformemente accelerato è
$$ v(t) = v_0 - g \cdot t $$
Una volta noto l'istante dell'impatto al suolo tc, mi basta sostituirlo nella formula della velocità v(t) per trovare la velocità di impatto.
$$ v(t_c) = v_0 - g \cdot ( \frac{2v_0}{g} ) $$
$$ v(t_c) = v_0 - 2v_0 $$
$$ v(t_c) = -v_0 $$
La velocità di impatto è opposta alla velocità iniziale (v0).
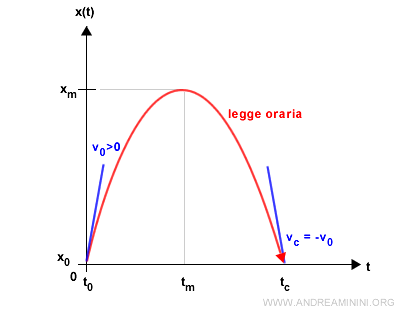
Nota. Questo accade perché il lancio e l'impatto avvengono alla stessa posizione x(0)=x(tc)=h=0. Se lanciassi il sasso da una posizione più alta rispetto al suolo la velocità d'impatto sarebbe maggiore e viceversa.
E così via.
