Cifrari affini
I cifrari affini sono un sistema di cifratura a sostituzione che utilizza l'aritmetica modulare per trasformare le lettere di un messaggio.
La loro caratteristica principale è che applicano una trasformazione affine (lineare) a ciascun carattere del testo in chiaro per produrre il testo cifrato.
Questi cifrari si chiamano "affini" per la funzione matematica usata nella cifratura.
In matematica una funzione affine è una funzione composta da una trasformazione lineare (moltiplicazione) seguita da una traslazione (addizione). In altre parole, una funzione affine ha la forma generale del tipo: $$ f(x)=ax+b $$ Dove a e b sono costanti e la costante "a" è diversa da zero.
La cifratura
La formula di cifratura per un cifrario affine è:
$$ C \equiv (aP + b) \mod m $$
Dove:
- C è il testo cifrato che si ottiene dopo la cifratura.
- P è il testo in chiaro (plaintext) forma numerica dove ogni carattere è associato a un codice numerico (es. A=0, B=1, C=2, ecc.).
- I coefficienti "a" e "b" sono le chiavi del cifrario, che devono essere scelte in modo specifico per cifrare il messaggio.
- La chiave "a" è detta chiave del cifrario (o chiave moltiplicativa). Deve essere un valore co-primo della dimensione dell'alfabeto ossia di "m".
- La chiave "b" è detta chiave dello spostamento (o chiave additiva).
- "m" è la dimensione dell'alfabeto utilizzato. Se utilizzo l'alfabeto inglese è m = 26, ovvero il numero delle lettere maiuscole da A a Z).
La decifratura
La decifratura avviene utilizzando la formula inversa:
$$ P \equiv a' (C - b) \mod m $$
Dove \( a' \) è l'inverso moltiplicativo di \( a \) modulo \( m \) mentre C è il codice numerico di una lettera del testo cifrato.
Quindi, per funzionare correttamente, la chiave di cifratura \( a \) deve essere scelta in modo che abbia un inverso moltiplicativo modulo \( m \).
Per questa ragione i valori \( a \) e \( m \) devono essere interi co-primi, cioè non devono avere altri divisori comuni ad eccezione di 1.
Nota. Anche il cifrario di Cesare può essere considerato come un caso particolare di cifrario affine dove \( a = 1 \) mentre \( b \) rappresenta la quantità di spostamento (shift) per ciascuna lettera. Complessivamente i cifrari affini sono metodo di cifratura a sostituzione più complesso rispetto al semplice cifrario di Cesare. Tuttavia, anche i messaggi codificati con i cifrari affini, se intercettati, sono vulnerabili alla decifratura. Ad esempio, sono decifrabili attraverso l'analisi delle frequenze.
Un esempio pratico
Ecco un esempio pratico usando l'alfabeto inglese composto da m = 26 lettere.
Scelgo come chiave di cifratura a=5 e come chiave di spostamento b=8.
Per prima cosa mi assicuro che la chiave del cifrario "a" e 26 siano coprimi. Il che è vero perché il massimo comun divisore (MCD) di 5 e 26 è 1.
$$ MCD(5,26)=1 $$
Come cifrare una lettera
Per cifrare, uso la formula
$$ C(P) \equiv (a \cdot P + b) \mod m $$
Le lettere dell'alfabeto sono m=26
$$ C(P) \equiv (a \cdot P + b) \mod 26 $$
Supponiamo di voler cifrare la lettera 'A', che ha come valore numerico 0.
Quindi, il codice numerico della lettera è P=0
$$ C(0) \equiv (a \cdot 0 + b) \mod 26 $$
Nota. Il codice numerico assegnato alle lettere può anche variare. In genere, negli esempi didattici si assegna ad 'A' il valore 0, 'B' il valore 1, e così via fino a 'Z' che ha valore 25. In un programma informatico, invece, si usa il codice Ascii/Unicode, dove il carattere "A" è assegnato al valore 65, il carattere "B" a 66, e via dicendo. In ogni caso non cambia nulla.
Sostituisco le chiavi a=5 e b=8 nella formula di cifratura.
$$ C(0) \equiv (5 \cdot 0 + 8) \mod 26 $$
$$ C(0) \equiv 8 \mod 26 $$
A questo punto devo risolvere la congruenza modulare.
La divisione 8:26 ha resto 8, perché il ventisei sta nell'otto zero volte con resto uguale a otto.
Quindi, la congruenza vale 8.
$$ C(0) \equiv 8 $$
Il codice numerico 8 è associato alla nona lettera del'alfabeto inglese ovvero alla lettera "I".
E' la nona lettera (anziché l'ottava) perché si inizia a contare da zero con A=0, B=1, C=2, D=3, E=4, F=5, G=6, H=7, I=8.
Quindi, la lettera in chiaro 'A' (codice numerico zero) viene cifrata come 'I'.
Come decifrare una lettera
Per decifrare, devo prima calcolare l'inverso moltiplicativo della chiave di cifratura a=5
L'inverso moltiplicativo è quel valore (a') che moltiplicato per il valore "a" è uguale a 1 nella moltiplicazione modulo 26.
Per trovarlo devo risolvere un'altra congruenza nel modulo 26.
$$ a \cdot a' \equiv 1 \ \mod 26 $$
Dove a=5
$$ 5 \cdot a' \equiv 1 \ \mod 26 $$
Per a=5, l'inverso è a′=21 perché 5⋅21=105 e la divisione 105:26 dà come resto 1.
$$ 5 \cdot 21 \equiv 1 \ \mod 26 $$
Una volta ottenuto l'inverso moltiplicativo, posso usarlo nella formula di decifratura per qualsiasi carattere.
$$ D(C) \equiv a' (C - b) \mod m $$
$$ D(C) \equiv 21 \cdot (C - b) \mod m $$
Le lettere dell'alfabeto sono sempre m=26 e la chiave di spostamento che ho scelto per cifrare il messaggio è b=8.
$$ D(C) \equiv 21 \cdot (C - 8) \mod 26 $$
Provo a decifrare la lettera cifrata "I" che ha valore numerico C=8
$$ D(8) \equiv 21 \cdot (8 - 8) \mod 26 $$
$$ D(8) \equiv 21 \cdot 0 \mod 26 $$
$$ D(8) \equiv 0 \mod 26 $$
Il risultato è 0 perché la divisione 0:26 ha resto 0, ovvero lo zero sta nel ventisei zero volte, con resto zero.
$$ D(8) \equiv 0 $$
Il risultato 0 corrisponde al codice numerico della lettera 'A' nell'alfabeto.
Quindi, la lettera 'A' cifrata con chiave a=5 e b=8 diventa 'I', e la 'I' decifrata con l'inverso a′=21 e b=8 ritorna ad essere 'A'.
Esempio 2
Considero a=5 e b=8. Il numero a=5 è coprimo con 26, quindi è una scelta valida per a.
$$ MCD(5,26)=1 $$
Il numero delle lettere dell'alfabeto inglese è sempre lo stesso, ovvero m=26.
Una volta scelta la chiave di cifratura (a) e quella di spostamento (b) posso procedere con la cifratura.
Come cifrare una lettera
Per cifrare la lettera "C" che ha valore numerico 2 nell'alfabeto inglese scrivo:
$$ C(P) \equiv (a \cdot P + b) \mod m $$
In questo caso a=5, b=8, m=26
$$ C(P) \equiv (5 \cdot P + 8) \mod 26 $$
La lettera da cifrare è la lettera C a cui corrisponde il codice numerico 2 nell'alfabeto inglese (A=0, B=1, C=2, ... )
Quindi P=2
$$ C(2)=(5 \cdot 2+8) \ mod \ 26 $$
$$ C(2)=(10+8) \ mod \ 26 $$
$$ C(2)=18 \ mod \ 26 $$
A questo punto risolvo la congruenza modulo 26.
Il risultato è 18 perché la divisione 18:26 ha resto zero, ovvero il ventisei sta nel diciotto zero volte con resto diciotto.
$$ C(2)=18 $$
Quindi, il codice cirrato della lettara "C" è la lettera dell'alfabeto che ha il codice numerico 18.
Il valore numerico 18 corrisponde alla lettera "S" nell'alfabeto inglese. Quindi, "C" viene cifrato come "S".
Come decifrare una lettera
Per decifrare la lettera "S":
Per prima cosa devo trovare l'inverso moltiplicativo di 5 modulo 26.
Questo è 21, poiché 5×21=105 e 105 mod 26=1.
$$ D(18)=21 \cdot (18−8) \ mod \ 26 $$
$$ D(18)=21 \cdot 10 \ mod \ 26 $$
$$ D(18)=210 \ mod \ 26 $$
In questo caso il risultato è 2 perché la divisione 210:26 ha resto 2, ovvero il ventisei sta nel duecentodieci otto volte con resto due.
$$ D(18)=2 $$
Quindi, la lettera decifrata "S" corrisponde a quella con il codice numerico 2 ovvero alla lettera "C".
Nota. Per verificare il risultato ho realizzato un semplice tool online sulla cifratura affine. Basta inserire la lettera da cifrare/decifrare, la chiave di cifratura e di spostamento, per ottenere in tempo reale il carattere equivalente cifrato o decifrato. Può essere utile per esercitarsi.
Osservazioni
Alcune osservazioni e note a margine
- In un cifrario affine i valori delle chiavi "a" e "b" sono compresi tra 1 e 25
- Per la chiave di cifratura "a" il valore deve essere scelto tra i numeri che sono coprimi con 26, dato che ci sono 26 lettere nell'alfabeto inglese. Un numero è coprimo con 26 se il suo massimo comun divisore (MCD) con 26 è 1, ovvero se non ha divisori in comune. Quindi, i possibili valori di "a" sono numeri nell'intervallo da 1 a 25 che soddisfano questa condizione. In particolar modo, i numeri coprimi con 26 sono solo dodici: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 e 25.
- Per la chiave di spostamento "b" il valore può essere qualsiasi intero nell'intervallo da 0 a 25, inclusi entrambi gli estremi. Questo perché la chiave "b" rappresenta un semplice scorrimento all'interno dell'alfabeto e non ha requisiti di coprimalità come la chiave "a". Questi range assicura che ogni lettera possa essere cifrata e poi decifrata in modo univoco, mantenendo la funzione di cifratura invertibile.
- L'alfabeto inglese genera 312 sistemi di cifratura affine
L'alfabeto inglese è composto da 26 lettere. La chiave di cifratura "a" può assumere solo valori coprimi con 26 che, in questo caso, sono solo 12 valori possibili.Usando la funzione di Eulero φ(26) posso conoscere anche quali sono: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 e 25. Tutti questi valori non hanno divisori in comune con ventisei, ovvero sono coprimi con ventisei.
La chiave di spostamento "b", invece, può assumere un valore qualsiasi da 0 a 25 nell'aritmetica modulo 26 e non occorre che sia coprimo con ventisei, quindi può assumere 26 valori in tutto. Riepilogando, ho 12 scelte per la chiave "a" e 26 scelte possibili per la chiave "b". $$ 12 \cdot 26 = 312 $$ Pertanto, complessivamente ci sono 312 combinazioni di cifrari affini possibili usando l'alfabeto inglese con 26 lettere maiuscole. - Programma del cifrario affine in Python
Ho realizzato un piccolo programma in linguaggio Python per codificare e decodificare un testo usando il sistema di cifratura affine sull'alfabeto inglese. - I cifrari affini sono poco sicuri perché facilmente decifrabili se intercettati
La sicurezza di un messaggio cifrato mediante un cifrario affine è relativamente bassa poiché è possibile decifrarlo senza necessariamente conoscere le chiavi "a" e "b". Del resto le combinazioni possibili di cifratura sono solo 312 con l'alfabeto inglese (26 lettere maiuscole). Ma anche senza analizzare tutte le combinazioni, la vulnerabilità del cifrario è dovuta all'analisi delle frequenze, una tecnica che sfrutta la distribuzione non uniforme delle lettere in una lingua. Identificando le lettere che appaiono con maggiore o minore frequenza, posso fare delle ipotesi sulle corrispondenze tra le lettere del testo cifrato e del testo in chiaro. Per calcolare le chiavi di cifratura "a" e di traslazione "b", è sufficiente identificare correttamente almeno due lettere del testo cifrato.Esempio. Considero un testo cifrato con le chiavi a=5 e b=8 sull'alfabeto inglese composto da m=26 lettere. Il corpus del testo cifrato è composto da migliaia di parole e questo mi permette di analizzare la frequenza di ogni lettera. Ecco un esempio di codifica sulla parola "ABACO" che diventa "INISA".
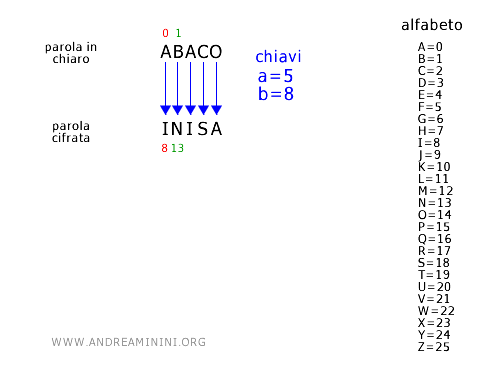
Dopo l'analisi delle frequenze delle lettere nel testo mi accorgo che la frequenza della lettera "I" (codice 8) nel testo cifrato è simile alla frequenza della "A" (codice 0) nei testi scritti in italiano. Inoltre, la frequenza della lettera "N" (codice 13) nel testo cifrato è simile a quella della lettera "B" (codice 1) nei testi in italiano. Quindi, formulo l'ipotesi che la codifica delle due lettere sia "A"→"I" e "B"→"N". Conoscendo la formula della codifica di un sistema affine C = aP + B dove C è il codice della lettera cifrata e P è quello della lettera in chiaro, posso costruire un sistema di equazioni con le congruenze modulari. $$ \begin{cases} 8 \equiv a \cdot 0 + b \ \ mod \ 26 \\ \\ 13 \equiv a \cdot 1 + b \ \ mod \ 26 \end{cases} $$ La prima equazione indica che "I" (codice 8) è una congruenza modulo 26 della lettera "A" (codice 0). La seconda equazione, invece, indica che "N" (codice 13) è una congruenza modulare della lettera "B" (codice 1). A questo punto mi basta risolvere il sistema di equazioni per conoscere le chiavi "a" e "b". In questo caso la soluzione è semplice, perché dalla prima congruenza ottengo già il valore della chiave di spostamento b=8, poiché l'altra chiave è moltiplicata per zero. $$ \begin{cases} 8 \equiv b \ \ mod \ 26 \\ \\ 13 \equiv a + b \ \ mod \ 26 \end{cases} $$ Pertanto, mi basta sostituire b=8 nella seconda congruenza per trovare anche il valore della chiave di cifratura. $$ \begin{cases} 8 \equiv b \ \ mod \ 26 \\ \\ 13 \equiv a + 8 \ \ mod \ 26 \end{cases} $$ Risolvo la seconda congruenza modulare. $$ \begin{cases} 8 \equiv b \ \ mod \ 26 \\ \\ 13 - 8 \equiv a \ \ mod \ 26 \end{cases} $$ E ottengo il valore della chiave di cifratura che in questo caso è a=5. $$ \begin{cases} 8 \equiv b \ \ mod \ 26 \\ \\ 5 \equiv a \ \ mod \ 26 \end{cases} $$ In questo modo ho ottenuto entrambe le chiavi a=5 e b=8 del sistema di cifratura affine. Va detto che questo sistema era veramente molto semplice da risolvere. In generale, per risolvere un qualsiasi sistema di equazioni lineari posso anche trasformarlo in forma vettoriale. $$ \begin{cases} 8 \equiv a \cdot 0 + b \ \ mod \ 26 \\ \\ 13 \equiv a \cdot 1 + b \ \ mod \ 26 \end{cases} $$ $$ \begin{pmatrix} 8 \\ 13 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} a \\ b \end{pmatrix} $$ Dove la matrice che indico con A è la matrice dei coefficienti. $$ \begin{pmatrix} 8 \\ 13 \end{pmatrix} = A \cdot \begin{pmatrix} a \\ b \end{pmatrix} $$ Per conoscere se il sistema ha una soluzione, più soluzioni o nessuna utilizzo il teorema di Rouché-Capelli. Se il sistema ammette soluzioni, procedo con il calcolo. La soluzione del sistema lineare si ottiene calcolando la matrice inversa A-1. $$ A^{-1} \cdot \begin{pmatrix} 8 \\ 13 \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix} $$ Calcolo la matrice inversa A-1 e svolgo la moltiplicazione riga per colonna della matrice per il vettore. $$ \begin{pmatrix} -1 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 8 \\ 13 \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix} $$ $$ \begin{pmatrix} -1 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 8 \cdot (-1) + 13 \cdot (1) \\ 8 \cdot (1) + 13 \cdot (0) \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix} $$ $$ \begin{pmatrix} -8 + 13 \\ 8 + 0 \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix} $$ $$ \begin{pmatrix} 5 \\ 8 \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix} $$ Questo metodo di risoluzione vettoriale mi permette di conoscere le chiavi "a" e "b" del cifrario affine a partire da due lettere anche nei sistemi di equazioni più difficili da risolvere. In questo caso le chiavi sono a=5 e b=8. Ovviamente, la chiave "a" e "m"=26 devono essere numeri interi co-primi. Inoltre, la matrice dei coefficienti deve avere un determinante non nullo, det(A)≠0 per avere una matrice inversa. Inoltre, il determinante della matrice dei coefficienti det(A) è co-primo con "m". Questo perché l'inversa di una matrice esiste se e solo se il determinante è coprimo con "m" nel contesto della crittografia affine.
E così via.
