Teoria cinetica dei gas
La teoria cinetico-molecolare dei gas spiega il comportamento di una sostanza gassosa tramite le proprietà delle particelle del gas.
La teoria cinetica è stata elaborata nella metà del XIX secolo dai fisici Maxwell, Boltzmann e Clausius.
A cosa serve?
Le leggi sui gas ideali sono state scoperte semplicemente tramite l'osservazione sperimentale senza approfondire sulle cause.
Nota. Ad esempio, l'equazione di stato dei gas ideali descrive bene il comportamento dei gas in condizioni ambientali normali ma non spiega le cause della relazione. $$ PV = n RT $$
La teoria cinetica dei gas, invece, spiega le cause del comportamento dei gas tramite l'analisi molecolare del movimento delle particelle che compongono la sostanza gassosa.
In questo modo fornisce una spiegazione fisica ai risultati empirici delle leggi sui gas ideali.
Nella teoria cinetico-molecolare
- La pressione di un gas è causata dalle collisioni delle particelle del gas con il recipiente. Quanto maggiore è la frequenza e la forza degli urti, tanto maggiore è la pressione del gas.
- La temperatura assoluta di un gas è determinata dall'energia cinetica media delle particelle. Quando due gas diversi hanno la stessa temperatura, hanno anche la stessa energia cinetica media.
La velocità media e l'energia cinetica media
Studiare il moto delle particelle con le leggi della meccanica classica è molto difficile, perché in una piccola quantità di gas sono presenti migliaia di particelle.
E' quindi impossibile spiegare il comportamento di ogni singola particella.
Per questo motivo nella teoria cinetica dei gas si ricorre al metodo statistico e ai valori medi. In particolar modo alla velocità media e all'energia cinetica media.
Nota. I valori della velocità media e dell'energia cinetica media non sono esatti, ma sono comunque molto vicini alla velocità e all'energia cinetica più probabile di ogni particella. Pertanto, è una semplificazione teorica accettabile.
L'energia cinetica media (Ec) è pari a
$$ E_c = \frac{1}{2} m \bar{v}^2 $$
Dove v è la velocità media delle particelle e m è la massa delle particelle.
La pressione
La pressione (P) è una forza (F) perpendicolare a una superficie (S).
$$ P=\frac{F}{S} $$
Secondo la legge di Newton la forza è pari alla massa (m) per l'accelerazione (a) ossia F=m*a.
$$ F = m \cdot a $$
A sua volta l'accelerazione è il rapporto tra la velocità (v) e il tempo (t) ossia a=v/t.
$$ F = m \cdot \frac{v}{t} = \frac{mv}{t} $$
Quindi, la forza è uguale alla variazione della quantità di moto (mv).
Per semplicità considero una sola particella in un recipiente cubico con lati di lunghezza l.
La particella si muove sull'asse orizzontale x da una parete A alla parete B, urta sulla parete B e torna indietro fino alla parete A.
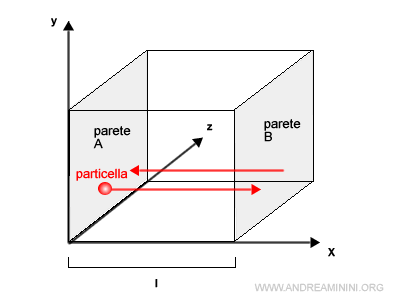
La variazione della quantità di moto (mvx) della particella sull'asse x durante il percorso è pari a
$$ mv_x - m(-v_x) =2 mv_x $$
Nota. Da A a B il moto è m(vx) mentre da B ad A è m(-vx) perché la velocità è opposta. Essendo una variazione, devo calcolare la differenza tra queste quantità di moto. Quindi mvx-(-mvx)=mvx+mvx=2mvx.
La particella percorre una distanza 2l.
Sapendo che la velocità sull'asse x è vx=s/t dove s=2l è lo spazio percorso
$$ v_x = \frac{s}{t} = \frac{2l}{t} $$
se conosco la velocità dello spostamento orizzontale posso calcolare il tempo dello spostamento.
$$ t = \frac{2l}{v_x} $$
Ho ottenuto tutte le componenti della forza ossia mv e t.
Quindi, le sostituisco nella formula della forza.
$$ F = \frac{mv}{t} $$
$$ F = \frac{2 mv_x}{(\frac{2l}{v_x})} $$
$$ F = 2 mv_x \cdot \frac{v_x}{2l} $$
$$ F = mv_x \cdot \frac{v_x}{l} $$
$$ F = \frac{mv_x^2}{l} $$
Una volta ottenuta la formula della forza F la sostituisco nella formula della pressione.
$$ P=\frac{F}{S} $$
$$ P=\frac{\frac{mv_x^2}{l}}{S} $$
Sapendo che la superficie di una parete quadrata con lato l è S=l2
$$ P=\frac{\frac{mv_x^2}{l}}{l^2} $$
$$ P= \frac{mv_x^2}{l} \cdot \frac{1}{l^2} $$
$$ P= \frac{mv_x^2}{l^3} $$
Essendo il recipiente un cubo il valore l3 è il volume del recipiente ossia V=l3
$$ P= \frac{mv_x^2}{V} $$
Poiché sto considerando lo spostamento orizzontale sull'asse x, questa è la pressione Px
$$ P_x= \frac{mv_x^2}{V} $$
Ripeto la stessa operazione considerando gli spostamenti sull'asse y e sull'asse z, ottenendo due formule simili della pressione.
$$ P_y= \frac{mv_y^2}{V} $$
$$ P_z= \frac{mv_z^2}{V} $$
Queste formule calcolano la pressione esercitata dal moto della particella di gas sulle pareti del recipiente cubico rispetto agli assi x, y, z.
Considerando un numero di Avogadro N di particelle di gasnel recipiente le formule della pressione diventano:
$$ P_x= N \cdot \frac{mv_x^2}{V} $$
$$ P_y= N \cdot \frac{mv_y^2}{V} $$
$$ P_z= N \cdot \frac{mv_z^2}{V} $$
C'è però un aspetto ancora da correggere.
Queste formule associano la stessa velocità vx, vy e vz a tutte le N particelle del gas ma questo è poco realistico.
In realtà le N particelle si muovono con velocità diverse.
Non conoscendo la velocità di ogni singola particella di gas, è meglio utilizzare la velocità media delle particelle.
$$ P_x= N \cdot \frac{m \bar{v}_x^2}{V} $$
$$ P_y= N \cdot \frac{m \bar{v}_y^2}{V} $$
$$ P_z= N \cdot \frac{m \bar{v}_z^2}{V} $$
La somma delle velocità vx, vy e vz determina la velocità quadratica media.
$$ \bar{v}^2 = \bar{v}_x^2 + \bar{v}_y^2 + \bar{v}_z^2 $$
Poiché il moto è casuale, posso semplificare considerando le velocità vx, vy e vz uguali a un terzo della quadratica media.
$$ \frac{ \bar{v}^2 }{3} = \bar{v}_x^2 = \bar{v}_y^2 = \bar{v}_z^2 $$
Poi sostituisco i valori di vx, vy e vz nelle formule della pressione con v/3
$$ P_x= N \cdot \frac{m \bar{v}^2}{3V} $$
$$ P_y= N \cdot \frac{m \bar{v}^2}{3V} $$
$$ P_z= N \cdot \frac{m \bar{v}^2}{3V} $$
La pressione sulle pareti rispetto agli assi x, y, z è uguale.
Quindi, in generale la pressione delle particelle su tre pareti del recipiente cubico è pari a
$$ P= N \cdot \frac{m \bar{v}^2}{3V} $$
In questo modo ho trovato la formula della pressione.
L'energia cinetica
L'energia cinetica del movimento di una particella che si muove in un recipiente cubico è pari a
$$ E_{c} = \frac{1}{2} mv^2 $$
Nel caso di N particelle, come per il caso della velocità devo usare i valori i medi di energia cinetica.
$$ \bar{E_{c}} = \frac{1}{2} N m \bar{v}^2 $$
Sapendo che la formula della pressione è la seguente
$$ P= N \cdot \frac{m \bar{v}^2}{3V} $$
si capisce subito che l'energia cinetica è una componente della pressione
$$ P= Nm \bar{v}^2 \cdot \frac{1}{3V} $$
poiché il termine Nmv2 è uguale a due volte l'energia cinetica 2Ec
$$ P= 2E_c \cdot \frac{1}{3V} $$
$$ P= \frac{2E_c}{3V} $$
Spostando il volume V a destra ottengo la legge di Boyle.
$$ PV= \frac{2E_c}{3} $$
Sapendo che la legge di Boyle è
$$ PV = RT $$
ne consegue che il prodotto tra la pressione (P) e il volume (V) a temperatura costante (T) è uguale a
$$ PV = RT = \frac{2E_c}{3} $$
Dove R è la costante universale dei gas.
Quindi, PV è un valore costante pari a 2/3 dell'energia cinetica.
Questo conferma la legge di Boyle.
Il legame tra energia cinetica, velocità e temperatura
Dalla formula dell'energia cinetica
$$ PV = RT = \frac{2E_c}{3} $$
si deduce anche che l'energia cinetica delle particelle è determinata dalla temperatura (T).
$$ E_c = \frac{3RT}{2} $$
Poiché l'energia cinetica è, a sua volta, legata alla velocità delle particelle, anche la velocità delle particelle è determinata dalla temperatura (T).
E questo conferma teoricamente un altro risultato sperimentale sui gas.
Quanto più aumenta la temperatura, tanto più aumenta la velocità e l'energia cinetica delle particelle del gas. E viceversa.
La legge di Graham
Sapendo che l'energia cinetica media è uguale a 1/2 Nmv2 e a 3RT/2
$$ E_c = \frac{1}{2}Nmv^2 $$
$$ E_c = \frac{3RT}{2} $$
Se N è il numero di Avogadro (numero di particelle) e m è la massa della particella del gas, allora N·m è il peso molecolare M del gas.
Quindi posso sostituire Nm con M.
$$ E_c = \frac{1}{2}Mv^2 $$
$$ E_c = \frac{3RT}{2} $$
Pertanto, le due formule sono uguali
$$ \frac{1}{2}Mv^2 = \frac{3RT}{2} $$
Ne deduco che se la temperatura T è costante anche la velocità quadratica media v2 del gas è costante, poiché il peso molecolare M e la costante universale dei gas R sono costanti.
E ovviamente, anche l'energia cinetica media (Ec) è costante.
Se considero due gas A e B a temperatura costante T, questi hanno un peso molecolare diverso MA e MB ma la stessa energia cinetica Ec perché la temperatura T è la stessa.
$$ E_c = \frac{1}{2}M_Av_A^2 $$
$$ E_c = \frac{1}{2}M_Bv_B^2 $$
Quindi posso scrivere
$$ \frac{1}{2}M_Av_A^2 = \frac{1}{2}M_Bv_B^2 $$
Con un semplici passaggi algebrici sposto le velocità quadratiche medie a sinistra e i pesi molecolari a destra
$$ \frac{v_A^2}{v_B^2} = \frac{ \frac{1}{2}M_B }{ \frac{1}{2}M_A } $$
Semplifico eliminando 1/2 a numeratore e denominatore nel membro di destra
$$ \frac{v_A^2}{v_B^2} = \frac{ M_B }{ M_A } $$
Poi metto entrambi i membri dell'equazione sotto radice quadrata
$$ \sqrt{ \frac{v_A^2}{v_B^2} } = \sqrt{ \frac{ M_B }{ M_A } } $$
$$ \frac{ \sqrt{ v_A^2 } }{ \sqrt{ v_B^2 } } = \frac{ \sqrt{ M_B } }{ \sqrt{ M_A } } $$
$$ \frac{ v_A }{ v_B } = \frac{ \sqrt{ M_B } }{ \sqrt{ M_A } } $$
In questo modo ho ottenuto la formula della legge di Graham.
Il principio di Avogadro
Considero l'energia cinetica di due gas diversi A e B con NA e NB particelle a parità di temperatura, pressione e volume.
Le particelle hanno rispettivamente massa mA e mB.
A parità di temperatura i gas A e B hanno la stessa energia cinetica.
$$ E_{c} = \frac{1}{2}N_A m_A v^2_A $$
$$ E_{c} = \frac{1}{2}N_B m_B v^2_B $$
Pertanto, posso scrivere l'equazione
$$ \frac{1}{2}N_A m_A v^2_A = \frac{1}{2}N_B m_B v^2_B $$
Considerando una singola particella per gas l'energia cinetica dei gas è uguale a
$$ E_{c} = \frac{1}{2}m_A v^2_A $$
$$ E_{c} = \frac{1}{2}m_B v^2_B $$
Quindi, i due membri di destra sono uguali
$$ \frac{1}{2}m_A v^2_A = \frac{1}{2}m_B v^2_B $$
Pertanto, tornando alla precedente
$$ \frac{1}{2}N_A m_A v^2_A = \frac{1}{2}N_B m_B v^2_B $$
I termini (mAv2A)/2 e (mBv2B)/2 sono uguali è posso sostituirli con un valore K
$$ N_A K = N_B K $$
Poi semplifico eliminando K da entrambi i membri
$$ N_A = N_B $$
Quindi, due volumi di gas diversi a parità di temperatura e pressione hanno lo stesso numero di particelle (NA=NB).
E questo conferma il principio di Avogadro.
E così via.
