Insieme limitato
Cos'è un insieme limitato
Un insieme è limitato se esiste almeno un numero reale M tale che ogni elemento dell'insieme è compreso tra -M e +M. $$ - M \le a \le +M \:\:\: \forall \: a \in A $$ ossia $$ | a | \le M \:\:\: \forall \: a \in A $$
Un insieme limitato è anche limitato inferiormente e limitato superiormente
La dimostrazione
A] Se vale la disequazione
$$ | a | \le M \:\:\: \forall \: a \in A $$
allora per la proprietà del valore assoluto si ha
$$ -M \le a \le M \:\:\: \forall \: a \in A $$
Allora basta considerare -M come limite inferiore e +M come limite superiore.
B] Se vale la seguente disequazione dove l e L sono due numeri reali
$$ l \le a \le L \:\:\: \forall \: a \in A $$
allora basta prendere il valore massimo tra l e L
$$ M = max(|l|,|L|) $$
e usare la disequazione
$$ | a | \le M \:\:\: \forall \: a \in A $$
per soddisfare la relazione
$$ -M \le l \le a \le L \le M \:\:\: \forall a \in A $$
Un esempio pratico
Ho l'insieme reale A composto da sette elementi
$$ A = \{ -7, 4, 2, 6, 3, 5, 1 \} $$
L'insieme ha infiniti minoranti nell'intervallo (-∞, -7] dei numeri reali e infiniti maggioranti nell'intervallo [6,+∞) dei numeri reali.
Prendo in considerazione soltanto il minorante più alto l=-7 e il maggiorante più basso L=6.
$$ l = -1 \\ L = 6 $$
Poi calcolo il valore massimo (max) tra il valore assoluto del minorante l e del maggiorante L.
$$ M = max(l, L) $$
$$ M = max( |-7|, |6|) $$
$$ M = max(7, 6) $$
$$ M = 7 $$
Quindi, esiste un numero reale M=7 tale che
$$ -M \le a \le M \:\:\: \forall a \in A $$
$$ -7 \le a \le 7 \:\:\: \forall a \in A $$
La condizione di limitatezza dell'insieme è soddisfatta.
Pertanto, l'insieme A è un insieme limitato
Insieme limitato inferiormente
Un insieme è limitato inferiormente se esiste almeno un numero reale M tale ogni elemento dell'insieme è maggiore uguale di M. $$ a \ge M \:\:\: \forall \: a \in A $$
Un insieme limitato inferiormente ha almeno un elemento minorante.
Se un insieme è limitato inferiormente ha sempre un numero finito come estremo inferiore.
In un insieme limitato di numeri reali, non vuoto, l'estremo inferiore è il massimo dei minoranti.
$$ m = inf (A) = \begin{cases} m \le a \:\:\: \forall a \in A \\ \\ \forall ε>0 \: \exists \: a \in A \: : \: m+ε>a \end{cases} $$
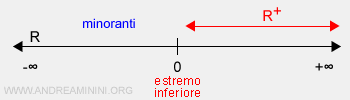
Esempio. L'insieme dei numeri reali positivi R+ è un insieme limitato inferiormente perché i suoi elementi sono compresi nell'intervallo (0,+∞). L'insieme è limitato inferiormente con M=0, dove M=0 è il minorante più alto (estremo inferiore). E' invece illimitato superiormente perché non esiste alcun maggiorante e l'estremo superiore è +∞.
Se l'insieme non è limitato inferiormente, l'estremo inferiore è meno infinito (-∞).
$$ inf(A) = -∞ \Leftrightarrow \forall \:l\: \in R\: \exists\: a \in A\: : \:a < l $$
Insieme limitato superiormente
Un insieme è limitato superiormente se esiste almeno un numero reale M tale ogni elemento dell'insieme è minore-uguale a M. $$ a \le M \:\:\: \forall \: a \in A $$
Un insieme limitato superiormente ha almeno un elemento maggiorante.
Se un insieme è limitato superiormente ha sempre un numero finito come estremo superiore.
In un insieme limitato di numeri reali, non vuoto, l'estremo superiore è il minimo dei maggioranti.
$$ M = sup (A) = \begin{cases} M \ge a \:\:\: \forall a \in A \\ \\ \forall \: ε>0 \: \exists \: a \in A \: : \: M-ε<a \end{cases} $$
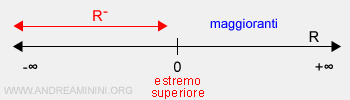
Esempio. L'insieme dei numeri reali negativi R- è un insieme limitato superiormente perché i suoi elementi sono compresi nell'intervallo (-∞,0). L'insieme è limitato superiormente con M=0, dove M=0 è il maggiorante più alto (estremo superiore). E' invece illimitato inferiormente perché non esiste alcun minorante e l'estremo inferiore è -∞.
Se l'insieme non è limitato superiormente, l'estremo superiore dell'insieme è più infinito (+∞).
$$ sup(A) = +∞ \Leftrightarrow \forall \: L \in R \: \exists \: a \in A \::\: a > L $$
E così via.
