Derivata di un versore
Cos'è la derivata di un versore
La derivata di un versore (u) è un vettore (v) perpendicolare al versore stesso. $$ \frac{d \vec{u}}{dt} = \vec{v} \ \ \ con \ \ \ \vec{v} \perp \vec{u} $$
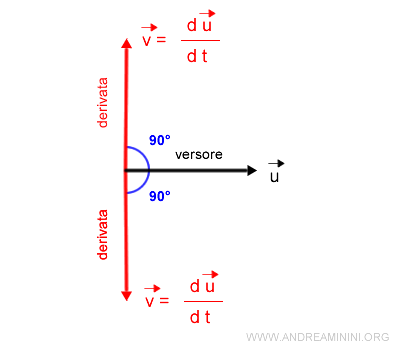
Dato un qualsiasi versore u, la sua derivata è un vettore ortogonale al versore stesso, ossia un vettore che forma un angolo di 90° rispetto al versore u.
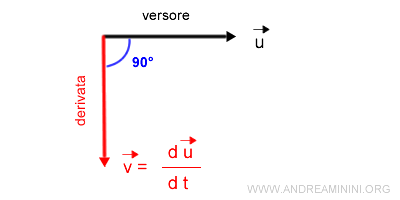
La derivata del versore si trova sulla direzione normale rispetto al versore, in un verso o nell'altro.
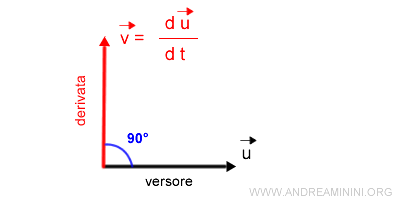
Nota. Nella dimostrazione che segue spiego tutti i passaggi di calcolo che spiegano questa affermazione. Per capirla è necessario conoscere il prodotto scalare tra due vettori.
Dimostrazione
Considero un versore qualsiasi
$$ \vec{u} $$
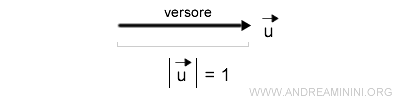
Un versore è un vettore con lunghezza unitaria ossia con modulo pari a 1.
Nota. Un versore può avere qualsiasi direzione o verso. In questa dimostrazione utilizzo la direzione parallela alle ascisse per mettere meglio in evidenza gli angoli.
Calcolo il prodotto scalare del versore per se stesso.
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos \alpha $$
Dove |u| è il modulo del versore e alfa è l'angolo formato dai due vettori del prodotto scalare.
In questo caso il prodotto scalare è tra due vettori che hanno la stessa direzione, il versore u per se stesso.
Quindi l'angolo alfa è zero.
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos 0 $$
Il coseno di zero è cos(0)=1 pari a uno.
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot 1 $$
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| $$
Un versore è un vettore con modulo unitario.
Pertanto, il modulo di u è pari a uno, ossia |u|=1.
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| $$
$$ \vec{u} \cdot \vec{u} = 1 \cdot 1 $$
Quindi, il prodotto scalare del versore per se stesso è pari a uno.
$$ \vec{u} \cdot \vec{u} = 1 $$
A questo punto calcolo la derivata del prodotto scalare del versore per se stesso rispetto al tempo.
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} $$
Sapendo che il prodotto scalare è 1, l'operazione si riduce alla derivata di una costante che notoriamente è pari a zero.
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d (1) }{dt} = 0 $$
D'altra parte posso anche calcolare la derivata del prodotto scalare tramite la regola della derivata di un prodotto.
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt}
$$
Questa derivata è equivalente alla precedente d(1)/dt=0, quindi ha lo stesso risultato, ossia è pari a zero.
$$ \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt} = 0 $$
La somma è tra due termini uguali, quindi posso anche scrivere.
$$ 2 (\frac{d \vec{u} }{dt} \cdot \vec{u} ) = 0 $$
Il primo fattore è un numero positivo (2) mentre il secondo è un'incognita.
Sapendo che il risultato è zero, il secondo fattore deve essere necessariamente pari a zero.
$$ \frac{d \vec{u} }{dt} \cdot \vec{u} = 0 $$
Ne consegue che il prodotto scalare tra la derivata del versore e il versore stesso è nullo.
Il prodotto scalare è nullo quando i vettori sono vettori ortogonali ossia formano un angolo di 90°.
Pertanto, la derivata del versore du/dt è un vettore ortogonale al versore stesso.
$$ \frac{d \vec{u} }{dt} \perp \vec{u} $$
Questo vuol dire che la derivata del versore si trova sulla direzione normale rispetto al versore.
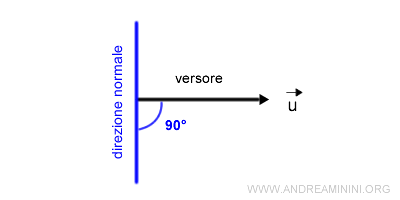
Può trovarsi sia sulla normale esterna che sulla normale interna.
E così via.
