Le componenti della velocità
Le componenti della velocità sono le derivate dei moti componenti rispetto al tempo $$ v_x = \frac{d \: x(t) }{d \: t} $$ $$ v_y = \frac{d \: y(t) }{d \: t} $$ $$ v_z = \frac{d \: z(t) }{d \: t} $$
Ogni componente della velocità è indipendente dalle altre.
Dimostrazione e spiegazione
La velocità istantanea è uguale alla derivata del raggio vettore di un punto materiale in movimento.
$$ \vec{v} = \frac{d \vec{r}}{d \: t} $$
Nello spazio il raggio vettore è composto dalla combinazione lineare dei moti componenti x(t), y(t), z(t) con i rispettivi versori degli assi x, y, z.
$$ \vec{r} = x(t) \hat{i} + y(t) \hat{j} + z(t) \hat{k} $$
Ecco la rappresentazione grafica di un vettore nello spazio a tre dimensioni.

Nota. I versori sono i vettori unitari e ortogonali tra loro che determinano la direzione e il verso degli assi cartesiani. Generalmente sono i versori $$ \hat{i} = (1,0,0) \\ \hat{j} = (0,1,0) \\ \hat{k} = (0,0,1) $$
Sostituisco la combinazione lineare del vettore nella derivata rispetto al tempo.
$$ \vec{v} = \frac{d \vec{r}}{d \: t} = \frac{d \: [ x(t) \hat{i} + y(t) \hat{j} + z(t) \hat{k} ]}{d \: t} $$
Poi scompongo nella somma delle derivate dei moti componenti.
Posso farlo perché la derivata è un operatore lineare.
$$ \vec{v} = \frac{d \: x(t) \hat{i}}{d \: t} + \frac{d \: y(t) \hat{j}}{d \: t} + \frac{d \: z(t) \hat{k}}{d \: t} $$
I versori i, j, k sono costanti indipendenti dal tempo, quindi escono dalle singole derivate
$$ \vec{v} = \frac{d \: x(t) }{d \: t} \hat{i} + \frac{d \: y(t) }{d \: t} \hat{j} + \frac{d \: z(t) }{d \: t} \hat{k} $$
A sua volta anche il vettore velocità v è un vettore.
Quindi posso scomporlo nelle componenti scalari vx, vy, vz moltiplicate per i versori degli assi.
$$ \vec{v} = v_x \hat{i} + v_y \hat{j} + v_z \hat{k} $$
Sostituisco v al primo membro dell'equazione e ottengo
$$ \vec{v} = \frac{d \: x(t) }{d \: t} \hat{i} + \frac{d \: y(t) }{d \: t} \hat{j} + \frac{d \: z(t) }{d \: t} \hat{k} $$
$$ v_x \hat{i} + v_y \hat{j} + v_z \hat{k} = \frac{d \: x(t) }{d \: t} \hat{i} + \frac{d \: y(t) }{d \: t} \hat{j} + \frac{d \: z(t) }{d \: t} \hat{k} $$
Poiché la scomposizione è la stessa sia nel membro di sinistra e sia di destra, ne consegue che vx deve essere uguale alla derivata dx(t)/dt, vy a dy(t)/dt e vz a dz(t)/dt.
Ho così trovato le componenti della velocità.
$$ v_x = \frac{d \: x(t) }{d \: t} $$
$$ v_y = \frac{d \: y(t) }{d \: t} $$
$$ v_z = \frac{d \: z(t) }{d \: t} $$
Le componenti della velocità misurano la velocità dello spostamento (moto rettilineo) della proiezione del corpo sugli assi cartesiani x, y, z.
In pratica, scompongono la velocità del moto nello spazio nelle velocità dei moti rettilinei sugli assi.
Esempio. Per semplicità rappresento il vettore velocità di un punto sul piano. Il punto è identificato dal raggio vettore mentre il vettore spostamento misura la velocità istantanea del punto sulla traiettoria nell'istante t. Il raggio vettore è tangente alla traiettoria.
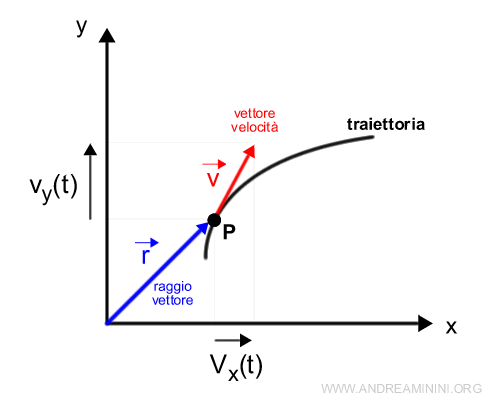
Pertanto, posso riscrivere il vettore velocità come somma delle velocità componenti del punto rispetto agli assi cartesiani x, y, z
$$ \vec{v} = v_x \hat{i} + v_y \hat{j} + v_z \hat{k} $$
Quest'ultima forma facilita il calcolo della velocità a partire dai moti componenti (coordinate cartesiane) del corpo nell'istante t.
Un esempio pratico
Ho i seguenti moti componenti
$$ x(t) = 3t+5 $$
$$ y(t) = 4t+3 $$
$$ y(t) = -6 $$
Posso calcolare la velocità del corpo tramite le componenti della velocità che, a loro volta, sono uguali alle derivate dei moti componenti.
$$ v_x = \frac{d \: x(t) }{d \: t} = \frac{d \: (3t+5) }{d \: t} = 3 $$
$$ v_y = \frac{d \: y(t) }{d \: t} = \frac{d \: (4t+3) }{d \: t} = 4 $$
$$ v_z = \frac{d \: z(t) }{d \: t} = \frac{d \: (-6) }{d \: t} = 0 $$
Quindi, nello spazio il vettore velocità ha componenti (3,4,0).
Per semplicità rappresento il vettore sul piano essendo a zero la velocità sull'asse z.
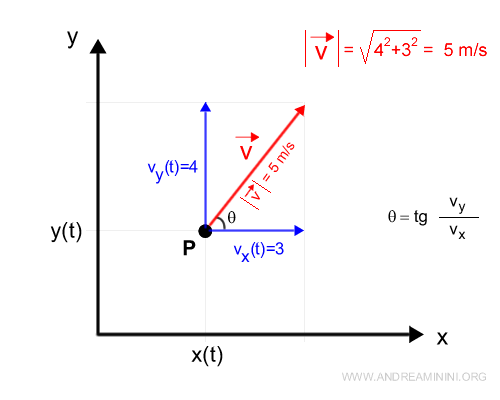
Il modulo del vettore velocità, ossia la lunghezza del vettore, è uguale alla velocità istantanea del corpo.
Per calcolare il modulo del vettore uso il teorema di Pitagora.
$$ |\vec{v}| = \sqrt{v_x^2+v_y^2+v_z^2} = \sqrt{3^2+4^2+0^2} = \sqrt{25} = 5 \: m/s $$
Nota. Il rapporto vy/vx è uguale alla tangente dell'angolo θ del vettore velocità rispetto all'asse x.
Ho così trovato la velocità istantanea (grandezza scalare) del punto P nell'istante t a partire dalla grandezza vettoriale
$$ v = 5 \: m/s $$
Nota. Se non dichiarato diversamente, in fisica l'unità di misura della velocità è sempre metri per secondo (m/s).
La direzione e il verso della velocità sono invece indicate nel vettore velocità.
E così via.
